Pramod's Blog
Evolution of LLMs

Evolution of LLMs

June 21, 2025

Table of Contents

The landscape of language models(LMs) has evolved dramatically since the introduction of the Transformer architecture in 2017. Here we will explore the

  • mathematical foundations
  • architectural innovations
  • training breakthroughs

We will talk about everything the code, math, and ideas that revolutionized NLP.

Additionally you can treat this blog as a sort of part 2, to my original blog on transformers which you can checkout here.

How this blog is structured

We will go year by year, going through the revolutionary ideas introduced by each paper.

In the beginning of each section, I have added the abstract, as well as the authors. I have done this to show you, the people were involved behind each idea. As well as what they felt like was the main contribution of their paper.

Below that I have provided the link to the original paper as well as my own implementation of it, subsequently there is a quick summary section which you can skim over if you feel like you know the crux behind the idea.

Note: All the quick summaries are AI generated, and may contain some mistakes. The core content is all human generated though, so it definitely contains mistakes :)

After that, each section contains intuition, code, and mathematical explanation (wherever required) for each idea. I have tried to add all the prerequisite knowledge wherever possible (Like the PPO section contains derivation of policy gradient methods, as well as explanation for TRPO). I have provided links to resources wherever I have felt I cannot provide enough background or do sufficient justice to the source material.

Additionally there has been a lot of innovation in vision modeling, TTS, Image gen, Video gen etc each of which deserves it’s own blog(And there will be!! I promise you that). As this is primarily an LLM blog, I will just give quick intro and links to some ground breaking innovations involving other ML papers.

Note: Do not take for granted all the hardware, data and benchmark innovations. Though I will briefly mention them. I implore you to explore them further if they interest you. This blog is strictly restricted to breakthroughs in Large Language Models, and mostly open source one’s. Even though current models by OpenAI, Anthropic, Google etc are amazing, not much is known about them to the public. So we will only briefly talk about them.

The AI timeline

This is a timeline of the most influential work. To read about more architectures that were huge at the time but died down eventually, consider going through the Transformer catalog.

The blog “Transformer models: an introduction and catalog — 2023 Edition” helped me immensely while making the timeline. Additionally this blog was helpful too.

Links post 2019 are broken as it’s still work in progress
2017
2018
2019
2020
2021
2022
2023
2024
2025


Note: I am releasing this blog early as a preview to get feedback from the community. It is still a work in progress and I plan to explain as well as implement each paper from each year. Do let me know your thoughts through my socials, or in the comments below!!!

2017: The Foundation Year

Transformer

Image of attention is all you need abstract

Link to paper: Attention is all you need
Link to implementation: [WORK IN PROGRESS]

Quick Summary

This is the famous “Attention Is All You Need” paper by Vaswani et al. that introduced the Transformer architecture - a groundbreaking neural network model that revolutionized natural language processing.

Key Innovation

The paper proposes replacing traditional recurrent neural networks (RNNs) and convolutional networks with a model based entirely on attention mechanisms. The core insight is that self-attention can capture dependencies between words regardless of their distance in a sequence, without needing to process them sequentially.

Architecture Highlights

  • Encoder-Decoder Structure: 6 layers each, with multi-head self-attention and feed-forward networks
  • Multi-Head Attention: Uses 8 parallel attention heads to capture different types of relationships
  • Positional Encoding: Sine/cosine functions to inject sequence order information
  • No Recurrence: Enables much better parallelization during training

Results The Transformer achieved state-of-the-art performance on machine translation tasks:

  • 28.4 BLEU on English-to-German (WMT 2014)
  • 41.8 BLEU on English-to-French
  • Trained significantly faster than previous models (12 hours vs. days/weeks)

Impact This architecture became the foundation for modern language models like BERT, GPT, and others. The paper’s core principle - that attention mechanisms alone are sufficient for high-quality sequence modeling - fundamentally changed how we approach NLP tasks.

The work demonstrated superior performance while being more parallelizable and interpretable than previous sequence-to-sequence models.


THE foundational paper that introduced some key ideas such as:

  • Scaled dot-product attention
  • Multi-head attention mechanism
  • Positional encodings
  • Layer normalization
  • Masked attention for autoregressive models

We have talked deeply about each of these topics previously and I implore you to check that part out here.

Problem

Sequential models like RNNs and LSTMs process text word-by-word, creating a fundamental bottleneck: each word must wait for the previous word to be processed. This sequential nature makes training painfully slow and prevents the model from understanding long-range dependencies effectively.

For example, in the sentence “The cat that lived in the house with the red door was hungry”, by the time the model reaches “was hungry”, it has largely forgotten about “The cat” due to the vanishing gradient problem. The model struggles to connect distant but related words.

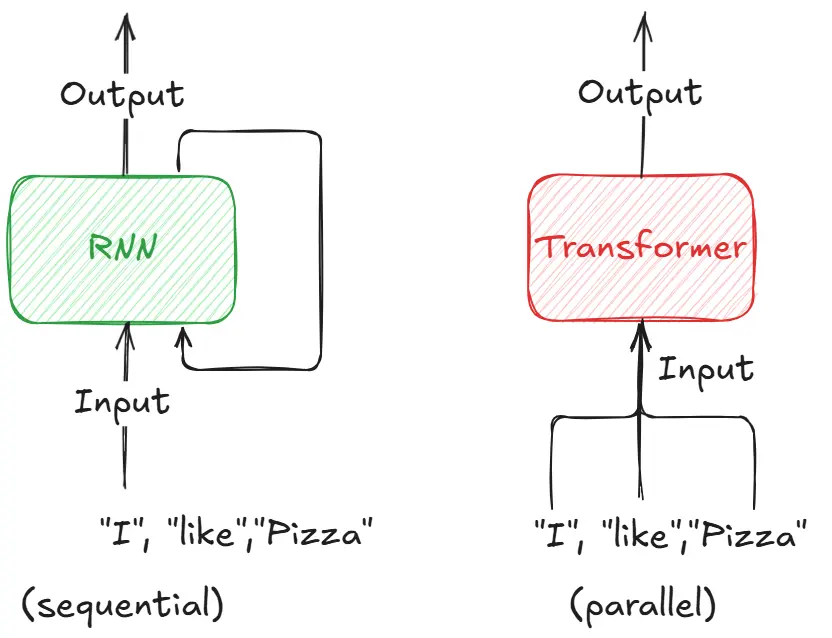
Image of rnn vs transformers

Solution

The Transformer replaced sequential processing with parallel attention mechanisms. Instead of processing words one-by-one, it looks at all words simultaneously and uses attention to determine which words are most relevant to each other, regardless of their distance in the sentence.

This attention-based approach allows the model to directly connect “The cat” with “was hungry” in a single step, while also enabling massive parallelization during training - turning what used to take weeks into hours.

Training a Transformer

This is one topic that we didn’t talk about extensively so let’s go over it, because that is where the true beauty of GPT lies. How to train over huge amounts of data.

We will build iteratively, first starting small. And going massive as we approach the GPT paper.

This blog helped me with this section.

Preparing the data

The original Transformer was trained for neural machine translation using English-German sentence pairs. The data preparation involves several crucial steps:

# Data preparation
import torch
from torch.utils.data import DataLoader, Dataset
from torch.nn.utils.rnn import pad_sequence

def prepare_training_data(sentences):
    # 1. Add special tokens
    processed_sentences = []
    for sentence in sentences:
        processed_sentences.append("<START> " + sentence + " <EOS>")

    # 2. Create vocabulary
    vocab = build_vocab(processed_sentences)
    vocab_size = len(vocab)

    # 3. Convert to tensor sequences
    sequences = []
    for sentence in processed_sentences:
        tokens = sentence.split()
        sequence = torch.tensor([vocab[token] for token in tokens])
        sequences.append(sequence)

    # 4. Pad sequences
    padded_sequences = pad_sequence(sequences, batch_first=True, padding_value=0)

    return padded_sequences, vocab_size

  1. Special tokens (<START> and <EOS>): These tell the model where sentences begin and end. The <START> token signals the decoder to begin generation, while <EOS> teaches it when to stop. Without these, the model wouldn’t know sentence boundaries. As we will move through the years, we will see how the special tokens used in LLMs have evolved as well. For example, think what will happen inside an LLM when it encounters a token that it hasn’t seen during training, like a chinese character etc.

  2. Vocabulary creation: The vocabulary maps every unique word/token in the training data to a number. This is how we convert text (which computers can’t process) into numerical tensors (which they can). The vocabulary size determines the final layer dimension of our model.

  3. Tensor conversion: Neural networks work with numbers, not words. Each word gets replaced by its vocabulary index, creating sequences of integers that can be fed into the model.

  4. Padding: Sentences have different lengths, but neural networks need fixed-size inputs for batch processing. Padding with zeros makes all sequences the same length, enabling efficient parallel computation.

Key Training Innovations

The Transformer introduced several training techniques that became standard:

Teacher Forcing with Masking

# During training, decoder sees target sequence shifted by one position
encoder_input = source_sequence
decoder_input = target_sequence[:, :-1]  # Remove last token
decoder_output = target_sequence[:, 1:]  # Remove first token

# Look-ahead mask prevents seeing future tokens
def create_look_ahead_mask(seq_len):
    mask = torch.triu(torch.ones(seq_len, seq_len), diagonal=1)
    return mask.bool()

mask = create_look_ahead_mask(decoder_input.size(1))

Why this works: Teacher forcing trains the decoder to predict the next token given all previous tokens, without requiring separate training data. The input-output shift creates a “next token prediction” task from translation pairs. The look-ahead mask ensures the model can’t “cheat” by seeing future tokens during training - it must learn to predict based only on past context, just like during real inference.

Custom Learning Rate Schedule The paper introduced a specific learning rate scheduler that warms up then decays:

# Learning rate schedule from the paper
import math

class TransformerLRScheduler:
    def __init__(self, optimizer, d_model=512, warmup_steps=4000):
        self.optimizer = optimizer
        self.d_model = d_model
        self.warmup_steps = warmup_steps
        self.step_count = 0

    def step(self):
        self.step_count += 1
        lr = self.get_lr()
        for param_group in self.optimizer.param_groups:
            param_group['lr'] = lr

    def get_lr(self):
        arg1 = self.step_count ** -0.5
        arg2 = self.step_count * (self.warmup_steps ** -1.5)
        return (self.d_model ** -0.5) * min(arg1, arg2)

Why this schedule: The warmup phase gradually increases the learning rate, preventing the model from making drastic weight updates early in training when gradients are noisy. After warmup, the learning rate decays proportionally to the square root of the step number, allowing for fine-tuning as training progresses. This schedule was crucial for training stability with the Transformer’s deep architecture.

Padding Masks for Loss Computation

import torch.nn.functional as F

def masked_loss(target, prediction, pad_token=0):
    # Don't compute loss on padding tokens
    mask = (target != pad_token).float()

    # Reshape for cross entropy
    prediction = prediction.view(-1, prediction.size(-1))
    target = target.view(-1)
    mask = mask.view(-1)

    # Compute cross entropy loss
    loss = F.cross_entropy(prediction, target, reduction='none')
    masked_loss = loss * mask

    return masked_loss.sum() / mask.sum()

Why masking matters: Padding tokens (zeros) are artificial - they don’t represent real words. Computing loss on them would teach the model incorrect patterns and waste computational resources. The mask ensures we only compute loss on actual content, leading to more meaningful gradients and better learning. This also prevents the model from learning to predict padding tokens, which would be useless during inference.

Training Configuration

The original paper used these hyperparameters:

  • Model size: 512 dimensions (base model)
  • Attention heads: 8
  • Encoder/Decoder layers: 6 each
  • Feed-forward dimension: 2048
  • Dropout: 0.1
  • Optimizer: Adam with custom learning rate schedule
  • Training time: ~12 hours on 8 P100 GPUs

The Training Loop

import torch
import torch.nn as nn
from torch.optim import Adam

def train_step(model, optimizer, scheduler, encoder_input, decoder_input, decoder_output):
    model.train()
    optimizer.zero_grad()

    # Forward pass
    prediction = model(encoder_input, decoder_input)

    # Compute masked loss and accuracy
    loss = masked_loss(decoder_output, prediction)
    accuracy = masked_accuracy(decoder_output, prediction)

    # Backward pass
    loss.backward()
    optimizer.step()
    scheduler.step()

    return loss.item(), accuracy.item()

# Main training loop
model = TransformerModel(src_vocab_size, tgt_vocab_size, d_model=512)
optimizer = Adam(model.parameters(), lr=1e-3, betas=(0.9, 0.98), eps=1e-9)
scheduler = TransformerLRScheduler(optimizer, d_model=512)

for epoch in range(num_epochs):
    for batch in dataloader:
        src_batch, tgt_batch = batch

        # Prepare inputs
        encoder_input = src_batch[:, 1:]     # Remove START token
        decoder_input = tgt_batch[:, :-1]    # Remove EOS token
        decoder_output = tgt_batch[:, 1:]    # Remove START token

        loss, accuracy = train_step(
            model, optimizer, scheduler,
            encoder_input, decoder_input, decoder_output
        )

        if step % 100 == 0:
            print(f'Epoch {epoch}, Step {step}, Loss: {loss:.4f}, Acc: {accuracy:.4f}')

Why This Training Approach Worked

  1. Parallelization: Unlike RNNs, all positions could be computed simultaneously
  2. Stable Gradients: Layer normalization and residual connections prevented vanishing gradients
  3. Efficient Attention: Scaled dot-product attention was computationally efficient
  4. Smart Masking: Prevented information leakage while enabling parallel training

This training methodology laid the groundwork for scaling to the massive language models we see today. The key insight was that with proper masking and attention mechanisms, you could train much larger models much faster than sequential architectures allowed.

While the original Transformer showed the power of attention-based training, it was still limited to translation tasks with paired data. The real revolution came when researchers realized they could use similar training techniques on massive amounts of unlabeled text data - setting the stage for GPT and the era of large language models.

RLHF - Reinforcement Learning from Human Preferences

Image of RLHF abstract

Link to paper: Deep reinforcement learning from human preferences
Link to implementation: [WORK IN PROGRESS]

Quick Summary

This paper presents a method for training reinforcement learning (RL) agents using human feedback instead of explicitly refined reward functions. Here’s a high-level overview:

The authors address a fundamental challenge in RL: for many complex tasks, designing appropriate reward functions is difficult or impossible. Instead of requiring engineers to craft these functions, they develop a system where:

  1. Humans compare short video clips of agent behavior (1-2 seconds)
  2. These comparisons train a reward predictor model
  3. The agent optimizes its policy using this learned reward function

Key contributions:

  • They show this approach can solve complex RL tasks using feedback on less than 1% of the agent’s interactions
  • This dramatically reduces the human oversight required, making it practical for state-of-the-art RL systems
  • They demonstrate training novel behaviors with just about an hour of human time
  • Their approach works across domains including Atari games and simulated robot locomotion

The technique represents a significant advance in aligning AI systems with human preferences, addressing concerns about misalignment between AI objectives and human values. By having humans evaluate agent behavior directly, the system learns rewards that better capture what humans actually want.


As mind boggling as it sounds, the famed algorithm RLHF came out in 2017, the same year attention is all you need came out. Let us understand the ideas put forth and why it was such a big deal.

(If you are not familiar with the idea of RL, I will recommend checking this small course by HuggingFace out)

Problem

Designing reward functions for complex behaviors is nearly impossible. How do you mathematically define “write a helpful response” or “be creative but truthful”? Traditional RL requires explicit numerical rewards for every action, but many desirable behaviors are subjective and context-dependent.

For example, it’s impossible to write code that scores joke quality, but humans can easily compare two jokes and say which is funnier.

Solution :

One possible solution is to allow a human to provide feedback on the agents’s current behavior and use this feedback to define the task. But this poses another problem, this would require hundreds of hours as well as domain experience. It was discovered by the researchers that preference modeling by a human even on a small subset provided great results.

An ideal solution will

  1. Enable us to solve tasks about which we can tell the desired behavior but not necessarily demonstrate or describe it.
  2. Allows systems to learn from non-expert users
  3. Scales to large problems
  4. Is economical

In their experiment, the researchers asked labellers to compare short video clips of the agent’s behavior. They found that by using a small sample of clips they were able to train the system to behave as desired.

Image of hop Image sourced from paper

The human observes the agent acting in the environment he then gives he’s feedback. Which is taken by reward predictor which numerical defines the reward. Which is sent to the RL algorithm this updates the agent based on the feedback and observation from the environment. That then changes the action of the agent.

Image of RLHF

This sounds simple enough in principle, but how do you teach a model to learn from these preferences. I.e reward modeling.

Note: We will be talking more in depth about RL algorithms in the next section. The topics in RL are rather complicated and usually talked in the end after an LLM is trained. So you can skip this part for now if it is daunting.

Reward predictor in RLHF

The following blogs helped me while writing this section

The reward predictor is trained to predict which of two given trajectories(σ¹, σ²) will be preferred by a human

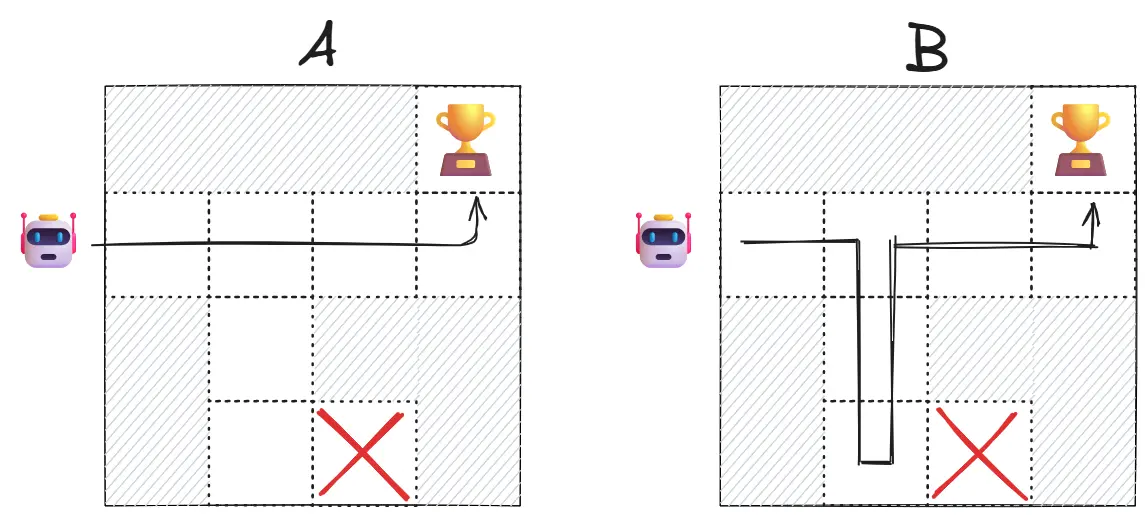
Example: Image of trajectories

Imagine two robot trajectories:

  • Trajectory A: Robot goes directly to the goal
  • Trajectory B: Robot roams around then goes to the goal

A human would prefer A (more efficient). The reward model learns to assign higher values to the observation-action pairs in trajectory A, eventually learning that “efficient movement” correlates with human preference.

Reward predictor equation

\[\hat{P}\left[\sigma^{1} \succ \sigma^{2}\right]=\frac{\exp \sum \hat{r}\left(o_{t}^{1}, a_{t}^{1}\right)}{\exp \sum \hat{r}\left(o_{t}^{1}, a_{t}^{1}\right)+\exp \sum \hat{r}\left(o_{t}^{2}, a_{t}^{2}\right)}\]

It is trained using cross-entropy loss to match human preferences:

\[\operatorname{loss}(\hat{r})=-\sum_{\left(\sigma^{1}, \sigma^{2}, \mu\right) \in D} \mu(1) \log \hat{P}\left[\sigma^{1} \succ \sigma^{2}\right]+\mu(2) \log \hat{P}\left[\sigma^{2} \succ \sigma^{1}\right]\]
Mathematical Notation
  • $\hat{P}\left[\sigma^{1} \succ \sigma^{2}\right]$: Predicted probability that trajectory segment $\sigma^{1}$ is preferred over trajectory segment $\sigma^{2}$
  • $\hat{r}$: The learned reward function
  • $o_{t}^{i}$: Observation at time $t$ in trajectory segment $i$
  • $a_{t}^{i}$: Action at time $t$ in trajectory segment $i$
  • $\sigma^{i}$: Trajectory segment $i$ (a sequence of observation-action pairs)
  • $\exp$: Exponential function
  • $\sum$: Summation over all timesteps in the trajectory segment
  • $\operatorname{loss}(\hat{r})$: Cross-entropy loss function for the reward model
  • $D$: Dataset of human preference comparisons
  • $\mu$: Distribution over ${1,2}$ indicating human preference
  • $\mu(1)$: Probability that human preferred segment 1
  • $\mu(2)$: Probability that human preferred segment 2
  • $\log$: Natural logarithm


Let us understand the Reward Function Fitting Process

The Preference-Predictor Model

The authors instead of directly creating a reward function (which rewards an agent when it does the desired behavior and punishes otherwise), they created a preference predictor. Which predicts which of the two given sequence of actions will be preferred by a human.

The Mathematical Formulation (Equation 1)

The equation P̂[σ¹ ≻ σ²] represents the predicted probability that a human would prefer trajectory segment σ¹ over segment σ².

Breaking down the formula:

  • $\sigma^{[1]}$ and $\sigma^{[2]}$ are two different trajectory segments (short video clips of agent behavior)
  • $o_{t}^{[i]}$ and $a_{t}^{[i]}$ represent the observation and action at time $t$ in trajectory $i$
  • $\hat{r}(o_{t}^{[i]}, a_{t}^{[i]})$ is the estimated reward for that observation-action pair
  • The formula uses the softmax function (exponential normalization):
\[\hat{P}\left[\sigma^{[1]} \succ \sigma^{[2]}\right] = \frac{\exp\left(\sum \hat{r}\left(o_{t}^{[1]}, a_{t}^{[1]}\right)\right)}{\exp\left(\sum \hat{r}\left(o_{t}^{[1]}, a_{t}^{[1]}\right)\right) + \exp\left(\sum \hat{r}\left(o_{t}^{[2]}, a_{t}^{[2]}\right)\right)}\]

This means:

  1. Sum up all the predicted rewards along trajectory 1
  2. Sum up all the predicted rewards along trajectory 2
  3. Apply exponential function to both sums
  4. The probability of preferring trajectory 1 is the ratio of exp(sum1) to the total exp(sum1) + exp(sum2)

The Loss Function

The goal is to find parameters for r̂ that make its predictions match the actual human preferences:

\[\operatorname{loss}(\hat{r}) = -\sum_{\left(\sigma^{[1]}, \sigma^{[2]}, \mu\right) \in D} \left[\mu([1])\log \hat{P}\left[\sigma^{[1]} \succ \sigma^{[2]}\right] + \mu([2])\log \hat{P}\left[\sigma^{[2]} \succ \sigma^{[1]}\right]\right]\]

Where:

  • $\left(\sigma^{[1]}, \sigma^{[2]}, \mu\right) \in D$ means we’re summing over all the comparison data in our dataset $D$
  • $\mu$ is a distribution over ${1,2}$ indicating which segment the human preferred
  • If the human strictly preferred segment 1, then $\mu([1]) = 1$ and $\mu([2]) = 0$
  • If the human strictly preferred segment 2, then $\mu([1]) = 0$ and $\mu([2]) = 1$
  • If the human found them equal, then $\mu([1]) = \mu([2]) = 0.5$

This is the standard cross-entropy loss function used in classification problems, measuring how well our predicted probabilities match the actual human judgments.

Consider reading this beautiful blog on Entropy by Christopher Olah, if you wish to gain a deeper understanding of cross-entropy.

The Bradley-Terry Model Connection

Note from Wikipedia: The Bradley–Terry model is a probability model for the outcome of pairwise comparisons between items, teams, or objects. Given a pair of items $i$ and $j$ drawn from some population, it estimates the probability that the pairwise comparison $i > j$ turns out true, as

\[\Pr(i>j) = \frac{p_i}{p_i + p_j}\]

where $p_i$ is a positive real-valued score assigned to individual $i$. The comparison $i > j$ can be read as “i is preferred to j”, “i ranks higher than j”, or “i beats j”, depending on the application.

This approach is based on the Bradley-Terry model, which is a statistical model for paired comparisons. It’s similar to:

  1. The Elo rating system in chess: Players have ratings, and the difference in ratings predicts the probability of one player beating another.

  2. In this case: Trajectory segments have “ratings” (the sum of rewards), and the difference in ratings predicts the probability of a human preferring one segment over another.

In essence, the reward function learns to assign higher values to states and actions that humans tend to prefer, creating a preference scale that can be used to guide the agent’s behavior.

The most important breakthrough: We can align AI systems with human values using comparative feedback from non-experts. This insight would prove crucial when training language models - instead of trying to define “helpful” or “harmless” mathematically, we can simply ask humans to compare outputs.

This comparative approach scales much better than rating individual responses, making it practical for training large language models on human preferences.

Fun story: One time researchers tried to RL a helicopter and it started flying backwards

PPO: Proximal Policy Optimization

Image of ppo abstract

Link to paper: Proximal Policy Optimization Algorithms
Link to implementation: [WORK IN PROGRESS]

Quick Summary

This paper by John Schulman et al. from OpenAI introduces Proximal Policy Optimization (PPO), a family of policy gradient methods for reinforcement learning that achieves the reliability and data efficiency of Trust Region Policy Optimization (TRPO) while being much simpler to implement and more compatible with various neural network architectures.

Key contributions:

  • A novel “clipped” surrogate objective function that provides a pessimistic estimate of policy performance
  • An algorithm that alternates between data collection and multiple epochs of optimization on the same data
  • Empirical validation showing PPO outperforms other online policy gradient methods across continuous control tasks and Atari games
  • A balance between sample complexity, implementation simplicity, and computation time

The core innovation is their clipped probability ratio approach, which constrains policy updates without requiring the complex second-order optimization techniques used in TRPO. This makes PPO more practical while maintaining performance guarantees.


Another LLM algo that came out in 2017, and that too again by OpenAI. Really goes to show how much they tried to advance AI and be public about it (At least in the early days).

This is going to be math heavy so be prepared (Dw, I will guide you in each step)

Problem

However, there is room for improvement in developing a method that is scalable (to large models and parallel implementations), data efficient, and robust (i.e., successful on a variety of problems without hyperparameter tuning). Q-learning (with function approximation) fails on many simple problems and is poorly understood, vanilla policy gradient methods have poor data effiency and robustness; and trust region policy optimization (TRPO) is relatively complicated, and is not compatible with architectures that include noise (such as dropout) or parameter sharing (between the policy and value function, or with auxiliary tasks).

Essentially there were a lot of RL algorithms, but none of them worked efficiently at scale.

Solution

This paper seeks to improve the current state of affairs by introducing an algorithm that attains the data efficiency and reliable performance of TRPO, while using only first-order optimization. We propose a novel objective with clipped probability ratios, which forms a pessimistic estimate (i.e., lower bound) of the performance of the policy. To optimize policies, we alternate between sampling data from the policy and performing several epochs of optimization on the sampled data

The authors found a way to take the best RL algorithm of the time (TRPO) and make it work at scale.

The following blogs & articles helped me write this section

What is Reinforcement Learning

Image of RL Image taken from HuggingFace Course

In RL we create an Agent (An ML model like Artificial Neural Network) give it a defined set of Actions $A_t$ (In this case it would be, move left, move right, Press A to shoot).

The agent then chooses an action and interacts with the Environment, which returns a new state as well as reward (positive if we survived or did a favourable outcome, negative if we die or do an unfavourable outcome).

Step by Step it looks something like this:

  • The agent recieves state $S_0$ from the environment (In this that would be the first frame of the game)
  • Based on state $S_0$, the agent takes action $A_0$ (chooses to move right)
  • The environment goes to new frame, new state $S_1$.
  • The environment gives the agent, reward $R_t$ (still alive!!!).

The idea behind RL is based on reward hypothesis, which states that

All goals can be described as the maximization of the expected return (expected cumulative reward)

Which can be mathematically represented as $R(\tau) = r_{t+1} + r_{t+2} + r_{t+3} + r_{t+4} + \ldots$ ($\tau$ read as tau)

Remember this, It will prove useful later.

Policy π: The Agent’s Brain

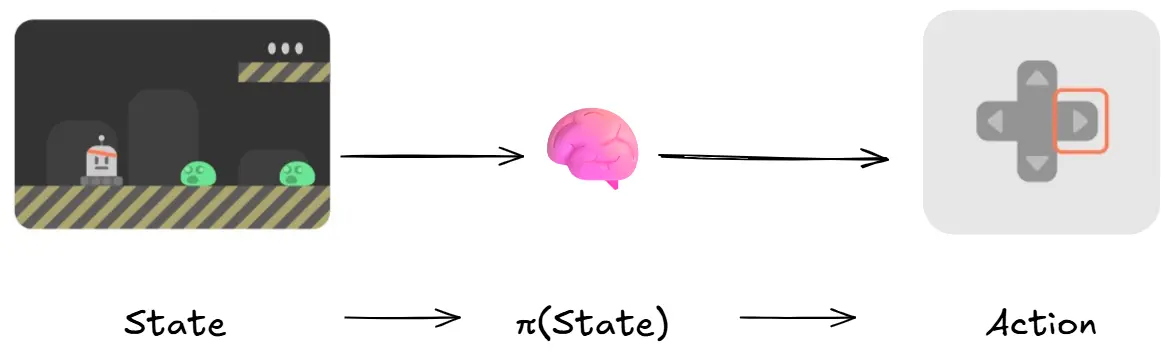
Image of policy based approach

The Policy π is the brain of our Agent, it’s the function that tells an Agent what action it should take at a given state and time.

The policy is what we want to train and make an optimum policy π*, that maximizes expected return when the agent acts according to it. (remember that is the idea behind RL)

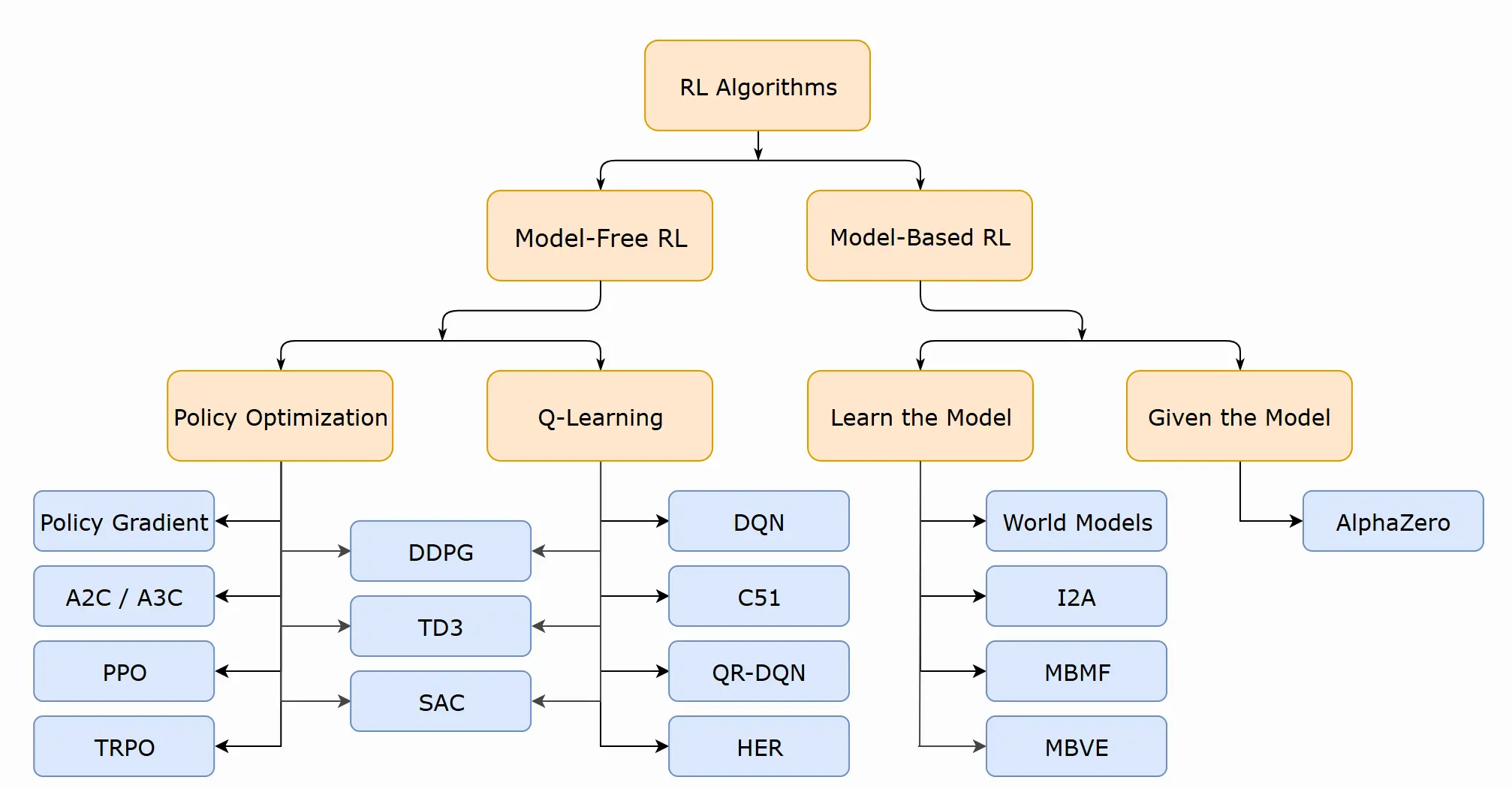Image of RL Image taken from OpenAI Spinning Up

There are many RL algorithms present that we can use to train the policy as you can see from the image above, But most of them are developed from two central methods:

  1. Policy based methods : Directly, by teaching the agent to learn which action to take, given the current state
  2. Value based methods : Indirectly, teach the agent to learn which state is more valuable and then take the action that leads to the more valuable states

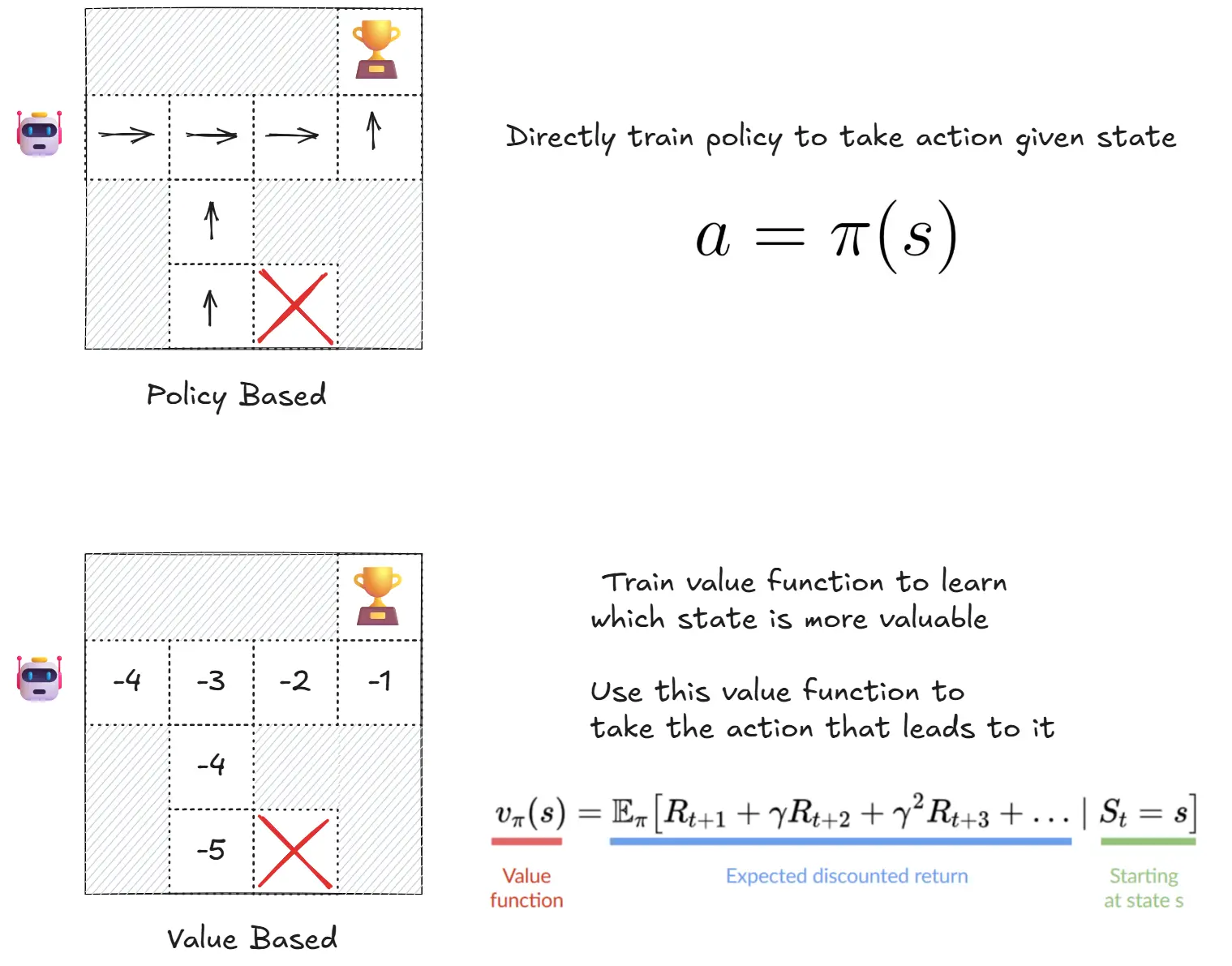Image of RL Image taken from HuggingFace Course

(Don’t get scared by the equations, I will explain them as we move forward. Also, this was a quick recap of RL, for a better deep dive. Consider going through the HF course)

As this section is dedicated to PPO, I will primarily be talking about the topics concerned with it. It can broadly be put in the following order:

  1. Policy Gradient Methods
  2. TRPO
  3. PPO

I am skipping over many other interesting and amazing algorithms like Q-Learning, DQN, Actor-critic etc. As they are not relevant to this section. I still implore you to explore them through the links I have provided to get a better, broader and deeper grasp of RL.

Before we move to the next section, I want to talk about a question that baffled me when I started learning about RL.

“Why do we need a value based approach”

Policy based approach seem to work great and are intuitive as well, given a state, choose an action. Then why do we use value based approaches. Needless complexity. Think for a minute then see the answer

Answer

Value-based methods shine in scenarios where policy-based methods struggle:

1. Discrete Action Spaces with Clear Optimal Actions In environments like Atari games or grid worlds, there’s often a single best action for each state. Value-based methods (like DQN) can directly learn which action has the highest expected return, making them sample-efficient for these deterministic scenarios.

2. Exploration Efficiency Value functions provide natural exploration strategies. Methods like ε-greedy or UCB can systematically explore based on value estimates. Policy methods often struggle with exploration, especially in sparse reward environments where random policy perturbations rarely discover good behavior.

3. Off-Policy Learning Value-based methods can learn from any data - even old experiences stored in replay buffers. This makes them incredibly sample-efficient. Policy methods traditionally required on-policy data, though modern techniques like importance sampling have bridged this gap.

4. Computational Efficiency In discrete action spaces, value-based methods often require just one forward pass to select an action (argmax over Q-values). Policy methods might need to sample from complex probability distributions or solve optimization problems.

Where Policy Methods Fail:

  • High-dimensional discrete actions: Computing argmax becomes intractable
  • Continuous control: You can’t enumerate all possible actions to find the maximum
  • Stochastic optimal policies: Sometimes the best strategy is inherently random (like rock-paper-scissors), which value methods can’t represent directly

The truth is, both approaches are complementary tools for different types of problems.


Policy Gradient Methods

Policy gradient methods directly optimize a policy function by adjusting its parameters in the direction of greater expected rewards. They work by:

  1. Collecting experience (state-action pairs and rewards) using the current policy
  2. Estimating the policy gradient (the direction that would improve the policy)
  3. Updating the policy parameters using this gradient

The Gradient Estimator

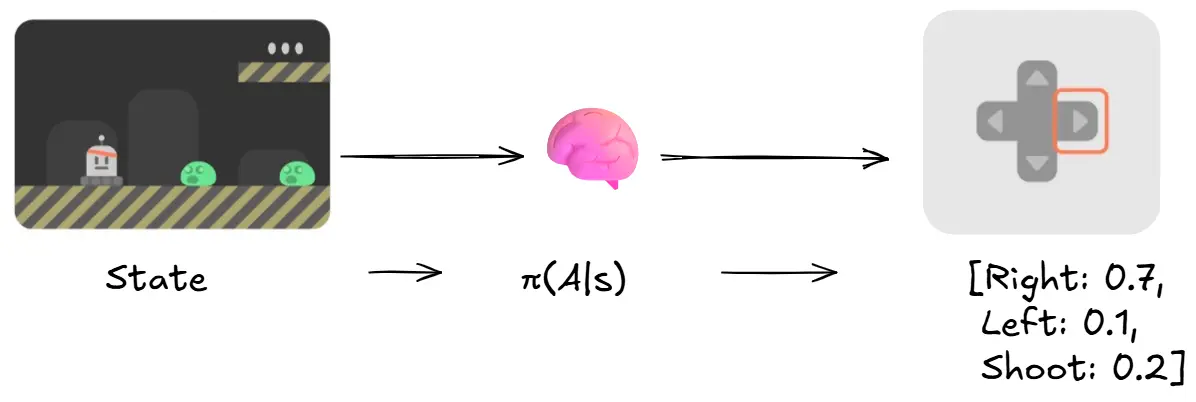
In our discussion so far, we talked about deterministic policy based methods. Ie given a state, choose an action $\pi(s) = a$. But when we are talking about policy gradients, we use a stochastic policy based method. Ie given a state, return a probability distribution of actions $\pi(a|s) = P[A|s]$.

Image of RL

We also need to be aware of a few terms and mathematical tricks before moving forward:

  1. Trajectory: A series of state action pair is called a trajectory.

    \[\tau = (s_1,a_1,s_2,a_2,\ldots,s_H,a_H)\]

  2. Log derivative trick:

    \[\nabla_\theta \log z = \frac{1}{z} \nabla_\theta z\]

    This trick allows us to convert the gradient of a probability into the gradient of its logarithm, which is computationally more stable and easier to work with.

    (To derive it just apply chain rule and know that the derivative of $\log(x)$ = $1/x$)

  3. Definition of Expectation:

    For discrete distributions: \(\mathbb{E}_{x \sim p(x)}[f(x)] = \sum_x p(x)f(x) \tag{1}\)

    For continuous distributions: \(\mathbb{E}_{x \sim p(x)}[f(x)] = \int_x p(x)f(x) \, dx \tag{2}\)

    If you are new to the idea of expectation, Consider checking this amazing blog on the topic.

Deriving the Policy Gradient

Let $\tau$ be a trajectory (sequence of state-action pairs), $\theta$ be the weights of our neural network policy. Our policy $\pi_\theta$ outputs action probabilities that depend upon the current state and network weights.

We begin with the reward hypothesis: we want to maximize $R(\tau)$ where $\tau$ is a trajectory.

We can write the objective as the probability of a trajectory being chosen by the policy multiplied by the reward for that trajectory:

\[J(\theta) = \mathbb{E}_{\tau \sim \pi_\theta}[R(\tau)] = \sum_\tau \pi_\theta(\tau)R(\tau)\]

This formulation is crucial because it connects:

  • $\pi_\theta(\tau)$: How likely our current policy is to generate trajectory $\tau$
  • $R(\tau)$: How much reward we get from that trajectory

For continuous trajectory spaces, we can write this as:

\[J(\theta) = \mathbb{E}_{\tau \sim \pi_\theta}[R(\tau)] = \int \pi_\theta(\tau)R(\tau)d\tau\]

Now we can derive the policy gradient by taking the gradient of our objective:

\[\nabla_\theta J(\theta) = \nabla_\theta \int \pi_\theta(\tau)R(\tau)d\tau \tag{3}\] \[= \int \nabla_\theta \pi_\theta(\tau)R(\tau)d\tau \tag{4}\] \[= \int \pi_\theta(\tau) \frac{\nabla_\theta \pi_\theta(\tau)}{\pi_\theta(\tau)} R(\tau)d\tau \tag{5}\] \[= \int \pi_\theta(\tau) \nabla_\theta \log \pi_\theta(\tau) R(\tau)d\tau \tag{6}\] \[= \mathbb{E}_{\tau \sim \pi_\theta}[\nabla_\theta \log \pi_\theta(\tau) R(\tau)] \tag{7}\]

Step-by-step explanation:

  • (3) Start with gradient of our objective function
  • (4) Push gradient inside the integral
  • (5) Multiply and divide by $\pi_\theta(\tau)$
  • (6) Apply the log derivative trick: $\nabla_\theta \log(z) = \frac{1}{z} \nabla_\theta z$
  • (7) Convert back to expectation form

The trajectory probability factors as: \(\pi_\theta(\tau) = \prod_{t=0}^{T} \pi_\theta(a_t|s_t)\)

So the log probability becomes: \(\log \pi_\theta(\tau) = \sum_{t=0}^{T} \log \pi_\theta(a_t|s_t)\)

What does this mean for us? If you want to maximize your expected reward, you can use gradient ascent. The gradient of the expected reward has an elegant form - it’s simply the expectation of the trajectory return times the sum of log probabilities of actions taken in that trajectory.

In reinforcement learning, a trajectory $\tau = (s_1, a_1, s_2, a_2, \ldots, s_T, a_T)$ is generated through a sequential process. The probability of observing this specific trajectory under policy $\pi_\theta$ comes from the chain rule of probability.

This is quite complex to intuitively understand in my opinion. Consider going through this stack exchange.

Intuition: Let’s calculate the joint probability of a sequence like $P(\text{sunny weather, white shirt, ice cream})$ - what’s the chance it’s sunny outside, I’m wearing a white shirt, and I chose to eat ice cream all happening together?

We can break this down step by step: First, what’s the probability it’s sunny outside? That’s $P(\text{sunny})$. Given that it’s sunny, what are the chances I wear a white shirt? That’s $P(\text{white shirt | sunny})$. Finally, given it’s sunny and I’m wearing white, what’s the probability I eat ice cream? That’s $P(\text{ice cream | sunny, white shirt})$.

\(P(\text{sunny, white shirt, ice cream}) = P(\text{sunny}) \cdot P(\text{white shirt | sunny}) \cdot P(\text{ice cream | sunny, white shirt})\)

By multiplying these conditional probabilities, we get the full joint probability. In reinforcement learning, trajectories work the same way: $P(s_1, a_1, s_2, a_2, \ldots)$ breaks down into “what state do we start in?” then “what action do we take?” then “where do we transition?” and so on. Each step depends only on what happened before, making complex trajectory probabilities manageable to compute and optimize.

The joint probability of a sequence of events can be factored as: \(P(s_1, a_1, s_2, a_2, \ldots, s_T, a_T) = P(s_1) \cdot P(a_1|s_1) \cdot P(s_2|s_1, a_1) \cdot P(a_2|s_1, a_1, s_2) \cdots\)

However, in the Markov Decision Process (MDP) setting, we have two key assumptions:

  1. Markov Property: Next state depends only on current state and action: $P(s_{t+1}|s_1, a_1, \ldots, s_t, a_t) = P(s_{t+1}|s_t, a_t)$
  2. Policy Markov Property: Action depends only on current state: $P(a_t|s_1, a_1, \ldots, s_t) = \pi_\theta(a_t|s_t)$
Chapter 3 of RL book by Sutton and Barto covers the topic well

Applying these assumptions:

\[\pi_\theta(\tau) = \pi_\theta(s_1, a_1, \ldots, s_T, a_T) = p(s_1) \prod_{t=1}^{T} \pi_\theta(a_t|s_t)p(s_{t+1}|s_t, a_t)\] \[\underbrace{p(s_1) \prod_{t=1}^{T} \pi_\theta(a_t|s_t)p(s_{t+1}|s_t, a_t)}_{\pi_\theta(\tau)}\]
  • $p(s_1)$: Initial state distribution (environment dependent)
  • $\pi_\theta(a_t|s_t)$: Policy probability of choosing action $a_t$ in state $s_t$
  • $p(s_{t+1}|s_t, a_t)$: Environment transition probability (environment dependent)

When we take the log of a product, it becomes a sum:

\[\log \pi_\theta(\tau) = \log p(s_1) + \sum_{t=1}^{T} \log \pi_\theta(a_t|s_t) + \sum_{t=1}^{T} \log p(s_{t+1}|s_t, a_t)\]

The first and last terms do not depend on $\theta$ and can be removed when taking gradients(and this is often done in practice):

  • $\log p(s_1)$: Initial state is determined by environment, not our policy
  • $\log p(s_{t+1}|s_t, a_t)$: Environment dynamics don’t depend on our policy parameters
\[\nabla_\theta \left[ \log p(s_1) + \sum_{t=1}^{T} \log \pi_\theta(a_t|s_t) + \sum_{t=1}^{T} \log p(s_{t+1}|s_t, a_t) \right]\] \[= \nabla_\theta \left[ \cancel{\log p(s_1)} + \sum_{t=1}^{T} \log \pi_\theta(a_t|s_t) + \cancel{\sum_{t=1}^{T} \log p(s_{t+1}|s_t, a_t)} \right]\]

Therefore: \(\nabla_\theta \log \pi_\theta(\tau) = \nabla_\theta \sum_{t=1}^{T} \log \pi_\theta(a_t|s_t) = \sum_{t=1}^{T} \nabla_\theta \log \pi_\theta(a_t|s_t)\)

So the policy gradient: \(\nabla_\theta J(\theta) = \mathbb{E}_{\tau \sim \pi_\theta}[\nabla_\theta \log \pi_\theta(\tau) R(\tau)]\)

becomes: \(\nabla_\theta J(\theta) = \mathbb{E}_{\tau \sim \pi_\theta}\left[\left(\sum_{t=1}^{T} \nabla_\theta \log \pi_\theta(a_t|s_t)\right) R(\tau)\right]\)

The trajectory return $R(\tau)$ is the total reward collected along the trajectory: \(R(\tau) = \sum_{t=1}^{T} r(s_t, a_t)\)

So our gradient becomes: \(\nabla_\theta J(\theta) = \mathbb{E}_{\tau \sim \pi_\theta}\left[\left(\sum_{t=1}^{T} \nabla_\theta \log \pi_\theta(a_t\|s_t)\right) \left(\sum_{t=1}^{T} r(s_t, a_t)\right)\right]\)

How do we compute expectations in practice?

We can’t compute the expectation $\mathbb{E}_{\tau \sim \pi{\theta}}[\cdot]$ analytically because:

  • There are infinitely many possible trajectories
  • We don’t know the environment dynamics $p(s_{t+1}|s_t, a_t)$

Instead, we use Monte Carlo sampling:

  1. Collect $N$ sample trajectories by running our current policy: ${\tau_1, \tau_2, \ldots, \tau_N}$
  2. Approximate the expectation using the sample average:
\[\mathbb{E}_{\tau \sim \pi_\theta}[f(\tau)] \approx \frac{1}{N} \sum_{i=1}^{N} f(\tau_i)\]

Applying Monte Carlo approximation

This is a fabulous video to understand Monte Carlo approximation.

Substituting our specific function: \(f(\tau) = \left(\sum_{t=1}^{T} \nabla_\theta \log \pi_\theta(a_t|s_t)\right) \left(\sum_{t=1}^{T} r(s_t, a_t)\right)\)

We get: \(\boxed{\nabla_\theta J(\theta) \approx \frac{1}{N} \sum_{i=1}^{N} \left(\sum_{t=1}^{T} \nabla_\theta \log \pi_\theta(a_{i,t}|s_{i,t})\right) \left(\sum_{t=1}^{T} r(s_{i,t}, a_{i,t})\right)}\)

\[\boxed{\theta \leftarrow \theta + \alpha \nabla_\theta J(\theta)}\]

Where:

  • $i$ indexes the sampled trajectories ($1$ to $N$)
  • $t$ indexes time steps within each trajectory ($1$ to $T$)
  • $(s_{i,t}, a_{i,t})$ is the state-action pair at time $t$ in trajectory $i$

The elegant result is that we only need gradients of our policy’s action probabilities - the environment dynamics completely disappear from our gradient computation! This makes policy gradients model-free and widely applicable.

And we use this policy gradient to update the policy $\theta$.

To get an intuition behind the idea consider reading the intuition part of this blog.

Policy Gradient for Continuous Space

So far, we’ve been working with discrete action spaces, like our super mad bot game where you can move left, move right, or press A to shoot. But what happens when your agent needs to control a robot arm, steer a car, or even select the “best” next token in language model fine-tuning? Welcome to the world of continuous control!

In discrete spaces, our policy outputs probabilities for each possible action:

  • Move left: 30%
  • Move right: 45%
  • Shoot: 25%

But in continuous spaces, actions are real numbers. Imagine trying to control a robot arm where the joint angle can be any value between -180° and +180°. You can’t enumerate probabilities for every possible angle, there are infinitely many! (like in real numbers, you cannot even count the numbers present between 179 and 180… Where do you even begin?)

The solution is to make our neural network output parameters of a probability distribution (eg mean and standard deviation of a normal distribution) instead of individual action probabilities. Specifically, we use a Gaussian (normal) distribution.

Here’s how it works:

Instead of: $\pi_\theta(a_t|s_t) = \text{[probability for each discrete action]}$
We use: $\pi_\theta(a_t|s_t) = \mathcal{N}(f_{\text{neural network}}(s_t); \Sigma)$

Let’s break it down:

  1. Feed the state $s_t$ into your neural network
  2. Network outputs the mean $\mu = f_{\text{neural network}}(s_t)$ - this is the “preferred” action
  3. Choose a covariance matrix $\Sigma$ - this controls how much exploration/uncertainty around that mean
  4. Sample the actual action from the Gaussian: $a_t \sim \mathcal{N}(\mu, \Sigma)$

Now comes the amazing part. Remember our policy gradient formula?

\[\nabla_\theta J(\theta) = \mathbb{E}_{\tau \sim \pi_\theta}\left[\left(\sum_{t=1}^{T} \nabla_\theta \log \pi_\theta(a_t|s_t)\right) R(\tau)\right]\]

The exact same formula still applies! We just need to compute $\nabla_\theta \log \pi_\theta(a_t|s_t)$ differently.

Let’s start with what a Multivariant Gaussian distribution actually looks like. For continuous actions, we assume they follow this probability density function:

\[f(x) = \frac{1}{(2\pi)^{d/2} |\Sigma|^{1/2}} \exp\left\{-\frac{1}{2}(x - \mu)^T \Sigma^{-1} (x - \mu)\right\}\]

This looks scary, but it’s just the mathematical way of saying: “actions are most likely to be near the mean $\mu$, with spread determined by covariance $\Sigma$.”

(To understand where this idea comes from, read 13.7 from RL by Sutton and Barton)

Now, since our policy $\pi_\theta(a_t|s_t) = \mathcal{N}(f_{\text{neural network}}(s_t); \Sigma)$, we have:

\[\log \pi_\theta(a_t|s_t) = \log f(a_t)\]

Taking the logarithm of our Gaussian:

\[\log \pi_\theta(a_t|s_t) = \log\left[\frac{1}{(2\pi)^{d/2} |\Sigma|^{1/2}} \exp\left\{-\frac{1}{2}(a_t - \mu)^T \Sigma^{-1} (a_t - \mu)\right\}\right]\]

Using properties of logarithms ($\log(AB) = \log A + \log B$ and $\log(e^x) = x$):

\[\log \pi_\theta(a_t|s_t) = \log\left[\frac{1}{(2\pi)^{d/2} |\Sigma|^{1/2}}\right] - \frac{1}{2}(a_t - \mu)^T \Sigma^{-1} (a_t - \mu)\]

The first term is just a constant (doesn’t depend on our neural network parameters $\theta$), so we can ignore it when taking gradients:

\[\log \pi_\theta(a_t|s_t) = -\frac{1}{2}(a_t - \mu)^T \Sigma^{-1} (a_t - \mu) + \text{const}\]

Since $\mu = f_{\text{neural network}}(s_t)$, we can rewrite this as:

\[\log \pi_\theta(a_t|s_t) = -\frac{1}{2}||f(s_t) - a_t||^2_\Sigma + \text{const}\]

Both the above equations are the same, it’s just a shorthand of writing it this way. It is also known as Mahalanobis distance squared.

Now we can compute the gradient with respect to our network parameters $\theta$:

\[\nabla_\theta \log \pi_\theta(a_t|s_t) = \nabla_\theta \left[-\frac{1}{2}(a_t - f(s_t))^T \Sigma^{-1} (a_t - f(s_t))\right]\]

Let’s define $u = a_t - f(s_t)$ to simplify notation. Our expression becomes:

\[\nabla_\theta \log \pi_\theta(a_t|s_t) = \nabla_\theta \left[-\frac{1}{2} u^T \Sigma^{-1} u\right]\]

Since $a_t$ and $\Sigma^{-1}$ don’t depend on $\theta$, we have:

\[\frac{\partial u}{\partial \theta} = \frac{\partial}{\partial \theta}(a_t - f(s_t)) = -\frac{\partial f(s_t)}{\partial \theta}\]

For the quadratic form $u^T \Sigma^{-1} u$, using the chain rule:

\[\frac{\partial}{\partial \theta}(u^T \Sigma^{-1} u) = \frac{\partial u^T}{\partial \theta} \Sigma^{-1} u + u^T \Sigma^{-1} \frac{\partial u}{\partial \theta}\]

Since $\Sigma^{-1}$ is symmetric, we can write:

\[\frac{\partial}{\partial \theta}(u^T \Sigma^{-1} u) = 2 u^T \Sigma^{-1} \frac{\partial u}{\partial \theta}\]

Substituting back our expressions:

\[\nabla_\theta \log \pi_\theta(a_t|s_t) = -\frac{1}{2} \cdot 2 \cdot u^T \Sigma^{-1} \frac{\partial u}{\partial \theta}\] \[= -u^T \Sigma^{-1} \left(-\frac{\partial f(s_t)}{\partial \theta}\right)\] \[= u^T \Sigma^{-1} \frac{\partial f(s_t)}{\partial \theta}\]

Substituting $u = a_t - f(s_t)$ back:

\[\nabla_\theta \log \pi_\theta(a_t|s_t) = (a_t - f(s_t))^T \Sigma^{-1} \frac{\partial f(s_t)}{\partial \theta}\]

Since $\Sigma^{-1}$ is symmetric, $(a_t - f(s_t))^T \Sigma^{-1} = \Sigma^{-1}(a_t - f(s_t))$ when treated as a row vector, so we can write:

\[\nabla_\theta \log \pi_\theta(a_t|s_t) = \Sigma^{-1}(a_t - f(s_t)) \frac{\partial f(s_t)}{\partial \theta}\]

Rearranging to match the original form:

\[\nabla_\theta \log \pi_\theta(a_t|s_t) = -\Sigma^{-1}(f(s_t) - a_t) \frac{\partial f(s_t)}{\partial \theta}\]

This gradient has a beautiful intuitive interpretation:

  • $(f(s_t) - a_t)$: The difference between what your network predicted and the action you actually took
  • $\frac{df}{d\theta}$: How to change the network parameters to affect the output
  • $\Sigma^{-1}$: Weighting factor (less weight for high-variance directions)

When you collect experience and compute rewards, here’s what happens:

  1. Good action taken ($R(\tau) > 0$): The gradient pushes $f(s_t)$ closer to the good action $a_t$
  2. Bad action taken ($R(\tau) < 0$): The gradient pushes $f(s_t)$ away from the bad action $a_t$
  3. Standard backpropagation: This gradient flows back through the network to update $\theta$

Our policy gradient update remains: \(\theta \leftarrow \theta + \alpha \nabla_\theta J(\theta)\)

The only difference is how we compute $\nabla_\theta \log \pi_\theta(a_t|s_t)$:

  • Discrete case: Gradient of softmax probabilities
  • Continuous case: Gradient of Gaussian log-likelihood (what we just derived!)

Everything else stays identical - collect trajectories, compute returns, update parameters. The same core algorithm seamlessly handles both discrete and continuous control problems!

Policy Gradient Improvements

There are two methods in which RL is trained

  1. Monte Carlo Learning: Cummulative reward of the entire episode (Entire run of the enviorment)
  2. Temporal Difference Learning: Reward is used to update policy in every step

Image of MC vs TD Image taken from Reinforcement Learning and Bandits for Speech and Language Processing: Tutorial, Review and Outlook

Policy Gradient (PG) uses MC this causes it to have low bias (Expected reward is close to actual reward, as the same policy is used throughout the run) but high variance (Some runs produce great results, some really bad).

A stack exchange on bias & variance in RL

Remember, our policy gradient formula is:

\[\nabla_\theta J(\theta) \approx \frac{1}{N} \sum_{i=1}^{N} \left(\sum_{t=1}^{T} \nabla_\theta \log \pi_\theta(a_{i,t}|s_{i,t})\right) \left(\sum_{t=1}^{T} r(s_{i,t}, a_{i,t})\right)\]

We can rewrite this more compactly as:

\[\nabla_\theta J(\theta) \approx \frac{1}{N} \sum_{i=1}^{N} \sum_{t=1}^{T} \nabla_\theta \log \pi_\theta(a_{i,t}|s_{i,t}) \cdot Q(s_{i,t}, a_{i,t})\]

Where $Q(s,a)$ represents the total reward we get from taking action $a$ in state $s$ (this is called the Q-function or action-value function).

The Baseline Trick

Here’s a mathematical insight: we can subtract any term from our gradient as long as that term doesn’t depend on our policy parameters $\theta$.

Why? Because: \(\nabla_\theta [f(\theta) - c] = \nabla_\theta f(\theta) - \nabla_\theta c = \nabla_\theta f(\theta) - 0 = \nabla_\theta f(\theta)\)

So instead of using $Q(s,a)$ directly, we can use $Q(s,a) - V(s)$, where $V(s)$ is some baseline function.

The most natural choice for baseline is $V(s) =$ the expected reward from state $s$ (The value function). This represents “how good is this state on average?”

Our new gradient becomes: \(\nabla_\theta J(\theta) \approx \frac{1}{N} \sum_{i=1}^{N} \sum_{t=1}^{T} \nabla_\theta \log \pi_\theta(a_{i,t}|s_{i,t}) \cdot (Q(s_{i,t}, a_{i,t}) - V(s_{i,t}))\)

This is defined as the Advantage Function: \(A^{\pi}(s,a) = Q^{\pi}(s,a) - V^{\pi}(s)\)

The advantage function answers the question: “How much better is taking action $a$ in state $s$ compared to the average action in that state?”

  • $A(s,a) > 0$: Action $a$ is better than average → increase its probability
  • $A(s,a) < 0$: Action $a$ is worse than average → decrease its probability
  • $A(s,a) = 0$: Action $a$ is exactly average → no change needed

Our final policy gradient becomes: \(\boxed{\nabla_\theta J(\theta) \approx \frac{1}{N} \sum_{i=1}^{N} \sum_{t=1}^{T} \nabla_\theta \log \pi_\theta(a_{i,t}|s_{i,t}) \cdot A^{\pi}(s_{i,t}, a_{i,t})}\)

Let’s understand why this reduces variance with an example:

Situation 1: Trajectory A gets +10 rewards, Trajectory B gets -10 rewards

  • If average performance is 0: $A_A = +10$, $A_B = -10$
  • Result: Increase A’s probability, decrease B’s probability ✓

Situation 2: Trajectory A gets +10 rewards, Trajectory B gets +1 rewards

  • If average performance is +5.5: $A_A = +4.5$, $A_B = -4.5$
  • Result: Increase A’s probability, decrease B’s probability ✓

Even when both trajectories have positive rewards, the advantage function correctly identifies which one is relatively better!

In deep learning, we want input features to be zero-centered. The advantage function does exactly this for our rewards:

  • Without baseline: All positive rewards → always increase probabilities
  • With advantage: Rewards centered around zero → increase good actions, decrease bad ones

This gives our policy gradient much clearer, less conflicting signals, significantly reducing variance and improving convergence.

Vanilla Policy Gradient Algorithm

Now that we understand the advantage function, let’s see how it all comes together in the complete algorithm:

\[\nabla U(\theta) \approx \hat{g} = \frac{1}{m} \sum_{i=1}^{m} \nabla_\theta \log P(\tau^{(i)}; \theta)(R(\tau^{(i)}) - b)\]

(The notation may change from paper to paper, but the core idea remains the same)

Image of policy based approach Image taken from RL — Policy Gradient Explained

Reward Discount

There’s one more important technique that further reduces variance: reward discounting.

Reward discount reduces variance by reducing the impact of distant actions. The intuition is that actions taken now should have more influence on immediate rewards than on rewards received far in the future.

You can think of it in terms of money, would rather have money right now, or have it later.

Instead of using the raw cumulative reward, we use a discounted return:

\[Q^{\pi,\gamma}(s, a) \leftarrow r_0 + \gamma r_1 + \gamma^2 r_2 + \cdots | s_0 = s, a_0 = a\]

Where:

  • $\gamma \in [0,1]$ is the discount factor
  • $\gamma = 0$: Only immediate rewards matter
  • $\gamma = 1$: All future rewards are equally important
  • $\gamma \approx 0.99$: Common choice that slightly prioritizes near-term rewards

The corresponding objective function becomes:

\[\nabla_\theta J(\theta) \approx \frac{1}{N} \sum_{i=1}^{N} \sum_{t=1}^{T} \nabla_\theta \log \pi_\theta(a_{i,t}|s_{i,t}) \left(\sum_{t'=t}^{T} \gamma^{t'-t} r(s_{i,t'}, a_{i,t'})\right)\]

Why Discounting Helps:

  • Reduces variance: Distant rewards have less influence, so random events far in the future don’t dominate the gradient
  • Focuses learning: The agent learns to optimize for more predictable, near-term outcomes
  • Mathematical stability: Prevents infinite returns in continuing tasks

All of this comprises the complete Vanila Policy Gradient Algorithm which serves as the foundation for more advanced methods like PPO, TRPO, and GRPO, which we’ll explore in subsequent sections.

TRPO

The Sample Efficiency Problem

Our vanilla policy gradient algorithm works, but it has a critical flaw that makes it impractical for real-world applications. Let’s examine what happens during training:

  1. Collect trajectories using current policy π_θ
  2. Compute gradients from these trajectories
  3. Update policy θ → θ_new
  4. Throw away all previous data and start over

This last step is the problem. Imagine training a robot to walk - every time you make a small adjustment to the policy, you must collect entirely new walking data and discard everything you learned before. For complex tasks requiring thousands of timesteps per trajectory, this becomes computationally prohibitive.

Recall our policy gradient formula:

\[\nabla_\theta J(\theta) = \mathbb{E}_{\tau \sim \pi_\theta}\left[\sum_{t=1}^{T} \nabla_\theta \log \pi_\theta(a_t|s_t) \cdot A(s_t, a_t)\right]\]

The expectation $\mathbb{E}_{\tau \sim \pi \theta}$ means we must sample trajectories using the current policy π_θ. When we update θ, this distribution changes, invalidating all our previous samples.

Importance Sampling

What if we could reuse old data to estimate the performance of our new policy? This is exactly what importance sampling enables. The core idea is beautifully simple:

If you want to compute an expectation under distribution p, but you have samples from distribution q, you can reweight the samples by the ratio p/q.

For any function f(x), the expectation under distribution p can be computed as:

\[\mathbb{E}_{x \sim p}[f(x)] = \sum_x p(x)f(x)\]

But using importance sampling, we can compute this same expectation using samples from a different distribution q:

\[\mathbb{E}_{x \sim p}[f(x)] = \sum_x p(x)f(x) = \sum_x \frac{p(x)}{q(x)} \cdot q(x)f(x) = \mathbb{E}_{x \sim q}\left[\frac{p(x)}{q(x)} f(x)\right]\]

The magic happens in that middle step - we multiply and divide by q(x), creating a ratio p(x)/q(x) that reweights our samples.

Let’s see this in action with an example. Suppose we want to compute the expected value of f(x) = x under two different distributions:

Distribution p: P(x=1) = 0.5, P(x=3) = 0.5
Distribution q: P(x=1) = 0.8, P(x=3) = 0.2

Direct calculation under p: \(\mathbb{E}_{x \sim p}[f(x)] = 0.5 \times 1 + 0.5 \times 3 = 2.0\)

Using importance sampling with samples from q:

If we sample from q and get samples [1, 1, 1, 3], we can estimate the expectation under p by reweighting:

For x=1: weight = p(1)/q(1) = 0.5/0.8 = 0.625
For x=3: weight = p(3)/q(3) = 0.5/0.2 = 2.5

\[\mathbb{E}_{x \sim p}[f(x)] \approx \frac{1}{4}[0.625 \times 1 + 0.625 \times 1 + 0.625 \times 1 + 2.5 \times 3] = 2.0\]

The reweighted result matches our direct calculation!

Now we can revolutionize our policy gradient approach. Instead of:

\[\mathbb{E}_{\tau \sim \pi_\theta}[f(\tau)]\]

We can use:

\[\mathbb{E}_{\tau \sim \pi_{\theta_{old}}}\left[\frac{\pi_\theta(\tau)}{\pi_{\theta_{old}}(\tau)} f(\tau)\right]\]

Remember that trajectory probabilities factor as: \(\pi_\theta(\tau) = {p(s_1) \prod_{t=1}^{T} \pi_\theta(a_t|s_t)p(s_{t+1}|s_t, a_t)}\)

The environment dynamics $p(s_{t+1}|s_t, a_t)$ abd $p(s_1)$ are the same for both policies, so they cancel out in the ratio:

\[\frac{\pi_\theta(\tau)}{\pi_{\theta_{old}}(\tau)} = \frac{\prod_{t=1}^{T} \pi_\theta(a_t\|s_t)}{\prod_{t=1}^{T} \pi_{\theta_{old}}(a_t\|s_t)} = \prod_{t=1}^{T} \frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}\]

Our objective becomes:

\[J(\theta) = \mathbb{E}_{\tau \sim \pi_{\theta_{old}}}\left[\prod_{t=1}^{T} \frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)} \cdot R(\tau)\right]\]

This is huge! We can now:

  • Collect data with policy ${\pi_{\theta_{old}}}$
  • Reuse this data multiple times to evaluate different policies ${\pi_{\theta}}$
  • Dramatically improve sample efficiency

But there’s a catch. Importance sampling works well only when the two distributions are similar. If πθ becomes very different from πθ_old, the probability ratios can explode or vanish:

  • Ratio » 1: New policy assigns much higher probability to some actions
  • Ratio « 1: New policy assigns much lower probability to some actions
  • Ratio ≈ 0: Catastrophic - new policy never takes actions the old policy preferred

Consider what happens if one action has ratio = 100 while others have ratio = 0.01. A single high-ratio sample can dominate the entire gradient estimate, leading to:

  • Unstable training: Gradients vary wildly between batches
  • Poor convergence: The algorithm makes erratic updates
  • Sample inefficiency: We need many more samples to get reliable estimates

Constrained Policy Updates

The breakthrough insight: constrain how much the policy can change to keep importance sampling ratios well-behaved. This leads us naturally to the concept of trust regions - regions where we trust our importance sampling approximation to be accurate.

But, we must also ask. How do we guarantee that our policy updates always improve performance?

These observations bring us to two key concepts:

  • The Minorize-Maximization (MM) algorithm
  • Trust regions

Minorize-Maximization (MM) Algorithm

Can we guarantee that any policy update always improves the expected rewards? This seems impossible, but it’s theoretically achievable through the MM algorithm.

The idea: Instead of directly optimizing the complex true objective η(θ), we iteratively optimize simpler lower bound functions M(θ) that approximate η(θ) locally.

The MM algorithm follows this iterative process:

  1. Find a lower bound M that approximates the expected reward η locally at the current guess θ_i
  2. Optimize the lower bound M to find the next policy guess θ_{i+1}
  3. Repeat until convergence

For this to work, M must be:

  • A lower bound: M(θ) ≤ η(θ) for all θ
  • Tight at current point: M(θ_i) = η(θ_i)
  • Easier to optimize: M should be simpler than η (typically quadratic)

The lower bound function has the form: $M(\theta) = g \cdot (\theta - \theta_{old}) - \frac{1}{2}(\theta - \theta_{old})^T F (\theta - \theta_{old})$

This is a quadratic approximation where:

  • g is the gradient at θ_old
  • F is a positive definite matrix (often related to the Hessian)

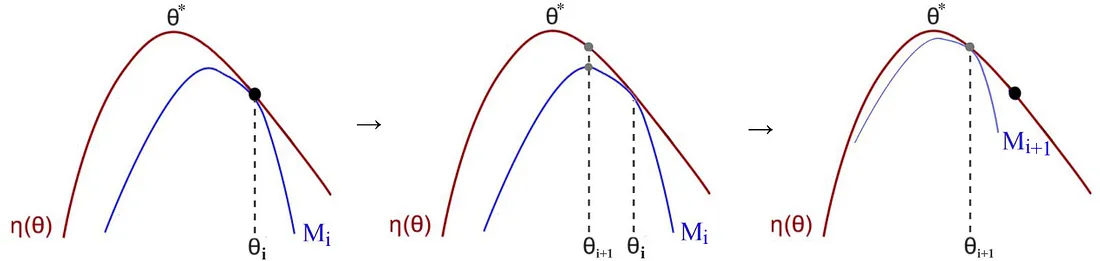Image of Minorize Maximization algorithm Image taken from RL — Trust Region Policy Optimization (TRPO) Explained

If M is a lower bound that never crosses η, then maximizing M must improve η.

Proof sketch:

  • Since $M(\theta_{\text{old}}) = \eta(\theta_{\text{old}})$ and $M(\theta) \leq \eta(\theta)$ everywhere
  • If we find $\theta_{\text{new}}$ such that $M(\theta_{\text{new}}) > M(\theta_{\text{old}})$
  • Then $\eta(\theta_{\text{new}}) \geq M(\theta_{\text{new}}) > M(\theta_{\text{old}}) = \eta(\theta_{\text{old}})$
  • Therefore $\eta(\theta_{\text{new}}) > \eta(\theta_{\text{old}})$ ✓

In simpler terms, we have a function $\eta(\theta)$ parameterized by $\theta$ (the weights of our neural network). It is not computationally tractable to optimize this function directly. Hence we create a close approximation function $M(\theta)$ using the lower bound function form described above. This approximation comes from the general theory of Minorize-Maximization algorithms (see Hunter & Lange, 2004).

This approximation $M(\theta)$ is computationally feasible and easier to optimize. What we have proved here is that as we improve $M(\theta)$, that improvement guarantees we also improve $\eta(\theta)$.

By optimizing a lower bound function approximating η locally, MM guarantees policy improvement every iteration and leads us to the optimal policy eventually.

Trust Regions

There are two major optimization paradigms:

  1. Line Search (like gradient descent): Choose direction first, then step size
  2. Trust Region: Choose maximum step size first (the size of the trust region), then find optimal point within that region

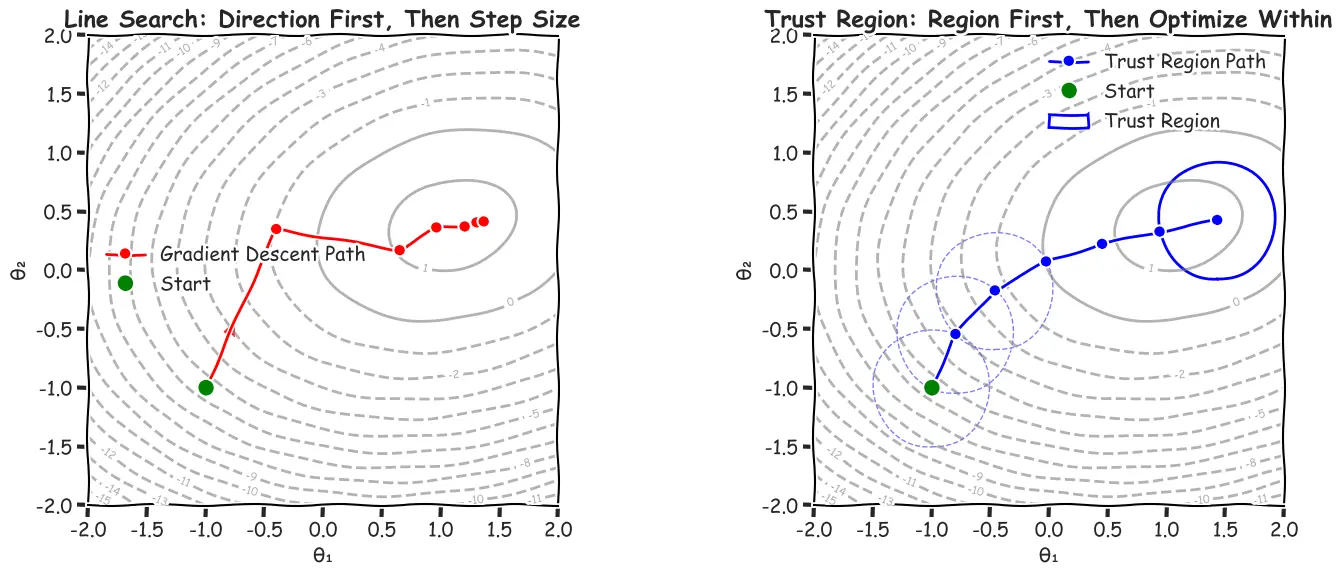
Image of Line search vs Trust Region

In trust region methods, we:

  1. Define a trust region of radius δ around current policy θ_old
  2. Find the optimal policy within this constrained region
  3. Adapt the radius based on how well our approximation worked

The optimization problem becomes: $\max_{\theta} \; M(\theta)$ $\text{subject to} \; |\theta - \theta_{old}| \leq \delta$

Adaptive Trust Region Sizing

The trust region radius δ can be dynamically adjusted:

  • If approximation is good: Expand δ for next iteration
  • If approximation is poor: Shrink δ for next iteration
  • If policy diverges too much: Shrink δ to prevent importance sampling breakdown

Why Trust Regions Work for RL

In reinforcement learning, trust regions serve a dual purpose:

  1. Mathematical: Keep our quadratic approximation M valid
  2. Statistical: Prevent importance sampling ratios from exploding

When policies change too much, both our lower bound approximation AND our importance sampling become unreliable. Trust regions keep us in the safe zone for both.

Mathematical Notation Reference
Symbol Meaning
$\pi_\theta(a|s)$ Policy probability of action a given state s
$\pi_{\theta_{old}}(a|s)$ Old policy probability
$\tau$ Trajectory $(s_1, a_1, s_2, a_2, \ldots)$
$\pi_\theta(\tau)$ Probability of trajectory under policy $\pi_\theta$
$\frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}$ Importance sampling ratio for single timestep
$\prod_{t=1}^{T} \frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}$ Importance sampling ratio for full trajectory
$R(\tau)$ Total reward of trajectory
$A(s_t, a_t)$ Advantage function
$\eta(\theta)$ Expected reward under policy $\pi_\theta$
$M(\theta)$ Lower bound function in MM algorithm
$\theta_{old}$ Current policy parameters
$\delta$ Trust region radius
$F$ Positive definite matrix (approximating curvature)
$g$ Policy gradient vector


Trust Region Policy Optimization (TRPO)

Now we can finally understand how TRPO elegantly combines all the concepts we’ve explored:

  1. Importance Sampling - to reuse old data efficiently
  2. MM Algorithm - to guarantee policy improvement
  3. Trust Regions - to constrain policy changes and keep approximations valid

TRPO is a culmination of these ideas into a practical, theoretically-grounded algorithm.

Recall that our original objective was:

\[J(\pi) = \mathbb{E}_{\tau \sim \pi}[R(\tau)]\]

This is the expected return (total reward) when following policy π. Instead of maximizing absolute performance $J(\pi’)$, TRPO maximizes the policy improvement:

\[\max_{\pi'} J(\pi') - J(\pi)\]

This is mathematically equivalent to maximizing $J(\pi’)$ (since $J(\pi)$ is constant), but conceptually important - we’re explicitly measuring progress from our current policy.

Why focus on improvement? Because we can construct better approximations for the improvement $J(\pi’) - J(\pi)$ than for the absolute performance $J(\pi’)$. The MM algorithm works by finding lower bounds for this improvement.

To apply the MM algorithm, TRPO constructs a lower bound function ℒ that uses importance sampling:

\[\mathcal{L}_\pi(\pi') = \frac{1}{1-\gamma} \mathbb{E}_{s\sim d^\pi} \left[ \frac{\pi'(a|s)}{\pi(a|s)} A^\pi(s,a) \right] = \mathbb{E}_{\tau \sim \pi} \left[ \sum_{t=0}^{\infty} \gamma^t \frac{\pi'(a_t|s_t)}{\pi(a_t|s_t)} A^\pi(s_t, a_t) \right]\]

ℒ looks complex, but let’s break this down piece by piece to understand what’s really happening here.

The discounted state visitation distribution $d^\pi(s)$ tells us how often we expect to visit each state when following policy π:

\[d^\pi(s) = (1-\gamma) \sum_{t=0}^{\infty} \gamma^t P(s_t = s|\pi)\]

Think of this as a “popularity contest” for states. If γ = 1, this becomes just the regular state visit frequency under policy π. But when γ < 1, we care more about states we visit early in episodes than those we reach later. It’s like asking: “If I run my policy many times, which states will I spend most of my time in, giving more weight to earlier visits?”

The advantage function $A^\pi(s,a)$ we’ve already met - it tells us how much better taking action $a$ in state $s$ is compared to what the policy would do on average in that state.

But here’s where the magic happens. The function ℒ is essentially asking a clever question using importance sampling: “If I reweight all the actions my current policy π took according to how likely my new policy π’ would be to take them, what would my expected advantage be?”

This is brilliant because it lets us estimate how well policy π’ would perform without actually running it in the environment. We just take all our old experience from policy π and reweight it according to the probability ratio $\frac{\pi’(a|s)}{\pi(a|s)}$. When the new policy is more likely to take an action than the old one, we give that experience more weight. When it’s less likely, we give it less weight.

This importance sampling approach is what allows TRPO to reuse old data efficiently - a huge computational win over vanilla policy gradients that throw away all previous experience after each update.

The theoretical foundation comes from this crucial bound (proven in Appendix 2 of the TRPO paper):

\[J(\pi') - J(\pi) \geq \mathcal{L}_\pi(\pi') - C\sqrt{\mathbb{E}_{s\sim d^\pi}[D_{KL}(\pi' \| \pi)[s]]}\]

This tells us:

  • Left side: True policy improvement
  • Right side: Our lower bound estimate minus a penalty term

The penalty term grows with KL divergence, so the bound becomes loose when policies differ too much.

Consider reading this blog to get a better idea about KLD

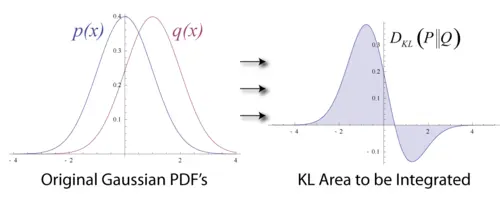Image of KLD Image taken from Wikipedia

The KL divergence measures how different two probability distributions are:

\[D_{KL}(P \| Q) = \sum_x P(x) \log \frac{P(x)}{Q(x)}\]

For continuous distributions, this becomes:

\[D_{KL}(P \| Q) = \int P(x) \log \frac{P(x)}{Q(x)} dx\]

Think of KL divergence as asking: “If I have samples from distribution P, how surprised would I be if I thought they came from distribution Q instead?” When the distributions are identical, KL divergence is zero. As they become more different, the divergence grows.

TRPO can be formulated in two mathematically equivalent ways:

KL-Penalized (Unconstrained): \(\max_{\pi'} \mathcal{L}_\pi(\pi') - C\sqrt{\mathbb{E}_{s\sim d^\pi}[D_{KL}(\pi' \| \pi)[s]]}\)

KL-Constrained: \(\max_{\pi'} \mathcal{L}_\pi(\pi')\) \(\text{subject to } \mathbb{E}_{s\sim d^\pi}[D_{KL}(\pi'||\pi)[s]] \leq \delta\)

These formulations arise directly from the theoretical bound we mentioned earlier:

\[J(\pi') - J(\pi) \geq \mathcal{L}_\pi(\pi') - C\sqrt{\mathbb{E}_{s\sim d^\pi}[D_{KL}(\pi'||\pi)[s]]}\]

The unconstrained version simply maximizes this lower bound directly. The constrained version takes a different approach: instead of penalizing large KL divergences, it prevents them entirely by adding a hard constraint.

These are mathematically equivalent due to Lagrangian duality - a beautiful result from optimization theory. For every penalty coefficient C in the unconstrained problem, there exists a constraint threshold δ in the constrained problem that gives the same optimal solution. You can think of it like this: instead of saying “I’ll pay a penalty for going over the speed limit,” you’re saying “I absolutely won’t go over the speed limit.” Both approaches can lead to the same driving behavior, just with different enforcement mechanisms.

The lower bound is what we try to maximize to find the optimum $\theta$

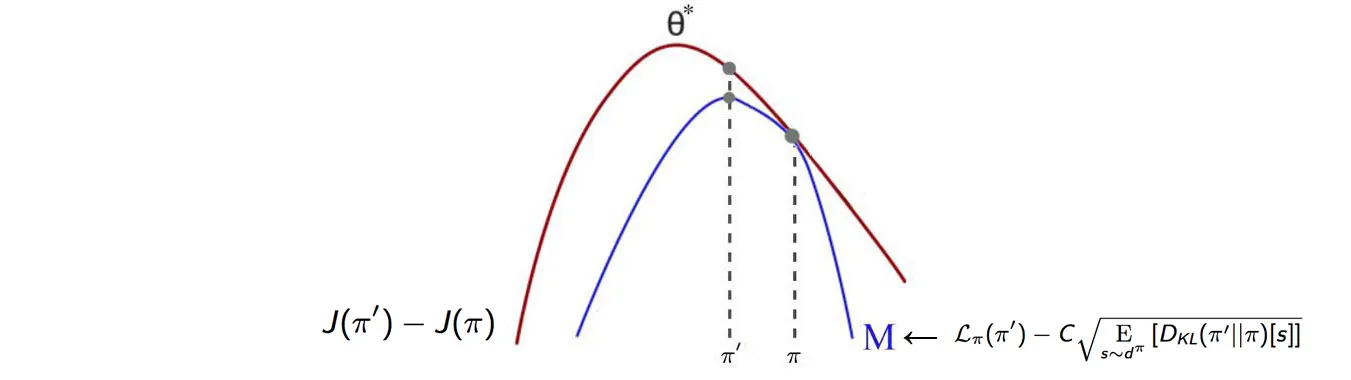Image of lower bound of constrained problem Image taken from here

However, in practice, the constrained formulation wins by a landslide. Here’s why: the penalty coefficient C becomes a nightmare to tune when the discount factor γ gets close to 1. As γ approaches 1, the coefficient explodes, making the algorithm incredibly sensitive to small changes in γ. Imagine trying to tune a parameter that changes by orders of magnitude when you adjust γ from 0.99 to 0.995 - it’s practically impossible.

\[C \propto 1/(1-\gamma)^2\]

The constrained version, on the other hand, gives you direct, interpretable control. The parameter δ simply says “don’t let the policy change too much,” which is much easier to understand and tune across different environments. It’s the difference between having a thermostat that directly controls temperature versus one that requires you to calculate complex equations involving heat transfer coefficients.

This practical insight would later inspire PPO’s breakthrough innovation. PPO took the unconstrained formulation and made it work brilliantly by replacing the complex second-order penalty with a simple first-order clipping mechanism. Instead of computing expensive Fisher Information Matrices, PPO just clips the importance sampling ratios directly - achieving similar performance with a fraction of the computational cost.

The beauty of TRPO lies in its theoretical guarantee. Since we have the fundamental bound:

\[J(\pi') - J(\pi) \geq \mathcal{L}_\pi(\pi') - C\sqrt{\mathbb{E}_{s\sim d^\pi}[D_{KL}(\pi'(·|s) \| \pi(·|s))]}\]

TRPO’s algorithm ensures three key things happen:

  1. Optimize $\mathcal{L}_\pi(\pi’)$ using importance sampling
  2. Constrain the KL divergence to stay small
  3. Rely on the fact that $\mathcal{L}_\pi(\pi) = 0$ when $\pi’ = \pi$

This last point is crucial and deserves explanation.

Why is ℒ_π(π) = 0? At the current policy, the importance sampling ratio becomes $\frac{\pi(a|s)}{\pi(a|s)} = 1$ for all actions. So we get:

\[\mathcal{L}_\pi(\pi) = \mathbb{E}_{s\sim d^\pi} \left[ \mathbb{E}_{a \sim \pi} \left[ 1 \cdot A^\pi(s,a) \right] \right] = \mathbb{E}_{s\sim d^\pi} \left[ \mathbb{E}_{a \sim \pi} \left[ A^\pi(s,a) \right] \right]\]

But by definition, the advantage function has zero expectation under the policy - $\mathbb{E}_{a \sim \pi}[A^\pi(s,a)] = 0$ because it measures how much better each action is compared to the average. This means if we can make ℒ_π(π’) > 0 while keeping KL divergence small, we’re guaranteed that J(π’) > J(π). TRPO never moves backwards.

You can read more about the proof here

$\mathcal{L}_\pi(\pi’) \geq 0$ implies $J(\pi’) \geq J(\pi)$ (Our new policy will always be better or equal to our current policy)

TRPO’s guarantee: Every policy update improves performance or leaves it unchanged. We never move backwards.

Think of TRPO this way:

  1. Sample trajectories with current policy $\pi$
  2. Estimate how well any nearby policy $\pi’$ would do on these same trajectories (importance sampling)
  3. Find the best nearby policy within our trust region (constrained optimization)
  4. Verify the policy is actually better before committing (safety check)

The trust region ensures our importance sampling estimates remain accurate, while the MM algorithm structure guarantees we always improve. The constrained optimization problem: \(\max_{\pi'} \mathcal{L}_\pi(\pi')\) \(\text{subject to } \mathbb{E}_{s\sim d^\pi}[D_{KL}(\pi'||\pi)[s]] \leq \delta\)

looks intimidating, but we can solve it elegantly using a Taylor expansion around our current policy parameters θ_k. This is where the mathematical beauty of TRPO really shines through.

Image of Taylor Series expansion Definition from Wikipedia Let’s expand both the objective function and the constraint to second order around $\theta_k$. For the objective function $\mathcal{L}$:

\[\mathcal{L}_{\theta_k}(\theta) \approx \mathcal{L}_{\theta_k}(\theta_k) + g^T (\theta - \theta_k) + \frac{1}{2}(\theta - \theta_k)^T H_{\mathcal{L}} (\theta - \theta_k)\]

Where:

  • g = ∇θ Lθₖ(θ) |_θₖ (the gradient of the objective at θₖ)
  • HL = ∇²θ Lθₖ(θ) |θₖ (the Hessian of the objective at θₖ)
We can skip the terms beyond second order because they become negligibly small when $\theta$ is close to $\theta_k$. This is the fundamental assumption of trust region methods - we’re making small enough steps that higher-order terms don’t significantly affect our approximation quality.

For the KL constraint: \(\overline{D}_{KL}(\theta|\theta_k) \approx \overline{D}_{KL}(\theta_k|\theta_k) + \nabla_\theta \overline{D}_{KL}(\theta|\theta_k)|_{\theta_k}^T (\theta - \theta_k) + \frac{1}{2}(\theta - \theta_k)^T H_{KL} (\theta - \theta_k)\)

Now comes the key insight that simplifies everything. At the current policy θ_k, several terms vanish:

  • $\mathcal{L}_{\theta_k}(\theta_k) = 0$ (we showed this earlier - the advantage has zero expectation)
  • $\overline{D}_{KL}(\theta_k|\theta_k) = 0$ (KL divergence of a distribution with itself is always zero)
  • ∇*θ D̄_KL(θ   θₖ) *θₖ = 0 (the gradient of KL divergence at the reference point is zero)

This leaves us with a beautifully clean quadratic optimization problem:

\(\max_\theta g^T (\theta - \theta_k)\) \(\text{subject to } \frac{1}{2}(\theta - \theta_k)^T H_{KL} (\theta - \theta_k) \leq \delta\)

where g is the policy gradient: \(g = \nabla_\theta \mathcal{L}_{\theta_k}(\theta) |_{\theta_k}\)

and $H_{KL}$ is the Hessian of the KL divergence, which has a special name: the Fisher Information Matrix (FIM):

\[H_{KL} = \nabla^2_\theta \overline{D}_{KL}(\theta|\theta_k) |_{\theta_k} = F = \mathbb{E}_{s,a \sim \pi_k} \left[ \nabla_\theta \log \pi_\theta(a|s) \nabla_\theta \log \pi_\theta(a|s)^T \right]\]

This constrained quadratic optimization problem has a closed-form solution that can be derived using Lagrange multipliers. Setting up the Lagrangian:

\[\mathcal{L}(\theta, \lambda) = g^T (\theta - \theta_k) - \lambda \left( \frac{1}{2}(\theta - \theta_k)^T F (\theta - \theta_k) - \delta \right)\]

Taking the gradient with respect to θ and setting it to zero: \(\nabla_\theta \mathcal{L} = g - \lambda F (\theta - \theta_k) = 0\)

Solving for the optimal step: \(\theta - \theta_k = \frac{1}{\lambda} F^{-1} g\)

To find λ, we substitute back into the constraint: \(\frac{1}{2} \left( \frac{1}{\lambda} F^{-1} g \right)^T F \left( \frac{1}{\lambda} F^{-1} g \right) = \delta\)

\[\frac{1}{2\lambda^2} g^T F^{-1} g = \delta\] \[\lambda = \sqrt{\frac{g^T F^{-1} g}{2\delta}}\]

Putting it all together, we get the Natural Policy Gradient update:

\[\theta_{k+1} = \theta_k + \sqrt{\frac{2\delta}{g^T F^{-1} g}} F^{-1} g\]

Why “Natural”? This is where things get philosophically beautiful. Regular gradient descent uses the Euclidean distance in parameter space - it treats all parameter changes as equal. But this is fundamentally wrong for probability distributions!

Consider two neural networks that represent the same policy but with different parameterizations. Vanilla gradient descent would give them different updates, even though they’re the same policy. The Natural Policy Gradient fixes this by using the Fisher Information Matrix to measure distance in the space of probability distributions rather than parameter space.

The Fisher Information Matrix captures the “curvature” of the log-likelihood surface. Areas where small parameter changes cause big changes in the policy get more weight in the distance metric. This makes the algorithm reparameterization invariant - the actual policy updates remain the same regardless of how you parameterize your neural network.

Think of it like this: if you’re navigating on a curved surface, you shouldn’t use straight-line distances to plan your path. The Fisher Information Matrix gives you the “natural” metric for that curved space, ensuring you take the most efficient steps toward better policies.

Image of Euclidean gradient descent vs natural gradient descent

The Backtracking Line Search

Our elegant mathematical derivation gives us the Natural Policy Gradient update:

\[\theta_{k+1} = \theta_k + \sqrt{\frac{2\delta}{g^T F^{-1} g}} F^{-1} g\]

But here’s the rub: this assumes our quadratic approximation is perfect. In reality, neural networks are highly nonlinear, and our Taylor expansion is only valid in a small neighborhood around $\theta_k$. The computed step might violate our KL constraint or even decrease performance when the approximation breaks down.

TRPO’s solution is beautifully practical: backtracking line search. Instead of blindly taking the full computed step, TRPO modifies the update to:

\[\theta_{k+1} = \theta_k + \alpha^j \sqrt{\frac{2\delta}{g^T F^{-1} g}} F^{-1} g\]

where $\alpha \in (0, 1)$ is the backtracking coefficient (typically 0.5), and $j$ is the smallest nonnegative integer such that the new policy satisfies both:

  1. The KL constraint: 𝔼{s∼d^π}[D_KL(π{θ{k+1}}(·|s) ‖ π{θₖ}(·|s))] ≤ δ
  2. Positive improvement: ℒ{θₖ}(θ{k+1}) ≥ 0

This conservative verification ensures TRPO never violates its theoretical guarantees, even when the quadratic approximation becomes inaccurate. It’s the algorithm’s safety net - systematically reducing the step size until both conditions are met.

However, there’s a computational nightmare lurking here. The Natural Policy Gradient requires computing $F^{-1}g$, which means inverting the Fisher Information Matrix:

\[F = \mathbb{E}_{s,a \sim \pi_k} \left[ \nabla_\theta \log \pi_\theta(a|s) \nabla_\theta \log \pi_\theta(a|s)^T \right]\]

For modern deep networks with millions of parameters, F is a massive n×n matrix. Computing its inverse is O(n³) - completely impractical. Even storing the full matrix requires O(n²) memory, which quickly becomes impossible for large networks.

This computational bottleneck is what led to the development of Truncated Natural Policy Gradient, and ultimately to TRPO’s clever use of conjugate gradient methods to approximate the matrix inversion without ever computing F⁻¹ explicitly.

Truncated Natural Policy Gradient

The solution to our computational nightmare is elegantly simple: instead of computing F⁻¹g directly, we use the Conjugate Gradient method to solve the linear system:

\[F x = g\]

This iterative approach finds x ≈ F⁻¹g without ever computing the matrix inverse, requiring only matrix-vector products Fv. It’s like finding the solution to a puzzle without having to understand every piece - we just need to know how the pieces interact.

Conjugate Gradient works by generating search directions that are “conjugate” - meaning they’re orthogonal after being transformed by matrix F. This ensures that each new search direction doesn’t undo progress from previous iterations. For quadratic problems like ours, CG guarantees finding the exact solution in at most n steps (where n is the number of parameters), but typically converges much faster in practice.

Image of Taylor Series expansion

The key insight is that we never need to compute or store the full Fisher Information Matrix. Instead, we only need the matrix-vector product $Fx$ for any vector $x$. This can be computed efficiently using automatic differentiation:

\[Fx = \nabla_\theta \left( \left( \nabla_\theta \overline{D}_{KL}(\theta||\theta_k) \right)^T x \right)\]

This Hessian-vector product gives us exactly what conjugate gradient needs without ever materializing the massive $F$ matrix.

The Complete TRPO Algorithm

TRPO weaves together all these concepts into a surprisingly elegant algorithm that carefully balances theoretical guarantees with practical implementation:

Step 1: Data Collection

  • Collect trajectories using the current policy $\pi_k$
  • Estimate the advantage function $A^{\pi_k}$ using any method (GAE, Monte Carlo returns, or temporal difference learning)

Step 2: Gradient Computation

  • Compute the policy gradient \(g = \nabla_\theta \mathcal{L}_{\theta_k}(\theta) \|_{\theta_k}\)
  • Set up the Fisher Information Matrix function for conjugate gradient operations

Step 3: Search Direction

  • Solve $Fx = g$ using Conjugate Gradient to get the search direction $x$
  • This gives us the natural gradient direction without explicitly inverting $F$

Step 4: Step Size Calculation

  • Compute the initial step size to satisfy the trust region constraint
  • Calculate $\alpha = \sqrt{\frac{2\delta}{g^T F^{-1} g}}$

Step 5: Conservative Verification (Line Search with Exponential Backoff)

  • Propose an update: $\theta’ = \theta_k + \alpha \cdot x$
  • Verify two critical conditions:
  • KL divergence constraint: \(\mathbb{E}_{s\sim d^\pi}[D_{KL}(\pi'(·\|s) \| \pi(·\|s))] \leq \delta\)
  • Surrogate improvement: $\mathcal{L}_{\theta_k}(\theta’) \geq 0$
  • If either verification fails: reduce $\alpha$ (typically by half) and try again
  • Only commit to the policy update after both conditions are satisfied

This conservative approach guarantees the theoretical properties we derived, but it also reveals TRPO’s fundamental tension between theory and practice. The algorithm is theoretically beautiful but computationally demanding, requiring multiple verification steps and potential backtracking that can make each update quite expensive.

TRPO’s Limitations

Despite its theoretical elegance, TRPO faces several practical challenges that motivated simpler alternatives:

  • Computational Overhead: Computing Fisher Information Matrices and running conjugate gradient makes each update significantly more expensive than first-order methods like Adam
  • Sample Inefficiency: Requires large batch sizes to accurately estimate the FIM - small batches lead to noisy estimates and unstable training
  • Scalability Issues: Second-order computations become impractical for very large neural networks where first-order methods excel

TRPO’s story represents a classic tension in machine learning: the trade-off between theoretical rigor and practical utility. While TRPO provided crucial theoretical insights about policy optimization - principled policy updates, trust region concepts, and guaranteed improvement - its computational complexity limited its real-world impact.

This limitation sparked a natural question: could we achieve similar performance guarantees with a much simpler algorithm? The answer would come in the form of Proximal Policy Optimization (PPO), which took TRPO’s core insights and packaged them into an algorithm so simple and effective that it would become the workhorse of modern policy optimization.

As we noted earlier from the PPO paper: “Q-learning (with function approximation) fails on many simple problems and is poorly understood, vanilla policy gradient methods have poor data efficiency and robustness; and trust region policy optimization (TRPO) is relatively complicated, and is not compatible with architectures that include noise (such as dropout) or parameter sharing.”

PPO’s breakthrough was recognizing that you don’t need complex second-order methods to implement trust regions effectively. Instead of computing Fisher Information Matrices and running conjugate gradient, PPO simply clips the importance sampling ratios directly. This first-order approach achieves similar practical performance while being orders of magnitude simpler to implement and debug.

Note: TRPO in a crux is simple, it is a constrained optimization problem. To solve which we need second order derivatives. Which is computationally expensive and no current ML framework solves it without significant overhead. But do know, it is a tough topic to truly understand. One needs to be well-versed with many prerequisite mathematical knowledge. Do not be dishearted if it takes you time to understand it thorougly. Read slowly, daily, iteratively.

Proximal Policy Optimization (PPO)

PPO emerged from a simple observation: what if we could achieve TRPO’s stability guarantees without all the computational complexity? The genius of PPO lies in replacing TRPO’s hard KL constraint with a clever objective function that naturally prevents large policy updates.

Let’s first understand the core innovation. Remember TRPO’s constrained optimization problem:

\[\max_{\theta} \mathcal{L}_{\theta_{old}}(\theta) \quad \text{subject to } \mathbb{E}_{s \sim d^{\pi_{old}}}[D_{KL}(\pi_{old}(\cdot|s) || \pi_\theta(\cdot|s))] \leq \delta\]

PPO asks: instead of explicitly constraining the KL divergence, what if we modify the objective function itself to penalize large policy changes? This transforms a constrained optimization problem into an unconstrained one that standard optimizers like Adam can handle.

The Clipped Surrogate Objective

PPO introduces a brilliantly simple idea. Define the probability ratio:

\[r_t(\theta) = \frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}\]

This ratio tells us how much more (or less) likely the new policy is to take the same action compared to the old policy. When $r_t(\theta) = 1$, the policies agree perfectly. When $r_t(\theta) = 2$, the new policy is twice as likely to take that action.

The vanilla policy gradient objective using importance sampling would be:

\[L^{IS}(\theta) = \mathbb{E}_t[r_t(\theta) \cdot A_t]\]

But this can lead to destructively large policy updates when $r_t(\theta)$ becomes very large or very small. PPO’s innovation is to clip this ratio:

\[L^{CLIP}(\theta) = \mathbb{E}_t[\min(r_t(\theta) \cdot A_t, \text{clip}(r_t(\theta), 1-\epsilon, 1+\epsilon) \cdot A_t)]\]

Image of Taylor Series expansion Image taken from paper

Let’s unpack this equation with concrete examples to build intuition.

Case 1: Positive Advantage (A_t > 0)

When an action led to better-than-expected rewards, we want to increase its probability. Let’s say $A_t = 2$ and $\epsilon = 0.2$.

  • If $r_t(\theta) = 0.5$ (new policy half as likely):

    • Unclipped objective: $0.5 \times 2 = 1$
    • Clipped objective: $\min(1, 0.8 \times 2) = 1$
    • No clipping occurs since we’re making the policy worse for a good action

  • If $r_t(\theta) = 1.5$ (new policy 50% more likely):

    • Unclipped objective: $1.5 \times 2 = 3$
    • Clipped objective: $\min(3, 1.2 \times 2) = 2.4$
    • Clipping kicks in! We cap the improvement to prevent overconfidence

The key insight: for positive advantages, clipping prevents us from changing the policy too aggressively in the “good” direction. Once $r_t(\theta) > 1 + \epsilon$, there’s no benefit to increasing it further.

Case 2: Negative Advantage (A_t < 0)

When an action led to worse-than-expected rewards, we want to decrease its probability. Let’s say $A_t = -2$ and $\epsilon = 0.2$.

  • If $r_t(\theta) = 0.5$ (new policy half as likely):

    • Unclipped objective: $0.5 \times (-2) = -1$
    • Clipped objective: $\min(-1, 0.8 \times (-2)) = -1.6$
    • Clipping makes the objective more negative, encouraging further reduction

  • If $r_t(\theta) = 1.5$ (new policy 50% more likely):

    • Unclipped objective: $1.5 \times (-2) = -3$
    • Clipped objective: $\min(-3, 1.2 \times (-2)) = -3$
    • No clipping since we’re increasing probability of a bad action

For negative advantages, clipping prevents us from reducing the probability too aggressively. Once $r_t(\theta) < 1 - \epsilon$, there’s no benefit to decreasing it further.

The Mathematical Beauty of PPO’s Objective

The clipped objective creates a “trust region” implicitly. When the policy changes too much (beyond $1 \pm \epsilon$), the gradient of the clipped objective becomes zero with respect to $\theta$. This elegant mechanism automatically prevents destructive updates without requiring second-order optimization.

To see this mathematically, consider the gradient when $A_t > 0$ and $r_t(\theta) > 1 + \epsilon$:

\[\frac{\partial L^{CLIP}}{\partial \theta} = \frac{\partial}{\partial \theta}[\text{clip}(r_t(\theta), 1-\epsilon, 1+\epsilon) \cdot A_t] = 0\]

The gradient vanishes because the clipped value $(1+\epsilon)$ doesn’t depend on $\theta$. This creates a “flat” region in the loss landscape that prevents further movement in that direction.

PPO with Adaptive KL Penalty

Before arriving at the clipped objective, the PPO paper explored a KL penalty approach that directly connects to TRPO:

\[L^{KLPEN}(\theta) = \mathbb{E}_t[r_t(\theta) \cdot A_t - \beta \cdot D_{KL}(\pi_{\theta_{old}}(\cdot|s_t) || \pi_\theta(\cdot|s_t))]\]

This is exactly the unconstrained version of TRPO’s problem! The Lagrangian of TRPO’s constrained optimization:

\[\max_{\theta} \mathcal{L}_{\theta_{old}}(\theta) - \lambda(\mathbb{E}[D_{KL}] - \delta)\]

becomes PPO’s KL penalty objective when we fix $\beta = \lambda$. The key difference: PPO adapts $\beta$ dynamically during training:

if kl_divergence > 1.5 * target_kl:
    beta *= 2  # Increase penalty
elif kl_divergence < target_kl / 1.5:
    beta /= 2  # Decrease penalty

However, this adaptive mechanism proved finicky in practice. The clipped objective achieved similar goals with fixed hyperparameters, making it the preferred approach.

Why Multiple Epochs Work: The Importance Sampling Perspective

A subtle but crucial aspect of PPO is performing multiple epochs of updates on the same data. This seems to violate our earlier concern about importance sampling breaking down when policies diverge. The clipping mechanism is precisely what makes this safe.

Consider what happens over multiple epochs:

  1. Epoch 1: Policy changes slightly, ratios stay near 1
  2. Epoch 2: For trajectories where policy already changed, clipping prevents further movement
  3. Epochs 3-10: Most gradients are zero due to clipping, only “unexploited” trajectories contribute

The clipping essentially creates a curriculum where different parts of the data become “active” in different epochs, naturally preventing overfitting to any particular trajectory.

PPO’s clipping prevents the fine-tuned model from diverging too far from the base model’s distribution, maintaining fluency while optimizing for human preferences. This is why responses from RLHF models feel coherent - they’re constrained to stay within a trust region of the original model’s behavior.

The journey from policy gradients through TRPO to PPO represents a beautiful example of how complex theoretical insights can be distilled into simple, practical algorithms. PPO takes TRPO’s guarantee of monotonic improvement and approximates it with a first-order method that captures the essential insights: prevent destructive updates, enable data reuse, and maintain computational simplicity.

MoE

Image of MoE paper abstract

Link to paper: Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer
Link to implementation: [WORK IN PROGRESS]

Quick Summary

This 2017 paper by Shazeer et al. introduces a novel approach to dramatically increase neural network capacity without proportionally increasing computational costs. The core innovation is the Sparsely-Gated Mixture-of-Experts (MoE) layer, which contains thousands of feed-forward neural networks (experts), with a trainable gating network that selectively activates only a small subset of experts for each input example.

Key highlights:

  • The authors achieve over 1000x improvements in model capacity while maintaining computational efficiency
  • Their approach addresses several challenges of conditional computation, including GPU utilization and load balancing
  • When applied to Language Modeling and machine translation tasks, their MoE models significantly outperform state-of-the-art models with lower computational cost
  • Their largest model contains up to 137 billion parameters and demonstrates continued performance improvements with increased capacity

This paper represents a significant advancement in scaling neural networks efficiently, presaging some of the techniques that would later become important in very large language models.


Another explosive paper, in 2017. Talk about being a crazy year right. Well to be perfectly honest MOE was actually introduced in 1991 in the paper Adaptive Mixture of Local Experts. But Noam et al introduced the idea to LSTMs, which really blew up.

Problem

The capacity of a neural network to absorb information is limited by its number of parameters.

Solution

Conditional computation, where parts of the network are active on a per-example basis, has been proposed in theory as a way of dramatically increasing model capacity without a proportional increase in computation.

The following blogs helped me immensely while writing this section

Image of MoE intuition

A simple intuition behind MoE can be seen as above, A single dense neural network is like a big student. Who has general knowledge about a lot of things without being particularly great at any one topic. When you ask him a question he takes his time to think and answers you, He also eats a lot because he is big.

But with a MoE layer, a smart router reads the question and directs it to the right expert. That expert gives a focused answer since they only need to worry about their specialty. As we’re only activating one small expert instead of the entire large model, we use much less computation while still having access to lots of specialized knowledge.

The above visualization is good for intuition point of view, but that is not how MoEs actually work in practice. For starter each expert is not an expert in a topic but expert in tokens, some can be punctuation experts, some can be noun experts etc.(More on this later)

This work introduced MoEs to LSTMs, so let us proceed forward in understanding that. Consider reading the following blog Understanding LSTM Networks by Christopher Olah & Recurrent Neural Networks (RNNs), Clearly Explained!!! by Josh Starmer if you need a refresher on the topic.

Image of MoE for RNNs

In an MoE model, the Fully connected neural network(FCNN) (Or the hiddens state in case of RNNs & LSTMs) is replaces with an MoE layer. The MoE layer consists of a gating function which outputs a probability distribution of likely experts. The experts themselves are smaller FCNN. The output of the experts is multiplied with their probability after which it is finally summed over.

Image of MoE layer

The idea seems simple enough, but there are multiple complexities like:

  • How do you create a fair gating function?
  • How many experts do you choose?
  • How many tokens do you send to each expert?

Let’s us go through each question one by one.

Note: We will see many changes that were made on this idea as we progress, but this was the foundational paper on MoEs for large models. So it is crucial that you understand it well.

Sparse vs Dense Networks

Image of sparse and dense MoE

Dense Networks: Every parameter is used for every input

  • High computational cost that scales linearly with parameters
  • Limited by memory and compute constraints
  • Parameters must be “generalists” handling all types of inputs

Sparse Networks (MoE): Only a subset of parameters are used per input

  • Computational cost scales with active experts, not total experts
  • Can have 1000x more parameters with similar compute budget
  • Parameters can be highly specialized for specific patterns

conditional computation allows us to scale model capacity without proportional compute scaling. It’s like having a library with thousands of specialized books, but only reading the few relevant ones for each question.

The Gating Network

First let us understand how the output is calculated in a sparse MoE.

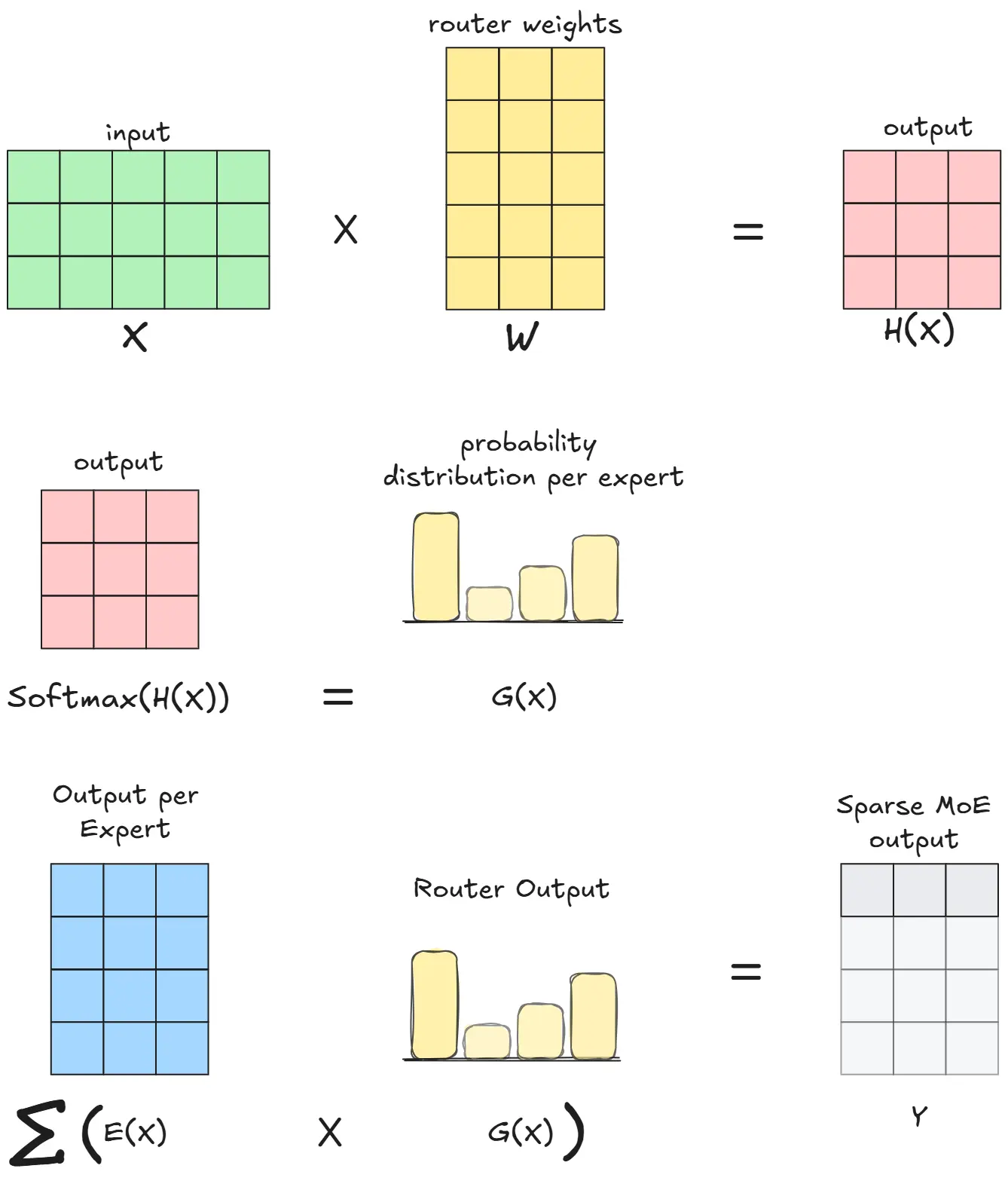
Image of MoE paper abstract

We begin with an input matrix X, multiple that by the router weights W. We take the softmax of this output to get the probability distribution $G(x)$. This is the likelihood of which experts are best for the given input.

Depending on how many experts we choose, we take the output of those experts and multiply that with the probability of that output begin chosen (This is done distriute the importance of the output based on which expert is most likely to be chosen). That gives us the output.

When we put it all together, this is how it looks.

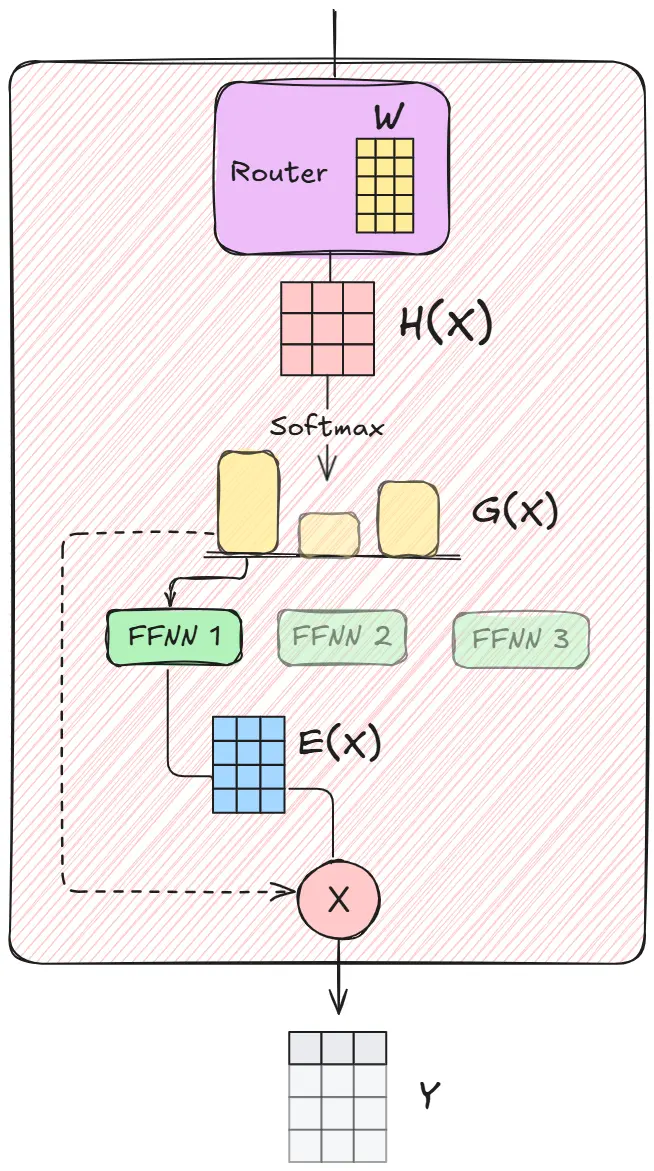
Image of MoE paper abstract

The original paper introduced two key innovations:

Softmax Gating (Dense Baseline)

# Simple dense gating - activates ALL experts with different weights
G(x) = Softmax(x · W_g)
y = Σ G(x)_i * Expert_i(x)  # All experts contribute

Noisy Top-K Gating (The Sparse Innovation)

# Step 1: Add trainable noise for load balancing
H(x)_i = (x · W_g)_i + StandardNormal() * Softplus((x · W_noise)_i)

# Step 2: Keep only top K experts, set others to -∞
KeepTopK(v, k)_i = {
    v_i    if v_i is in top k elements
    -∞     otherwise
}

# Step 3: Apply softmax (experts with -∞ get probability 0)
G(x) = Softmax(KeepTopK(H(x), k))

Why the noise? The Gaussian noise helps with load balancing. Without it, the same few experts would always dominate, creating a “rich get richer” problem where popular experts get more training and become even more popular.

Why Top-K? By keeping only the top K experts (typically K=2 or K=4), we achieve:

  • Sparsity: Most experts are inactive, saving computation
  • Specialization: Each expert focuses on specific patterns
  • Scalability: We can add thousands of experts without proportional compute increase
Addressing Performance Challenges

The paper identified several critical challenges that needed solving for MoE to work in practice:

The Shrinking Batch Problem

Original batch: 1024 examples
With 256 experts, k=4: Each expert sees only ~16 examples
Small batches = inefficient GPU utilization

Solution:

Mix Data and Model Parallelism

  • Combine batches from multiple GPUs before sending to experts
  • Each expert gets larger effective batch size: (batch_size * num_devices * k) / num_experts
  • Achieves factor of d improvement in expert batch size with d devices

Network Bandwidth Bottleneck

Modern GPUs have computational power thousands of times greater than network bandwidth. Meaning most time is spent between I/O operations.

Solution:

  • Keep experts stationary on devices (don’t move the experts)
  • Only send inputs/outputs across network (much smaller)
  • Use larger hidden layers to improve computation-to-communication ratio
To understand this better, consider reading Making Deep Learning Go Brrrr From First Principles

Load Balancing Problem

Without intervention, a few experts dominate while others are rarely used. This creates a vicious cycle: popular experts get more training data, become better, and thus get selected even more often. Meanwhile, neglected experts remain undertrained and essentially become dead weight.

Think of it like a classroom where only the brightest students get called on - they get more practice and become even brighter, while others stagnate.

The Dual Challenge

The paper identifies that we need to balance two distinct but related problems:

  1. Importance Imbalance: Some experts get high gating weights but few examples
  2. Load Imbalance: Some experts get many examples but low individual weights

Both scenarios are problematic. An expert with few high-weight examples overfits to specific patterns, while an expert with many low-weight examples receives weak learning signals.

Mathematical Solution: Auxiliary Loss

The authors introduce a load balancing loss that uses the coefficient of variation (CV) to measure and penalize imbalance:

\[CV = \frac{\sigma}{\mu} = \frac{\text{standard deviation}}{\text{mean}}\]

The CV is beautiful because it’s scale-invariant - it measures relative variability regardless of the absolute magnitudes. A CV of 0 means perfect balance, while higher values indicate increasing imbalance.

Step 1: Measuring Importance

Image of MoE paper abstract

For each expert $i$, we sum its gating probabilities across the entire batch:

\[\text{Importance}(X)_i = \sum_{x \in X} G(x)_i\]

This gives us the “importance scores” - how much each expert contributes regardless of which specific examples it processes.

Step 2: Computing the Importance Loss

\[\mathcal{L}_{\text{importance}} = w_{\text{importance}} \cdot CV(\text{Importance}(X))^2\]

Where: \(CV(\text{Importance}(X)) = \frac{\sigma(\text{Importance}(X))}{\mu(\text{Importance}(X))}\)

Why square the CV? This creates a stronger penalty for large imbalances and makes the gradient more well-behaved during optimization.

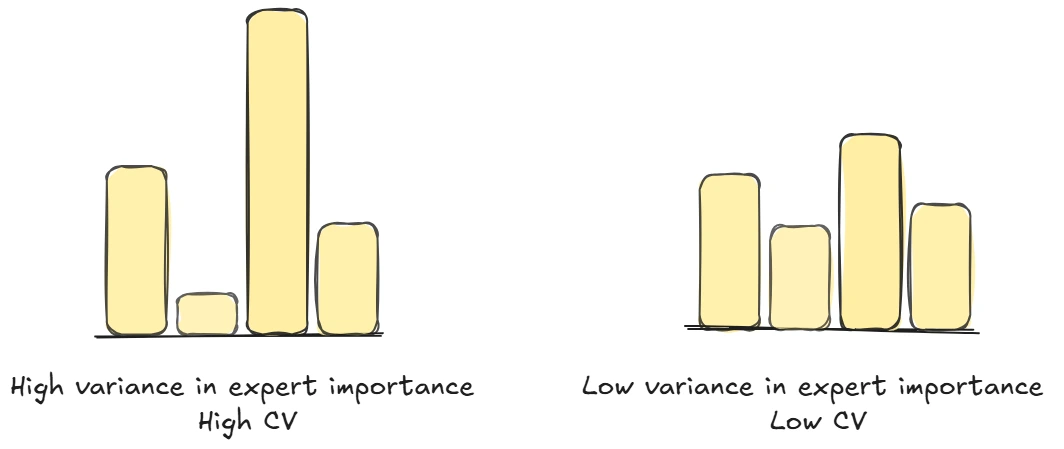
Image of MoE paper abstract

Step 3: Measuring Load

Load measures how many examples each expert actually processes:

\[\text{Load}(X)_i = \sum_{x \in X} \mathbf{1}[\text{expert } i \text{ is in top-k for } x]\]

In practice, this uses a smooth differentiable approximation rather than the hard indicator function.

Step 4: Computing the Load Loss

\[\mathcal{L}_{\text{load}} = w_{\text{load}} \cdot CV(\text{Load}(X))^2\]

The Complete Auxiliary Loss

\[\mathcal{L}_{\text{auxiliary}} = w_{\text{importance}} \cdot CV(\text{Importance}(X))^2 + w_{\text{load}} \cdot CV(\text{Load}(X))^2\]

Final Training Objective

\[\mathcal{L}_{\text{total}} = \mathcal{L}_{\text{main}} + \mathcal{L}_{\text{auxiliary}}\]

Why Both Losses Matter

Consider these scenarios:

  • Expert A: Gets selected for 100 examples with average weight 0.01 each
  • Expert B: Gets selected for 2 examples with average weight 0.5 each
  • Expert C: Gets selected for 50 examples with average weight 0.02 each

All have similar total importance (≈ 1.0), but vastly different training dynamics:

  • Expert A gets many weak signals → slow learning
  • Expert B gets few strong signals → overfitting risk
  • Expert C gets balanced signal → healthy learning

The dual loss ensures both the total contribution (importance) and the number of training examples (load) are balanced across experts.

Practical Impact

With proper load balancing:

  • All experts receive sufficient training signal
  • No expert dominates the computation
  • Model capacity is fully utilized
  • Training stability improves dramatically

This auxiliary loss was crucial for making MoE work at scale - without it, the models would collapse to using only a handful of experts, defeating the entire purpose of conditional computation.

Expert Capacity

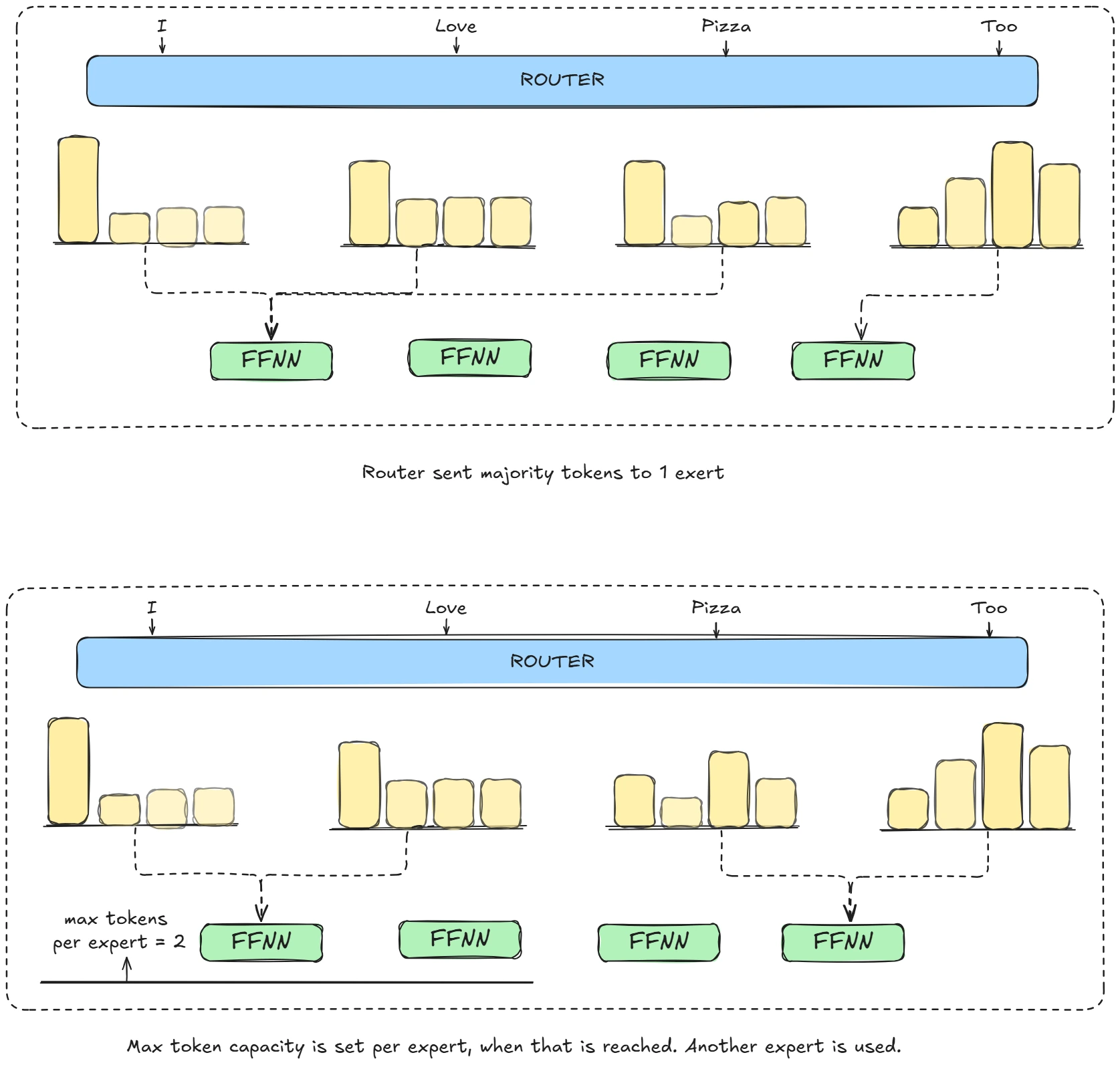
Image of MoE paper abstract

This wasn’t introduced in this paper, but let’s talk about it too since it’s crucial for modern MoE implementations. Even with perfect load balancing, there’s another challenge: token overflow. In the example above, FFNN 1 receives the majority of tokens. To prevent any single expert from being overwhelmed, we set an Expert Capacity - a maximum number of tokens each expert can process per batch. When an expert reaches capacity, additional tokens that would have been routed to it are either sent to the next-best expert or bypass the MoE layer entirely (called token overflow). This capacity mechanism ensures balanced computational load across experts and prevents memory bottlenecks, though it can sometimes mean tokens don’t get processed by their optimal expert. The trade-off between perfect routing and practical constraints is a key engineering challenge in scaling MoE systems.

Training the MoE Model

Key Challenge: How do experts specialize without explicit supervision?

The specialization emerges through training dynamics:

  1. Initial randomness: All experts start random and perform similarly
  2. Noise-induced preferences: The noise in gating creates slight preferences
  3. Reinforcement loop: Experts that perform well for certain inputs get selected more
  4. Emergent specialization: Through this process, experts develop distinct capabilities

What do experts actually learn? (From the paper’s analysis)

Image of tokens in MoE layre Image taken from Mistral paper

Unlike the intuitive “biology expert” or “math expert”, real MoE experts learn much more fine-grained patterns:

  • Syntactic specialization: Expert 381 specializes in contexts with “researchers”, “innovation”, and “technology”
  • Positional patterns: Expert 752 handles phrases where indefinite article “a” introduces important concepts
  • Semantic clustering: Expert 2004 focuses on contexts involving speed and rapid change

This emergent specialization is what makes MoE powerful - experts automatically discover useful divisions of labor without being explicitly told what to specialize in.

Revolutionary Results

Language Modeling (1B Word Benchmark):

  • 4096-expert MoE: 24% better perplexity than dense baseline
  • Same computational cost as much smaller dense models
  • Up to 137B parameters (1000x parameter increase) with minimal compute overhead
  • Training time: 12 hours vs weeks for equivalent dense models

Machine Translation (WMT’14):

  • En→Fr: 40.56 BLEU (vs 39.22 for GNMT)
  • En→De: 26.03 BLEU (vs 24.91 for GNMT)
  • Achieved new state-of-the-art with lower computational cost
  • Faster training than dense models with better quality

Computational Efficiency:

  • MoE models achieved 0.74-1.56 TFLOPS/GPU
  • Significant fraction of theoretical maximum (4.29 TFLOPS/GPU)
  • Only 37-46% of operations were in expert computations

The Breakthrough: This was the first time conditional computation delivered on its theoretical promise at scale. Previous attempts had struggled with the practical challenges that this paper solved.

From LSTMs to Modern Transformers

While this paper applied MoE to LSTMs (the dominant architecture in 2017), the core insights proved even more powerful when later applied to Transformers, about which we will learn more about in the later sections.

The path from this 2017 paper to modern LLMs shows how foundational ideas can have delayed but massive impact. Key lessons that influenced later work:

  1. Sparsity enables scale: The core insight that you can have orders of magnitude more parameters without proportional compute increase
  2. Load balancing is crucial: Without proper load balancing, MoE models fail to train effectively
  3. Engineering matters: Success required solving practical challenges like communication costs and batch sizing
  4. Specialization emerges: Given proper training dynamics, experts will naturally develop useful specializations

Today’s largest language models increasingly rely on MoE architectures, making this paper’s contributions more relevant than ever. The ability to scale to trillion-parameter models while maintaining reasonable training costs has become essential for pushing the boundaries of AI capabilities.

2018: BERT and Early Innovations

ULMFiT

Image of ULMFiT

Link to paper: Universal Language Model Fine-tuning for Text Classification

Quick Summary

This 2018 paper by Jeremy Howard and Sebastian Ruder introduces ULMFiT (Universal Language Model Fine-tuning), a method for transfer learning in NLP tasks. The authors present an approach that mirrors the success of transfer learning in computer vision by using a pre-trained language model and fine-tuning it for specific text classification tasks.

Key contributions:

  1. A three-stage approach to transfer learning for NLP tasks:

    • General-domain language model pretraining
    • Target task language model fine-tuning
    • Target task classifier fine-tuning

  2. Novel fine-tuning techniques to prevent catastrophic forgetting:

    • Discriminative fine-tuning (using different learning rates for different layers)
    • Slanted triangular learning rates (a specific learning rate schedule)
    • Gradual unfreezing (progressively unfreezing layers from last to first)

  3. State-of-the-art results on six text classification datasets with significant error reductions (18-24%)

  4. Impressive sample efficiency - with just 100 labeled examples, the method matches the performance of training from scratch with 10-100x more data

The paper demonstrates that effective transfer learning is possible in NLP without task-specific modifications or architecture changes, using a standard 3-layer LSTM model with careful fine-tuning techniques.


It is unfortunate that such an amazing paper which was a direct influence on the way GPT-1 was trained is often not talked about enough when it comes to LLM. Let’s do justice to that and understand more about Universal Language Model Fine-tuning or ULMFiT!!!

Problem

Inductive transfer learning has greatly impacted computer vision, but existing approaches in NLP still require task-specific modifications and training from scratch.

Before ULMFiT, transfer learning in NLP had a fatal flaw: catastrophic forgetting. When you fine-tuned a pretrained model on a new task, the model would rapidly “forget” its pretrained knowledge and overfit to the small target dataset. It was like teaching a polyglot to speak a new dialect, only to watch them forget all their other languages in the process.

This made transfer learning frustrating and often counterproductive. Researchers would get excited about pretrained models, only to find that fine-tuning destroyed the very knowledge they wanted to leverage.

Solution

ULMFiT, an effective transfer learning method that can be applied to any task in NLP, and introduce techniques that are key for fine-tuning a language model.

This paper laid crucial groundwork for the LLM revolution we see today.

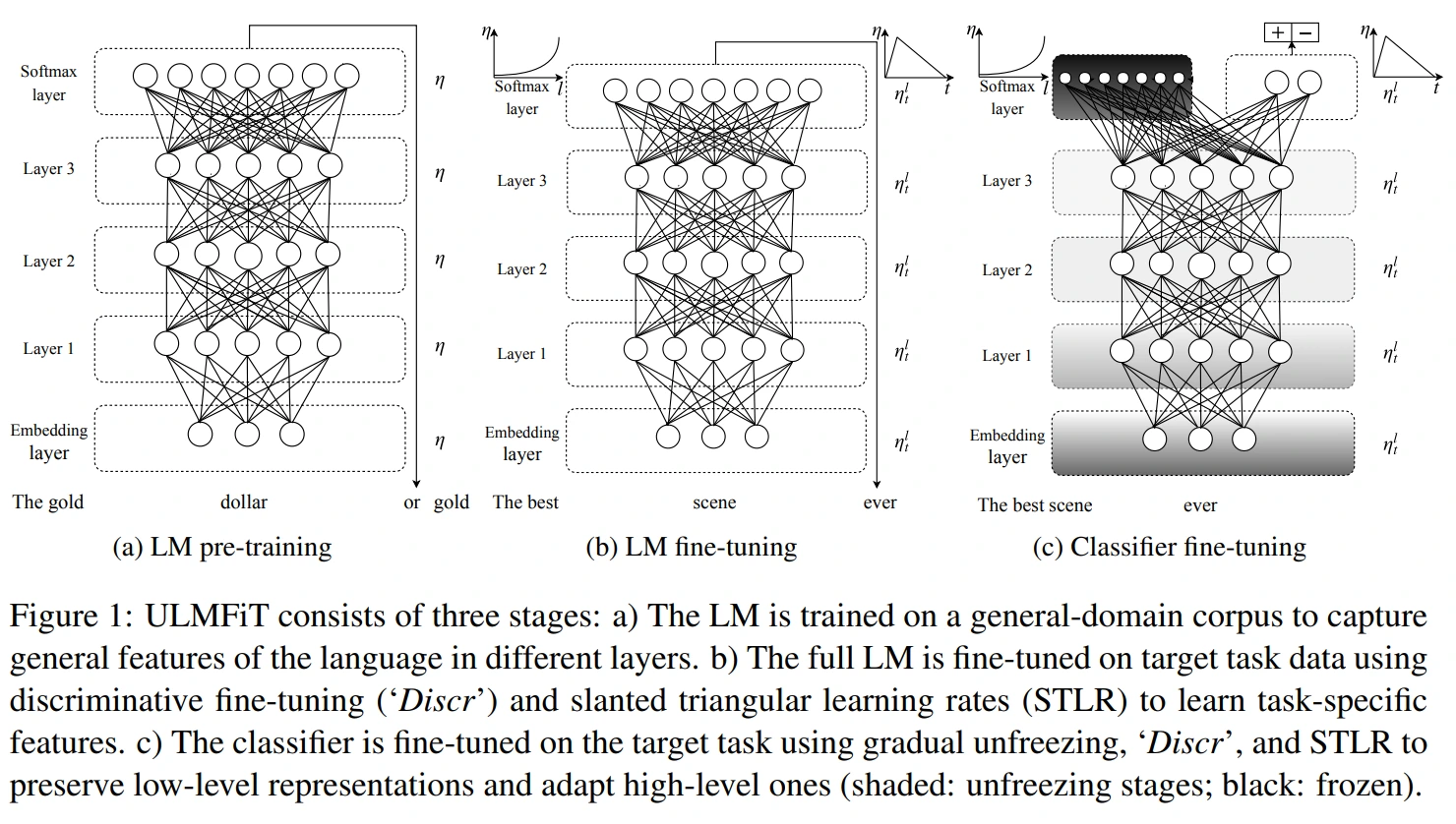
Image of ULMFiT training

The first stage is pretty basic and nothing innovative, but the second & third stage is where the innovation lies.

So far noone had been able to fine tune a general purpose model to perform well on target task which was not present in the original modeling of the original model

Why Transfer Learning Failed in NLP
Unlike computer vision, where you could take ImageNet features and achieve great results on new tasks, NLP models seemed to resist transfer. The problem wasn’t the models themselves but how we fine-tuned them. Traditional approaches used the same learning rate for all layers and froze nothing, causing rapid degradation of learned representations. ULMFiT’s breakthrough was realizing that different layers need different treatment during fine-tuning.

Let us understand each stage one by one

1st stage: General-domain LM pretraining

This is the simplest albeit the most expensive stage. Take a large dataset that has general information on many topics and train your model on it.

“We pretrain the language model on Wikitext-103 (Merity et al., 2017b) consisting of 28,595 preprocessed Wikipedia articles and 103 million words.”

This helps the model learn general language properties, At this stage it is nothing more than a really good next token predictor.

For example if you asked it the question

“What is the capital of France?”

Instead of getting Paris as the answer you will get. “What is the capital of India ?What is the captial of China” and so on.

That is where the innovative “fine-tuning” part comes in.

2nd Stage: Target task Language Model fine-tuning

Fine-tuning let us teach the LLM to follow our task specific requirements and control it’s behaviour in our target dataset.

Discriminative fine-tuning

In any deep neural network, different layers capture different parts of the dataset (This is a very popular article visualizing different parts of a CNN model). So it is reasonable to think that it won’t be a good idea to use the same learning rate to fine-tune each layer.

That is the idea behind discriminative fine-tuning. In this we have a different learning rate for each layer.

Stochastic Gradient Descent

\[\theta_t = \theta_{t-1} - \eta \cdot \nabla_\theta J(\theta)\]

Stochastic Gradient Descent with different learning rate for each layers

\[\theta_t^l = \theta_{t-1}^l - \eta^l \cdot \nabla_{\theta^l} J(\theta)\]

The authors found that it’s best to first find the optimum $\eta^L$ for the last layer, then go downstream following this rule $\eta^{l-1} = \eta^l/2.6$

Slanted triangular learning rates

When fine-tuning a pretrained model, we face a fundamental tension. We want the model to quickly adapt to our target task, but we also need to preserve the valuable knowledge it learned during pretraining. Fixed learning rates can’t solve this dilemma.

To solve that the authors introduced STLR, an adaptive learning rate that changes with number of iterations.

The idea is, start with a higher learning rate to rapidly adapt the model to the target task’s patterns, then gradually decrease it to fine-tune without destroying pretrained representations.

Image of STLR

Think of it like learning to drive in a new city. Initially, you drive faster to quickly get oriented and find the general area you need. Once you’re close to your destination, you slow down to carefully navigate the final streets and parking.

This was achieved using the following formula

\[\text{cut} = \lfloor T \cdot \text{cut\_frac} \rfloor\] \[p = \begin{cases} t/\text{cut}, & \text{if } t < \text{cut} \\ 1 - \frac{t-\text{cut}}{\text{cut} \cdot (1/\text{cut\_frac} - 1)}, & \text{otherwise} \end{cases}\] \[\eta_t = \eta_{\max} \cdot \frac{1 + p \cdot (\text{ratio} - 1)}{\text{ratio}}\]

Where:

  • $T$ is the total number of training iterations
  • $\text{cut_frac}$ is the fraction of iterations for learning rate increase (typically 0.1)
  • $\text{cut}$ is the iteration where we switch from increasing to decreasing
  • $p$ is the fraction of iterations in current phase
  • $\text{ratio}$ specifies how much smaller the lowest LR is from maximum (typically 32)
  • $\eta_{\max}$ is the maximum learning rate (typically 0.01)
  • $\eta_t$ is the learning rate at iteration $t$
3rd Stage: Target task classifier fine-tuning

The final stage adds a classifier head to the fine-tuned language model and trains it for the specific task. This stage introduces several crucial techniques that prevent the model from forgetting its pretrained knowledge.

Gradual Unfreezing

Image of Gradual Unfreezing

Rather than fine-tuning all layers at once, which risks catastrophic forgetting, ULMFiT gradually unfreezes layers starting from the last layer. The intuition is elegant: the last layers contain the most task-specific knowledge, while early layers capture universal language features that should change slowly.

The process works like this: First, unfreeze only the classifier head and train for one epoch. Then unfreeze the next layer down and continue training. Repeat this process until all layers are unfrozen. This gradual approach gives the model time to adapt each layer’s representations smoothly without destroying the foundation built in earlier layers.

Concat Pooling

Image of Concat Pooling

ULMFiT also introduced concat pooling for text classification. Instead of using only the final hidden state, it concatenates the last hidden state with both max-pooled and mean-pooled representations across all timesteps. This captures information from the entire document, not just the end.

BPTT for Text Classification (BPT3C)

Image of BPT3C

For handling long documents, ULMFiT adapts backpropagation through time by dividing documents into fixed-length batches while maintaining hidden state continuity between batches.

Revolutionary Results

ULMFiT’s results were unprecedented for their time. On six text classification datasets, the method achieved 18-24% error reduction compared to state-of-the-art approaches. More impressively, with just 100 labeled examples, ULMFiT matched the performance of training from scratch with 10-100× more data.

This sample efficiency was the real game-changer. Suddenly, high-quality NLP became accessible to domains with limited labeled data, democratizing the field in ways that hadn’t been possible before.

ELMo: Embeddings from Language Models

Image of ELMo

Link to paper: Deep contextualized word representations

Quick Summary

This paper introduces ELMo (Embeddings from Language Models), a new approach to creating word representations that capture both complex word characteristics (syntax and semantics) and how those characteristics change across different contexts (addressing polysemy). Unlike traditional word embeddings that assign a single vector per word, ELMo derives representations from a bidirectional language model (biLM) pre-trained on a large text corpus.

The key innovation is that ELMo representations are deep - they’re a function of all internal layers of the biLM, not just the final layer. The authors show that different layers capture different linguistic properties (lower layers capture syntax, higher layers capture semantics). By learning task-specific weightings of these layers, models can access both types of information simultaneously.

The authors demonstrate that adding ELMo to existing models significantly improves performance across six diverse NLP tasks, including question answering, textual entailment, sentiment analysis, and named entity recognition - achieving state-of-the-art results in all cases, with relative error reductions ranging from 6-20%.


Embeddings are a vital part of LLMs, because they determine the very understanding of tokens. Think of them as the language that allows machines to understand and work with human text. Just like how we might describe a person using various characteristics (height, age, personality), embeddings describe words using hundreds of numerical features that capture their meaning, relationships, and usage patterns.

Problem

Before ELMo, word embeddings had a major limitation: each word had only one representation regardless of context. The word “bank” would have the same vector whether you’re talking about a financial institution or the side of a river. This is called the polysemy problem - one word, multiple meanings, but only one embedding.

learning high quality representations can be challenging. They should ideally model both (1) complex characteristics of word use (e.g., syntax and semantics), and (2) how these uses vary across linguistic contexts (i.e., to model polysemy).

Solution

ELMo’s breakthrough was making embeddings contextual. Instead of giving “bank” the same representation everywhere, ELMo creates different representations based on the surrounding words. When “bank” appears near “loan” and “mortgage,” it gets a finance-related representation. When it appears near “river” and “water,” it gets a geography-related representation.

Our representations differ from traditional word type embeddings in that each token is assigned a representation that is a function of the entire input sentence. We use vectors derived from a bidirectional LSTM that is trained with a coupled language model (LM) objective on a large text corpus.

Before we start talking about ELMo we have to understand how word embeddings work and what they are. You can skip this section if you have an extensive understanding of the topic at hand

This book proved to be extremely helpful while writing this section.

Traditional Word Embeddings

Machines do not understand text but rather numbers. So researchers have come up with ways to represent words as numbers that still captures their complexity, semantics, meaning etc. Let’s go one by one.

One-Hot Vectors

One of the simplest solution is to create one hot encoding for each word.

Image of One Hot Vector

Here, every word has been assigned a unique vector and the length of our one-hot encoded vector would be equal to the size of $V$ ($|V| = 3$).

Note:

  • In OHE words are independant of each other and hence do not capture any relationship between them
  • OHE is computationally expensive as in reality the size of vocabulary can be in billions

Bag-of-Words (BOW)

Think of BOW as the most straightforward way to convert text into numbers - it’s like counting how many times each word appears in a document, completely ignoring the order.

BOW creates a document-term matrix where each row represents a document and each column represents a word from our vocabulary. Each cell contains the frequency of that word in that specific document.

# Simple BOW implementation
documents = ['this is the first document',
             'this document is the second document',
             'this is the third one',
             'is this the first document']

# Create vocabulary
vocab = []
for doc in documents:
    for word in doc.split():
        if word not in vocab:
            vocab.append(word)

# Create BOW matrix
bow_matrix = []
for doc in documents:
    word_count = [doc.split().count(word) for word in vocab]
    bow_matrix.append(word_count)

print("Vocab:", vocab)
print("BOW Matrix:", bow_matrix)

# Vocab:
# ['this', 'is', 'the', 'first', 'document', 'second', 'third', 'one']

#BOW Matrix:
# [[1, 1, 1, 1, 1, 0, 0, 0],
#  [1, 1, 1, 0, 2, 1, 0, 0],
#  [1, 1, 1, 0, 0, 0, 1, 1],
#  [1, 1, 1, 1, 1, 0, 0, 0]]

The problem? BOW treats “The cat sat on the mat” and “The mat sat on the cat” as identical because it only cares about word counts, not context or order. Plus, common words like “the” and “is” get the same weight as meaningful words.

Co-occurrence Matrix

Instead of just counting words in documents, what if we count how often words appear together? That’s exactly what co-occurrence matrices do.

A co-occurrence matrix shows how frequently word pairs appear within a defined window (like within the same sentence). If “learning” and “machine” often appear together, they’ll have a high co-occurrence score.

Image of One Hot Vector

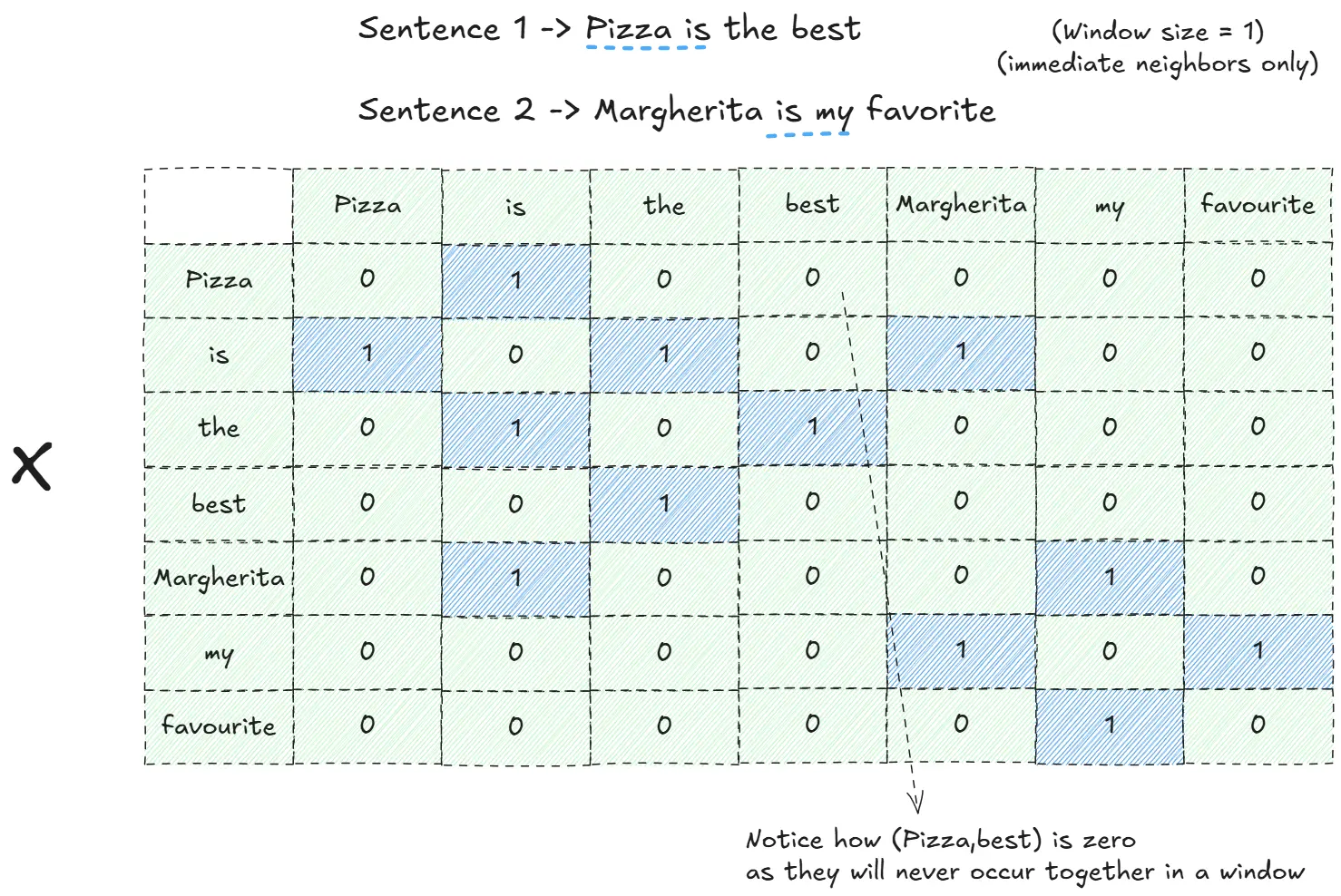
The mathematical representation: For words $w_i$ and $w_j$, the co-occurrence count $C_{ij}$ represents how many times they appear together within a context window.

\[C_{ij} = \sum_{k=1}^{N} \mathbb{I}(w_i, w_j \text{ co-occur in context } k)\]

Where $\mathbb{I}$ is an indicator function and $N$ is the total number of contexts.

# Simple co-occurrence matrix
def build_cooccurrence_matrix(documents, window_size=1):
    # Flatten all documents into one list
    all_words = []
    for doc in documents:
        all_words.extend(doc.split())

    # Create vocabulary
    vocab = list(set(all_words))
    vocab_size = len(vocab)

    # Initialize matrix
    cooc_matrix = [[0 for _ in range(vocab_size)] for _ in range(vocab_size)]

    # Count co-occurrences
    for i in range(len(all_words)):
        target_word = all_words[i]
        target_idx = vocab.index(target_word)

        # Check words within window
        for j in range(max(0, i-window_size), min(len(all_words), i+window_size+1)):
            if i != j:
                context_word = all_words[j]
                context_idx = vocab.index(context_word)
                cooc_matrix[target_idx][context_idx] += 1

    return cooc_matrix, vocab

The beauty of co-occurrence matrices is that they capture some semantic relationships - words that often appear together likely have related meanings.

N-Gram

N-grams extend the BOW concept by considering sequences of $n$ consecutive words instead of individual words. This helps capture some word order and context.

  • Unigrams (n=1): Individual words → [“this”, “is”, “the”, “first”]
  • Bigrams (n=2): Word pairs → [“this is”, “is the”, “the first”]
  • Trigrams (n=3): Word triplets → [“this is the”, “is the first”]

The mathematical formulation for n-gram probability: \(P(w_n|w_1, w_2, ..., w_{n-1}) \approx P(w_n|w_{n-k+1}, ..., w_{n-1})\)

def generate_ngrams(text, n):
    words = text.split()
    ngrams = []
    for i in range(len(words) - n + 1):
        ngram = ' '.join(words[i:i+n])
        ngrams.append(ngram)
    return ngrams

The trade-off? Higher n-values capture more context but create exponentially more features and become computationally expensive.

TF-IDF (Term Frequency-Inverse Document Frequency)

TF-IDF is the smart cousin of BOW. It doesn’t just count words - it considers how important a word is to a specific document relative to the entire collection.

The intuition: Words that appear frequently in one document but rarely across all documents are more significant for that specific document.

\[\text{TF-IDF}(t,d) = \text{TF}(t,d) \times \text{IDF}(t)\]

Where:

  • $\text{TF}(t,d) = \frac{\text{count of term } t \text{ in document } d}{\text{total words in document } d}$
  • $\text{IDF}(t) = \log\left(\frac{\text{total documents}}{\text{documents containing term } t}\right)$
import numpy as np
import pandas as pd

documents_name = ["Document-1", "Document-2", "Document-3", "Document-4"]

documents = ['this is the first document',
             'this document is the second document',
             'this is the third one',
             'is this the first document']

word_tokens = []

for document in documents:
    words = []
    for word in document.split(" "):
        words.append(word)
    word_tokens.append(words)

vocab = set()

for document in word_tokens:
    for word in document:
        vocab.add(word)

vocab = list(vocab)

TF = [[0 for j in range(len(vocab))] for i in range(len(word_tokens))]

for i, document in enumerate(word_tokens):
    for word in document:
        j = vocab.index(word)
        TF[i][j] += 1 / len(word_tokens[i])

idf = [0 for i in range(len(vocab))]
D = len(word_tokens)

for j, word_vocab in enumerate(vocab):
    df = 0
    for document in word_tokens:
        for word in document:
            if word_vocab == word:
                df += 1
                break
    idf[j] = np.log(D/df)

TFIDF = [[0 for j in range(len(vocab))] for i in range(len(word_tokens))]

for i in range(len(word_tokens)):
    for j in range(len(vocab)):
        TFIDF[i][j] = TF[i][j] * idf[j]

data = pd.DataFrame(TFIDF, columns=vocab, index=documents_name).round(3)
data

Code taken from here

if we calculate tf-idf of the same example as before we get an output like below

Image of One Hot Vector

Notice how common words like “this”, “is”, “the” get lower TF-IDF scores because they appear in most documents, while specific words like “second” or “third” get higher scores.

The Limitation of Traditional Embeddings

All these methods share a fundamental flaw: they assign the same representation to a word regardless of context. The word “bank” gets the same vector whether we’re talking about a river bank or a financial institution. This is where contextual embeddings like ELMo come to the rescue.

Static Word Embeddings

Word2Vec

The following are excellect sources to understand Word2Vec in a deeper level. Consider going through them

Intuition

We are going to start with the old and cheesy explanation of Word2Vec. Talking about similarity of vector representation in space. (If you do not understand what I am talking about, Most explanations of Word2Vec use the explanation I am about to give. Fret not, for we will dive deeper too!)

I absolutely love cheese. And I have scale in which I measure how cheesy a piece of cheese is. Image of Word2Vec explanation

Anytime I find a new cheese, I taste it and put it on my scale. I use this scale to choose which cheese to eat based on my mood.

Image of Word2Vec ex5planation

But one day I ran into a cheese (yellow cheese) which had the same cheesiness as the white cheese. Now how do I differentiate between the two? well cheese has many other properties (or features from the ML perspective). Like protein!!

Image of Word2Vec explanation

I can add that as another axis and I can use that as another metric to choose the kind of cheese I want to eat.

Image of Word2Vec explanation

This way of plotting cheese based on different properties provides with another amazing way. One day a friend of mine came and said he really liked red cheese, but I was out of red cheese :( because I love it too.

So I can just find the cheese which is most similar to it, using cosine similarity!!

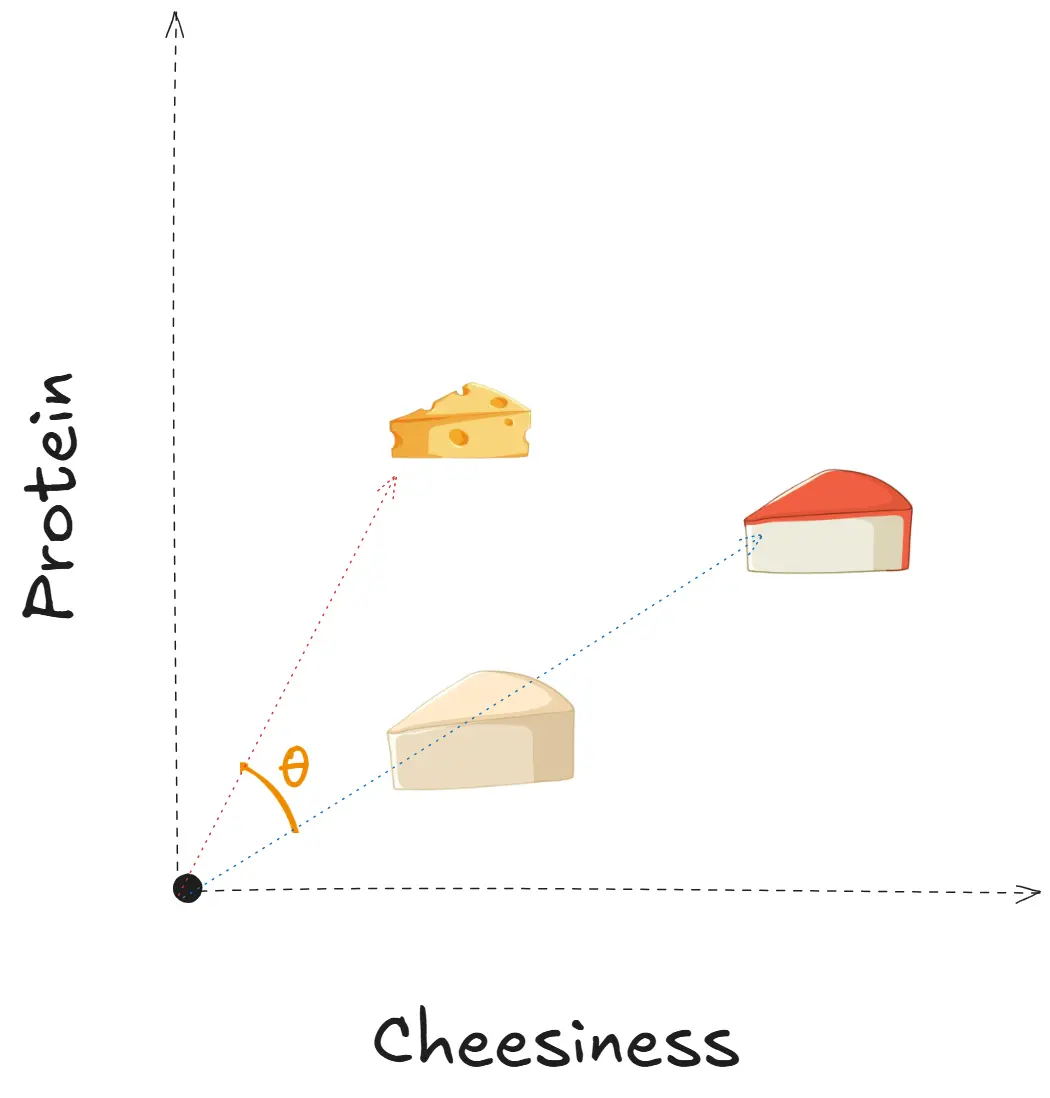
Image of Word2Vec explanation

That is essentially the idea of Word2Vec, We plot multiple words in an n dimensional space (I used 2 dimensional because I can plot it. I can’t plot a 7d space, I will love to meet you if you can tho!!!). And find similar words based on cosine similarity.

The cosine similarity between two vectors A and B is calculated as:

\[\cos(\theta) = \frac{A \cdot B}{||A|| ||B||} = \frac{\sum_{i=1}^{n} A_i B_i}{\sqrt{\sum_{i=1}^{n} A_i^2} \sqrt{\sum_{i=1}^{n} B_i^2}}\]

This gives us a value between -1 and 1, where 1 means the vectors point in exactly the same direction (very similar), 0 means they’re perpendicular (unrelated), and -1 means they point in opposite directions (very different).

There is a popular example that shows the distance between king and woman is same as the distance between man and woman. This essentially shows that both the pair of words share very similar ideas with only a few differences (maybe in royalty).

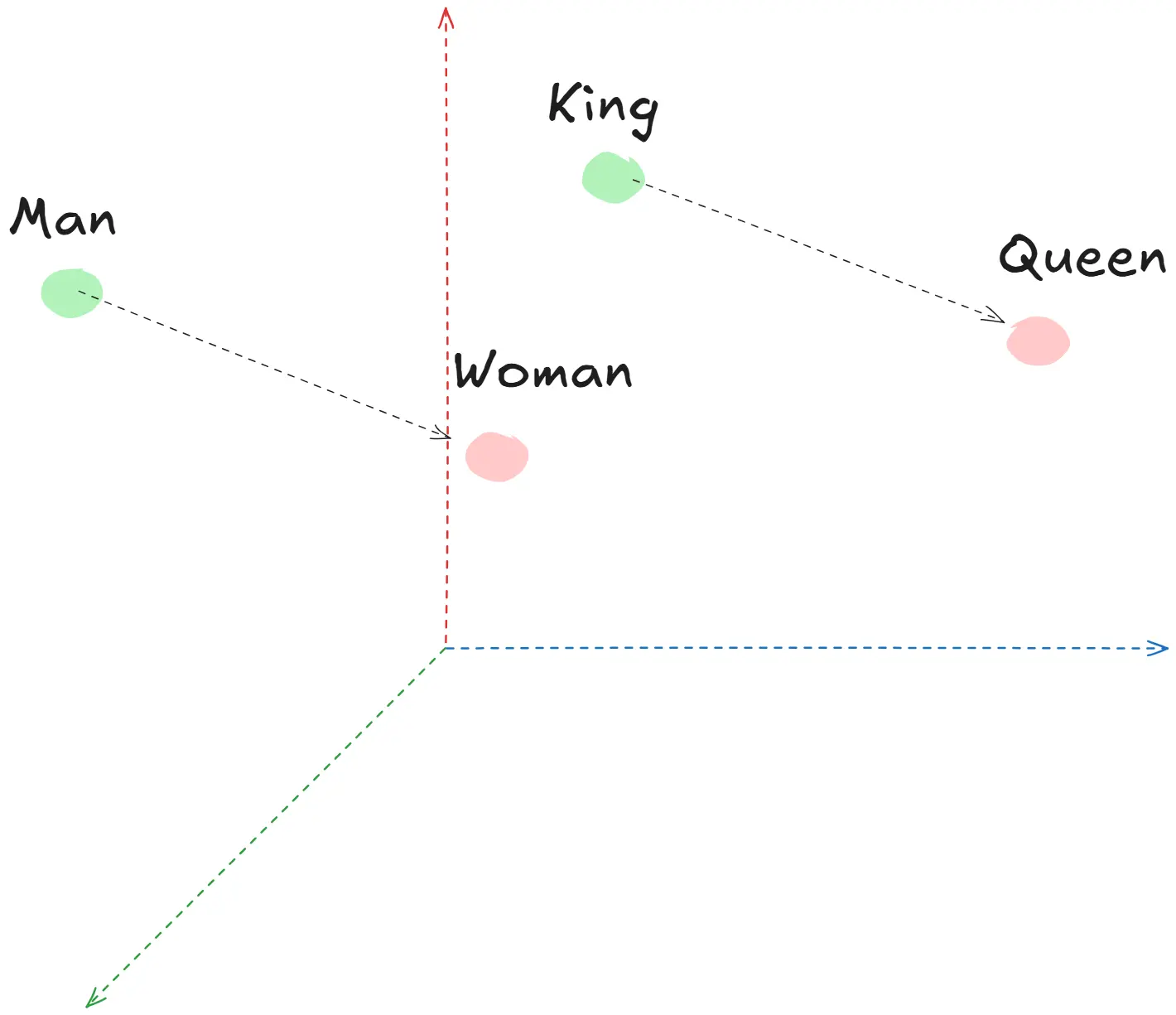
Image of Word2Vec explanation

In reality Word2Vec looks something more like the below image (ouch!!).

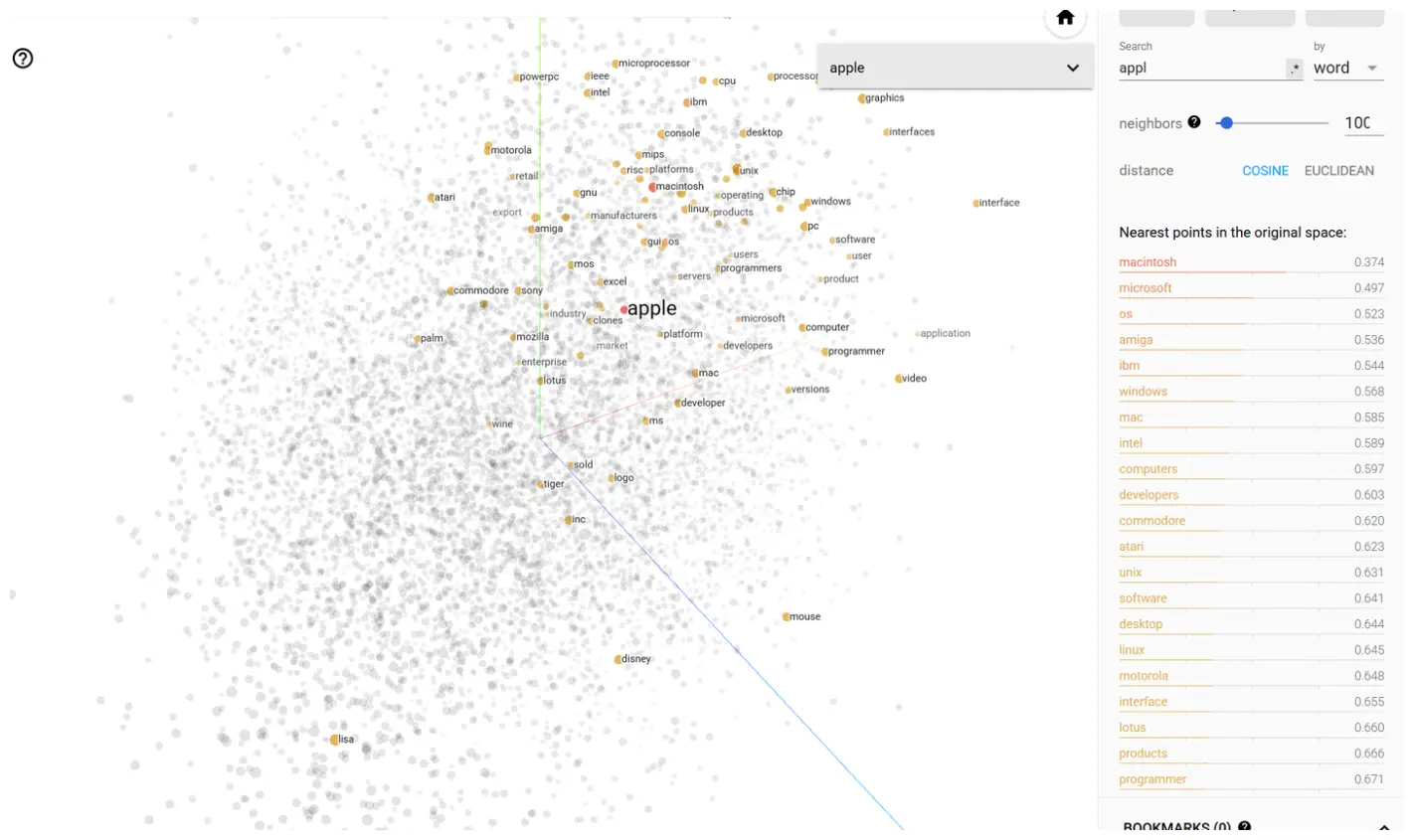Image of Word2Vec explanation Image taken from Embedding Projector

Skip gram model

Now that we understand the idea behind Word2Vec, it’s time to understand how it is implemented. I will be skipping Continous Bag of words, an idea introduced in the original paper as it is not essential in my opinion. You can read more about it in the sources I have provided.

Skip gram in 1 sentence -> Given a word, find it’s nearby words (context words).
CBOW in 1 sentence -> Given context words, find the target word.

One of the many beautiful thing about NLP is, you can create a labelled dataset using an unlabelled dataset. Our objective is to build a model that finds words nearby a target word.

Let us understand how the training dataset is created using a sample sentence. We first define a window (here it’s 2), we have our target word with the relevant context words around it.

Image of Word2Vec explanation

Now that we have our training data, let us understand how the model itself is constructed. Remember how we talked about cheesiness as a feature for our cheese, then protein, well both of them can be described as their own individual neuron. So in the example below we have an embedding model with 300 as it’s dimension (In modern embedding model when you talk about dimensions, it is essentially talking about how many features can be used to describe one particular token, as a rule of thumb higher the dimension, more complex is it’s representation)

So for any given word, we can create a one hot encoding, then pass it through our embedding model. Which is then passed to the final Softmax layer which gives the probability of all the words which are likely to be a context word.

I have a question for you, What is the difference between nn.Embedding and nn.Sequential?

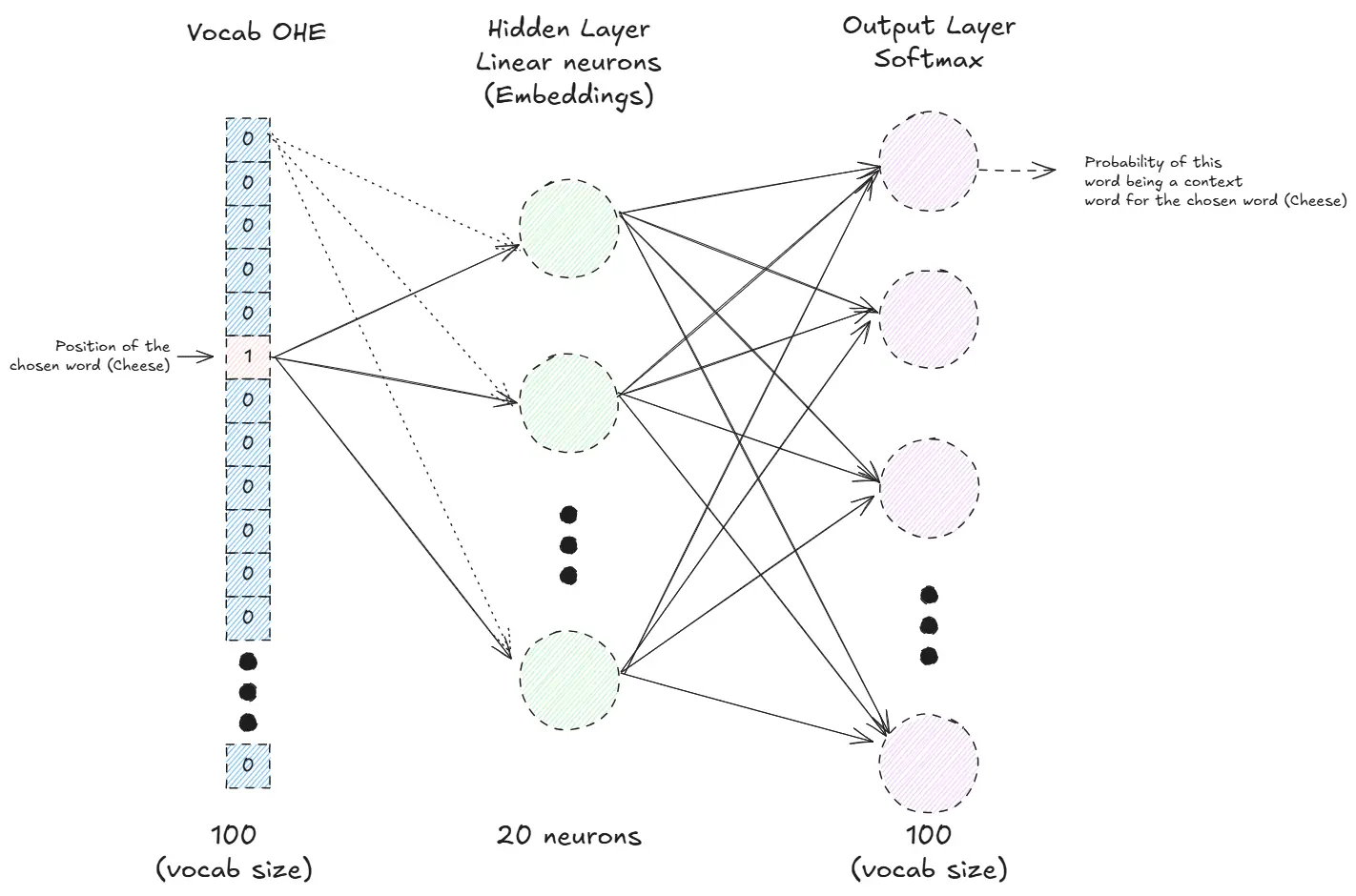
Image of Word2Vec explanation

One thing I found interesting was, we talk about “Embedding Matrix” but the above image describes a typical neural network model, what is going on over here?

Well if we look below, it becomes much easier to understand. The word vector represents the OHE encoding of the chosen work.

Each row of the embedding matrix represents the weights of every word in that neuron. So when we do a matrix multiplication, we get the weight for that word from different neurons.

It’s easier to visualize as different embedding vectors for each token of a fixed dimension.

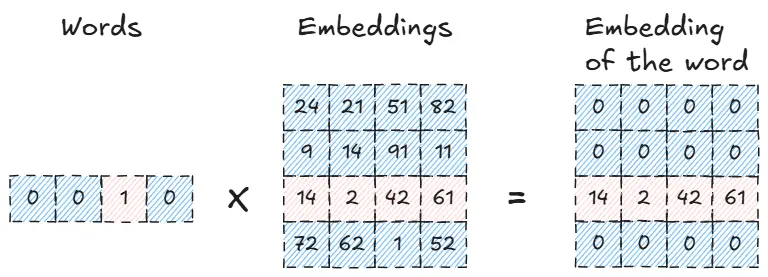
Image of Word2Vec explanation

Now we just run a training loop and voila, the hidden layer, is our embedding matrix. But we have a problem. As this was an example we used a vocabulary of a 100 words, but in reality the vocabulary is 100x times larger. And calculating softmax of so many tokens is a very expensive operation.

imagine a vocabulary of 10,000 tokens (quite small from modern vocabs) with 500 dimensional embedding model. That’s 5 million training parameter!!!

There are a few solutions proposed by the researchers to overcome this problem. Interestingly the original paper only mentions Hierarical Softmax, but the code shared by researches talks about sub-sampling and Negative Sampling. So let’s talk about all three!

[UPDATE] I later found out that they introduced these ideas in there follow up paper here. (Have a look at the authors… it is something haha)

This blog covered the mentioned topics quite well and I have taken inspiration from it while writing this section.

Sub-Sampling

Image of Word2Vec explanation

If we look at one particular example from our dataset generation step, particularly the 3rd line. We will see that is is a word that must be quite common in sentences. And hence we can expect to run into many pairs of is, ...

To fix this problem, the authors introduced a sampling rate.

\[P(w_i) = 1 - \sqrt{t/f(w_i)}\]

Where $f(w_i)$ is the frequency of the word and $t$ is a chosen threshold.

Negative Sampling (better for frequent words, better with low dimensional vectors)

The idea is quite interesting, If we go back to the example that we started with. I.e training on a vocab of 100 words. Our main problem was that it was very expensive to calculate the softmax of so many tokens.

So what if instead of training on all the tokens, we took a small subset of the negative samples. I.e tokens which are not related to our target word, and take a bunch of context words. And train it using logistic regression. In other words, tell if two words are neighbours or not.

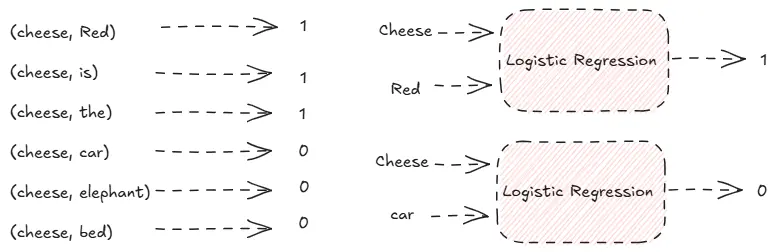
Image of Word2Vec explanation

This greatly simplifies training, and reduces the cost significantly too. One interesting thing to note is the authors used a unigram distribution to pull the negative samples out of.

\[P(w_i) = {f(w_i)}^{3/4}/\sum({f(w_i)}^{3/4})\]

If you wish to learn more about negative sampling consider reading this.

I find “why this even works” more interesting than the fact that it works (And this produces better results than our original method). It’s actual name is noise contrastive estimation and the way I imagine it is, we are pulling similar words together while pushing dissimilar words away. Now if we pushed all of the dissimilar words away as we were doing we inevitably pushed away similar words for different pairs too.

Consider reading about contrastive loss. (This is a good medium article on the topic, Consider looking at the author of contrastive loss too… it’s somehting haha)

Hierarical Softmax (better for infrequent words)

Let’s start with an example, because that really drives the idea home.

“I can have pizza every day”

If we used the standard softmax to calculate the probability of “pizza” given some context, we would do something like:

\[P(pizza|context) = \frac{e^{v'_{pizza} \cdot h}}{\sum_{w \in V} e^{v'_w \cdot h}}\]

Where $h$ is the hidden layer output (context vector) and $v’_w$ are the output embeddings.

But Hierarchical Softmax constructs a binary tree and we get a structure like below:

Image of Word2Vec explanation

Understanding how the binary tree is constructed is beyond the scope of this article, but if you understand how Huffman Encoding works, that is one way of creating the tree. More frequent words get shorter paths, less frequent words get longer paths.

The equation then becomes:

\[P(pizza|context) = \sigma(v'_{root} \cdot h) \times \sigma(-v'_{n_1} \cdot h) \times \sigma(v'_{n_4} \cdot h)\]

Where:

  • $\sigma(x) = \frac{1}{1 + e^{-x}}$ is the sigmoid function
  • $v’_{n_i}$ are the learned vectors for internal nodes
  • The negative sign appears when we take the left branch at a node

This reduces the computation from $O(|V|)$ to $O(\log|V|)$, where $V$ is the size of the vocabulary.

If you wish to learn more about Hierarchical Softmax consider reading this blog.

GloVe

This blog helped me considerably while writing this section.

GloVe stands for Global Vectors for Word Representation, it is seemingly an improvement over Word2Vec as it considers global statistics over local statistics.

Well what does that mean? Put simply, we leverage the global co-occurrence matrix instead of using a local context window like we did in Word2Vec.

The main innovation behind GloVe is the idea that we only need to calculate the ratio of probability of the occurrence of two words to capture their semantic relation. This ratio-based approach helps filter out noise from non-discriminative words and highlights meaningful relationships.

First we create a co-occurrence matrix $X$ based on the available corpus. The notation $X_{ij}$ refers to number of times word j has appeared in the context of word i. We calculate the probability of a word j occurring given i as $P(j|i) = X_{ij}/X_i$, where $X_i$ is the sum of all co-occurrence counts for word i (i.e., $X_i = \sum_k X_{ik}$).

Image of Word2Vec explanation

Let’s understand it with an example.

We created the co-occurrence matrix for two sentences “Pizza is the best” and “Margherita is my favorite” using a window size of 1 (immediate neighbors only).

Let’s calculate the probability of “Pizza” given “is” (this is from a very small corpus only to show how it is calculated, it is not reminiscent of the actual results).

From our matrix, “is” co-occurs with three words: “Pizza” (1 time), “the” (1 time), and “Margherita” (1 time). So the total count for “is” is 3.

\[P(\text{Pizza}|\text{is}) = \frac{X_{\text{is,Pizza}}}{X_{\text{is}}} = \frac{1}{3} = 0.33\]

Image of Word2Vec explanation Image taken from the original paper

If we look at the example provided by the authors from a real corpus, the power of ratios becomes clear. It is pretty intuitive that $P(solid|ice)$ will have a higher value than $P(solid|steam)$, because “solid” is more likely to appear in the context of “ice” than “steam”. Hence their ratio $P(solid|ice)/P(solid|steam) = 8.9$ has a large value, indicating “solid” is discriminative for “ice”.

For “gas”, we see the opposite: $P(gas|ice)/P(gas|steam) = 0.085$, a small ratio indicating “gas” is discriminative for “steam”.

Whereas for “water”, both ice and steam are likely to co-occur with it, so the ratio $P(water|ice)/P(water|steam) = 1.36$ is close to 1, indicating “water” doesn’t discriminate between ice and steam. More interesting is “fashion” with a ratio of 0.96 ≈ 1, because both ice and steam are unlikely to be related to fashion. This ratio-based approach elegantly filters out such neutral co-occurrences that don’t provide semantic information.

This insight - that ratios of co-occurrence probabilities capture semantic relationships better than raw probabilities - forms the mathematical foundation of GloVe’s log-bilinear regression model.

To understand more about the implementation and training details, consider reading the original paper and this article.

I have skipped a lot of the different parts, like training, eval, results etc. Because this is ultimately a section on ELMo and not GloVe. But the idea is fascinating enough to garner some time spent on it.

Contextual Word Embeddings

Embeddings from Language Models (ELMo)

We more or less now have a complete understanding of how different embedding models work, so it’s time to understand the model of the hour: ELMo.

There are two things we need to understand: how it’s trained and how it’s used.

Training is quite simple - we train a two-layer bi-directional LSTM on a Language Modeling task.

The Language Modeling task basically means: given all these words, what’s the most likely word that comes next? It is exactly how GPT-1 was trained, which we will be covering next.

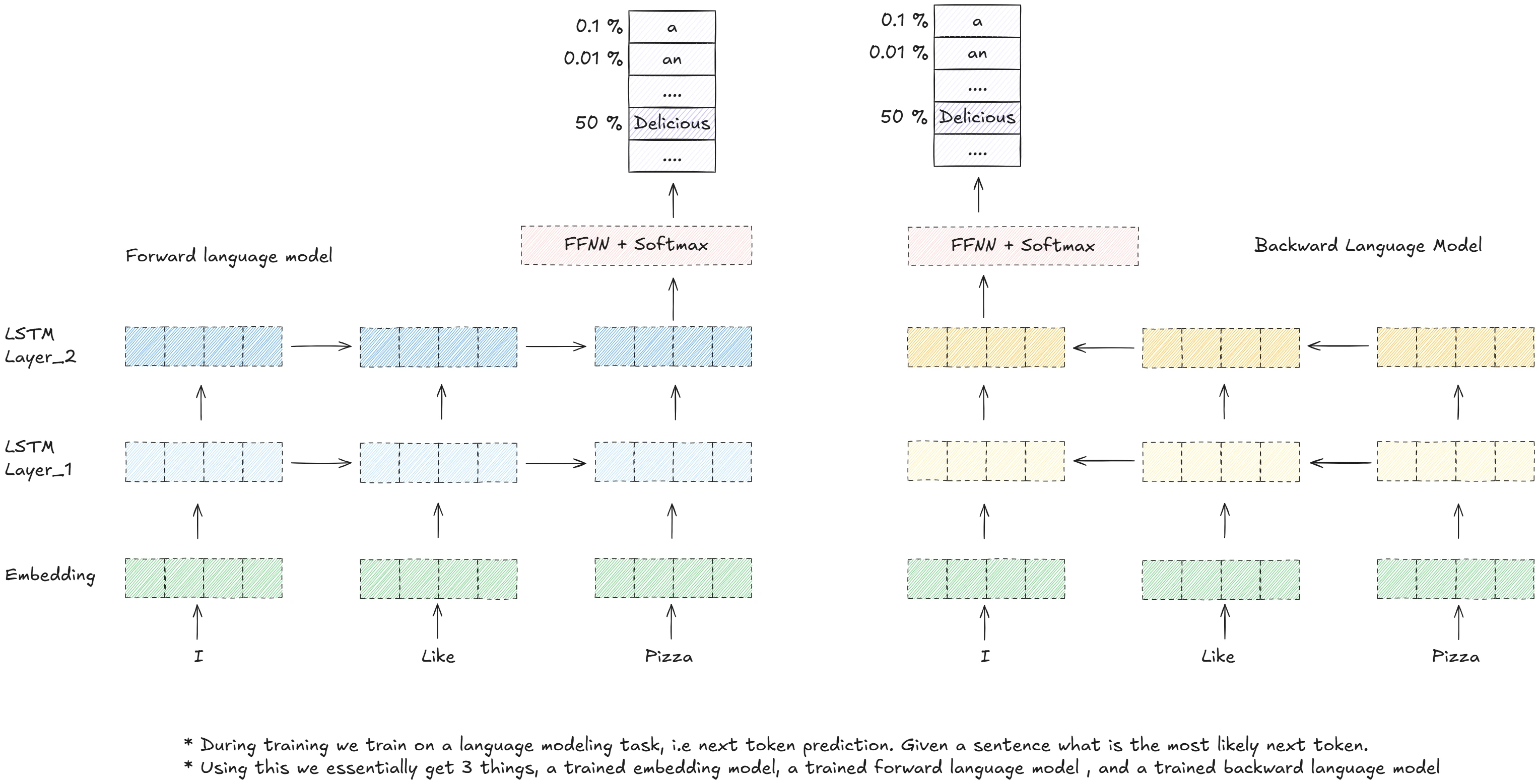Image of Word2Vec explanation image inspired from this blog

Now I had a question while reading this: ELMo is an embedding model, right? But what we are doing is next token prediction here. How is it used with other NLP models then? If you have the same question, you are on the right track. It is quite an innovative solution in my opinion.

Let us first start with the very essence of any NLP task: We begin with a sentence, right? We can use this sentence, pass it to our trained ELMo model, and extract representations from different layers. The key insight is that we don’t just use the final layer - we combine representations from all layers (character embeddings + both LSTM layers) using learned weights.

Image of Word2Vec explanation

We can then give these combined embeddings to any other NLP model. Voila! This understanding will prove to be extremely useful as we move to bigger LLMs. While modern embedding models don’t use ELMo’s specific bidirectional LSTM approach, ELMo’s key innovation of contextual embeddings and the concept of using pre-trained language models for embeddings laid the groundwork for today’s transformer-based embedding models.

GPT-1

Image of GPT-1

Link to paper: Improving Language Understanding by Generative Pre-Training , blog

Quick Summary

This seminal 2018 paper from OpenAI researchers (Radford, Narasimhan, Salimans, and Sutskever) introduces a powerful semi-supervised approach to natural language understanding that combines unsupervised pre-training with supervised fine-tuning.

The key innovation lies in training a large transformer-based language model on unlabeled text data, then leveraging the learned representations by fine-tuning this model on specific downstream tasks. This approach addresses a fundamental challenge in NLP: the scarcity of labeled data for various language understanding tasks.

The authors demonstrate that their method significantly outperforms task-specific architectures across 9 out of 12 NLP tasks, including natural language inference, question answering, semantic similarity, and text classification. Notable improvements include:

  • 8.9% on commonsense reasoning (Stories Cloze Test)
  • 5.7% on question answering (RACE)
  • 1.5% on textual entailment (MultiNLI)

This approach minimizes task-specific architecture modifications by using “task-aware input transformations,” which convert structured inputs into a sequence format compatible with the pre-trained model.

This paper laid important groundwork for later transformer-based language models, demonstrating that generative pre-training on unlabeled data could significantly improve performance on downstream language understanding tasks.


GPT-1 was the moment when everything clicked. While ULMFiT showed that transfer learning could work in NLP and BERT demonstrated the power of bidirectional representations, GPT-1 proved that a simple, scalable approach just predicting the next word could create surprisingly capable language models. This paper didn’t just introduce a new model, it established the blueprint that lead to GPT-2, GPT-3, and the entire generative AI revolution.

Problem

The ability to learn effectively from raw text is crucial to alleviating the dependence on supervised learning in natural language processing (NLP). Most deep learning methods require substantial amounts of manually labeled data, which restricts their applicability in many domains that suffer from a dearth of annotated resources

Solution

In this paper, we explore a semi-supervised approach for language understanding tasks using a combination of unsupervised pre-training and supervised fine-tuning. Our goal is to learn a universal representation that transfers with little adaptation to a wide range of tasks. We assume access to a large corpus of unlabeled text and several datasets with manually annotated training examples (target tasks). Our setup does not require these target tasks to be in the same domain as the unlabeled corpus. We employ a two-stage training procedure. First, we use a Language Modeling objective on the unlabeled data to learn the initial parameters of a neural network model. Subsequently, we adapt these parameters to a target task using the corresponding supervised objective.

This was the beginning of the era we live in now. As funny as it may sound, I do not have a lot to add in this section. Because we have already talked about the majority things, the architecture and important concepts like attention in our transformers blog and the training method in our ULMFit section.

So let’s use this section, to talk about the terms we popularly associate with LLMs like Top k, Top p, Temperature, Sampling etc.

Also, since I wrote the transformers blog I have gained a deeper and better understanding of self-attention and masked attention, so we will spend a bit of time on that too.

I will be skipping most of the thing we have already talked about, but if you still wish to get a quick recap of everything you have learned so far about Language models. Consider reading this fabulous blog by Jay Alammar. (you may say that this blog is on gpt-2 and not gpt-1. Well truth be told there is not much difference in gpt, gpt-2 and gpt-3 beside their obvious scale.)

GPT ASAP

Generative Pre-trained Transformer is a decoder only auto-regressive model which was first pre-trained on a humongous amount of data using a Language Modeling method then fine-tuned on a much smaller supervised dataset to help solve specific tasks

That is a lot of ML jargon way of saying that, the authors took the transformer, got rid of the encoder, put up a lot of layers of decoder, trained it on lots of data, then fine tuned it for specific use cases.

Langaguage modeling is pretty straight forward, given a context, predict the next word. The amazing part is that it is unsupervised. We can create a dataset using any sentence/document/text data. We break it down to it’s individual tokens, then we create a dataset by shifting the tokens by 1.

Image of SentencePiece abstract

Model Specification

I took this excerpt directly from the paper as I cannot add anything else to it.

Model specifications Our model largely follows the original transformer work [62]. We trained a 12-layer decoder-only transformer with masked self-attention heads (768 dimensional states and 12 attention heads). For the position-wise feed-forward networks, we used 3072 dimensional inner states. We used the Adam optimization scheme [27] with a max learning rate of 2.5e-4. The learning rate was increased linearly from zero over the first 2000 updates and annealed to 0 using a cosine schedule. We train for 100 epochs on minibatches of 64 randomly sampled, contiguous sequences of 512 tokens. Since layernorm [2] is used extensively throughout the model, a simple weight initialization of N(0, 0.02) was sufficient. We used a bytepair encoding (BPE) vocabulary with 40,000 merges [53] and residual, embedding, and attention dropouts with a rate of 0.1 for regularization. We also employed a modified version of L2 regularization proposed in [37], with w = 0.01 on all non bias or gain weights. For the activation function, we used the Gaussian Error Linear Unit (GELU) [18]. We used learned position embeddings instead of the sinusoidal version proposed in the original work. We use the ftfy library2 to clean the raw text in BooksCorpus, standardize some punctuation and whitespace, and use the spaCy tokenizer.

Why does attention work

I am almost giddy writing this section because I find it astounding that this question never came to my mind. Why does attention even work, we all know it works. But why?

Even before I begin I NEED to mention all these amazing blogs that helped me build an intuition behind the idea

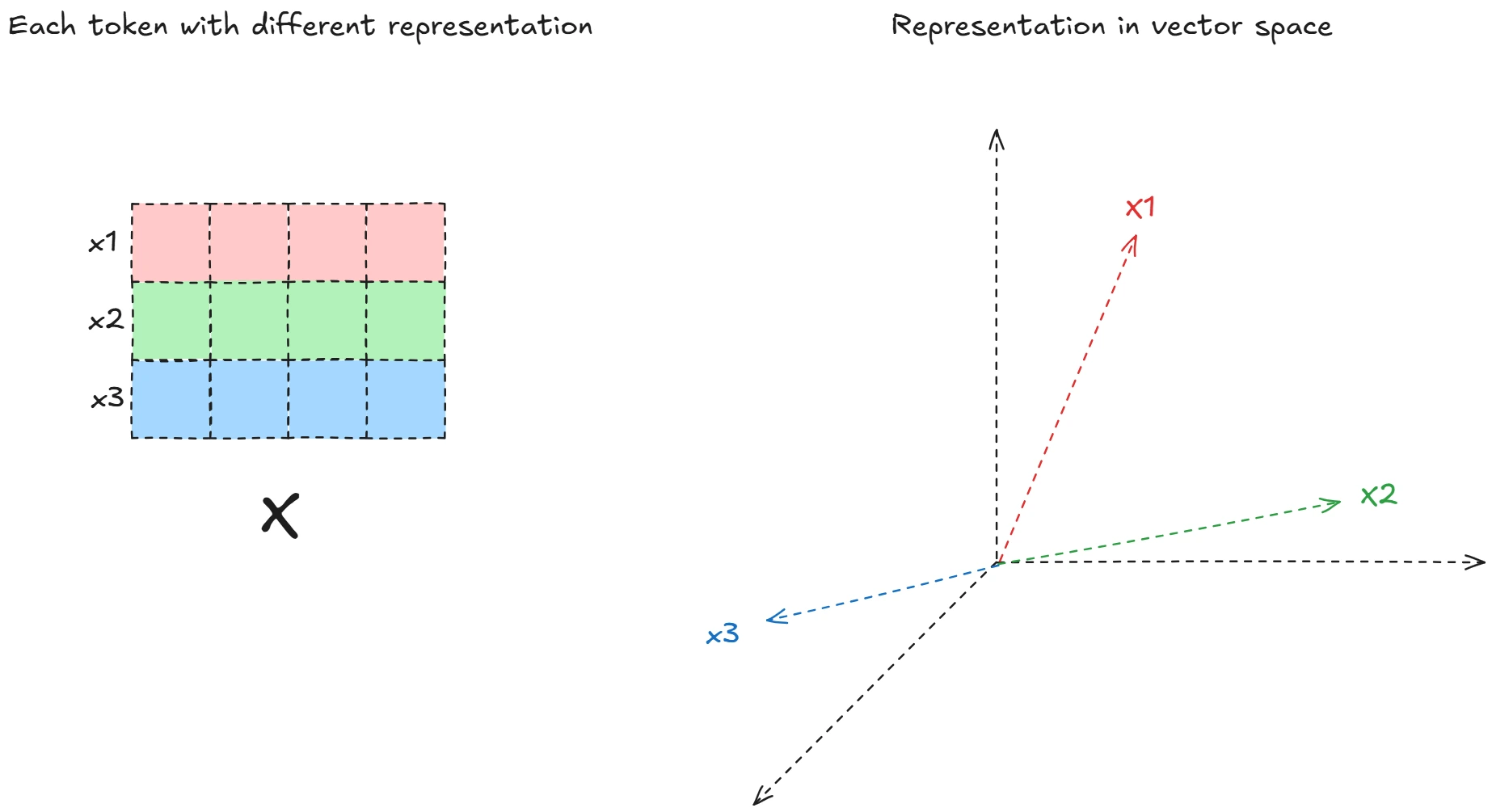
Image of SentencePiece abstract

Let’s forget about Q,K,V for a moment and just focus on a single matrix X. Which contains different tokens (these tokens can be anything. Words, image patches, audio segments, anything that can be embedded and represented by numbers)

This matrix consists of vectors X1, X2, X2…. Xn That make up the matrix X

(X vectors are embedded so they occupy a specific place in space)

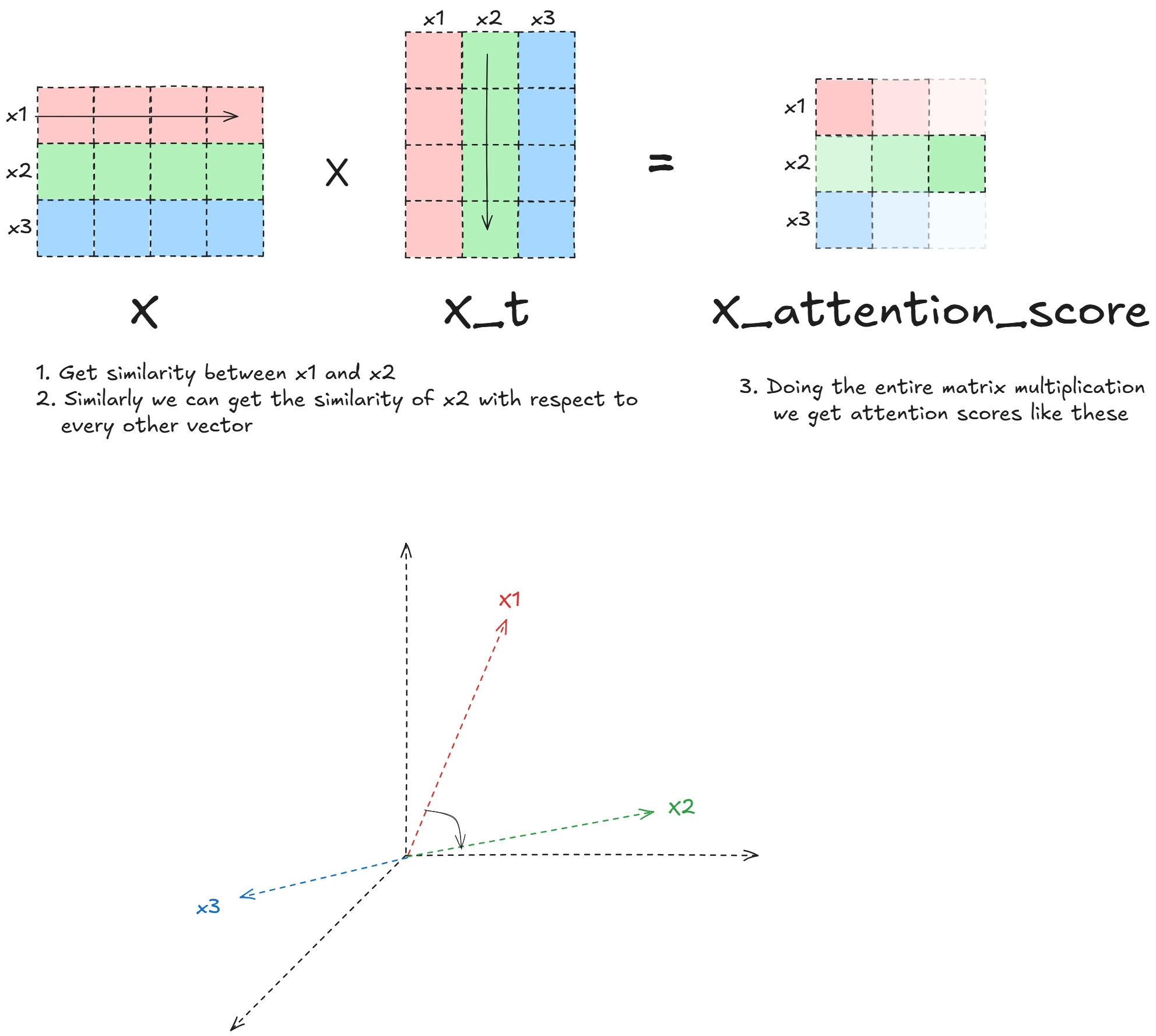
Image of SentencePiece abstract

Now assume you want to see how close X1 is relative to every other word. What do you do? Take dot product, which gives us similarity scores between vectors - the higher the dot product, the more similar (or ‘closer’) the vectors are in the semantic space.

Now let’s say you want to see, how different vectors relate to X1, I.e How far is X2 from X1 (notice how we went from how far X1 is from X2, X3 and so on. To how far X2 is from X1).

Both of the above dot products will give us the same result. I.E how far each vector is relative to each other. This is ATTENTION. Distance between different words. We can think of like this.

In a sentence, “Steve is an amazing person, who loves Machine Learning”. After applying attention, a lot of words will basically get filtered out because we are not paying attention to them anymore

So the sentence becomes

“Steve … amazing …. Machine learning”

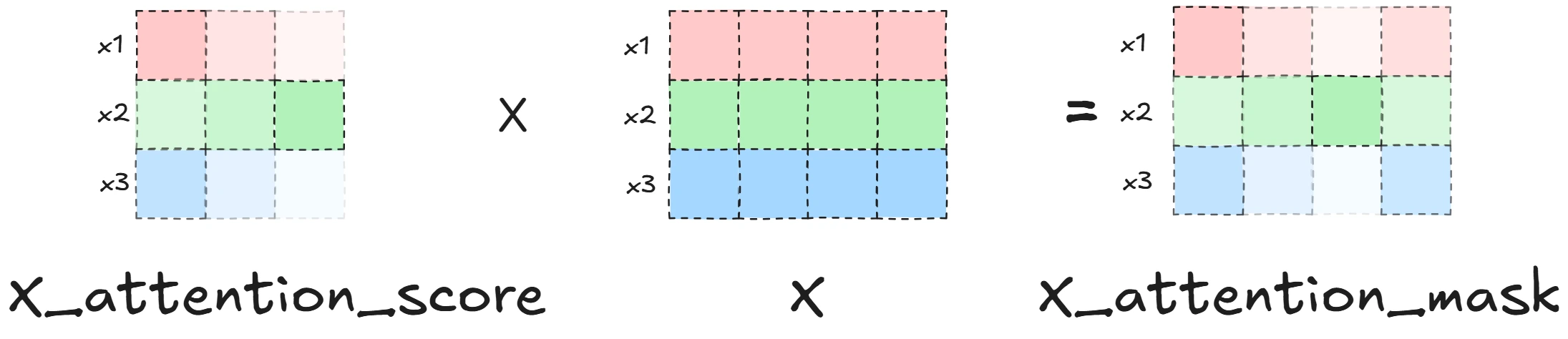
Image of SentencePiece abstract

Now we need to apply these masks to something right, Hence we need to know the original sentence as well

So we multiply this mask with X. This gives us an attention mask over the original matrix.

We just calculated Self-attention. With 1 sentence. Without using the terms Q,K,V.

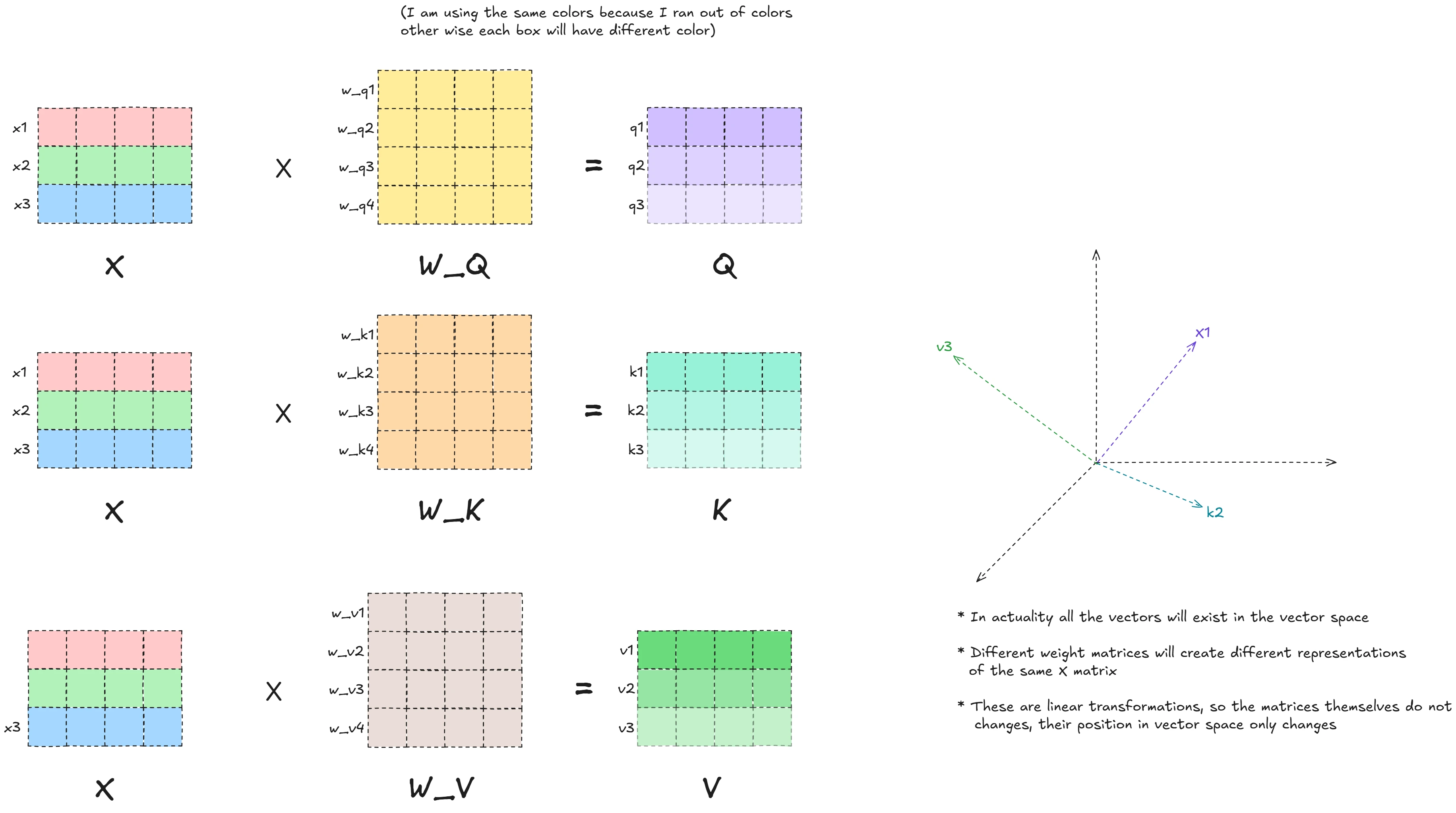
Image of SentencePiece abstract

Now the question arises of W_q, W_k, W_v.

These are linear transformations, they are present to change the position of our X in the vector space.

But dot product gives us the similarity between different vectors in space, by changing representations. We are getting the similarity score from different angles.

This proves that attention works, because dot product is just giving us the similarity in space. What about “but which layer gives us what”

Think of it this way, lets assume our W matrices are all identity matrix. (so no transformation), Now when we do our attention scoring. If any token is more close to any other token it will get a very high score. This essentially gives us the attention of that pair. This will be represented in the first layer, the second layer will then calculate the attention of pairs (much like how CNNs work and are visualized. You start with small lines, then move on to more complex geometric figures)

Now by changing our W matrices in all different ways, we get different representation. And make pairs of different tokens stronger.

Masked Attention

Masked Attention is much like attention itself, but here we get rid of the bi-directional nature. The current token can only look at itself and the tokens before it.

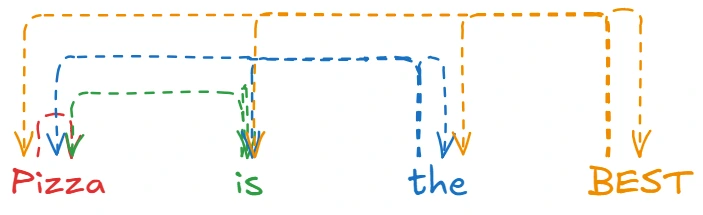
Image of Word2Vec explanation

In a matrix representation is looks something like this, It is very vital. Because our inference is auto-regressive so if during training we can look at the future tokens we run into data leakage, the model would essentially be “cheating” by seeing the answer during training, making it unable to generate text properly during inference when it only has access to previous tokens.

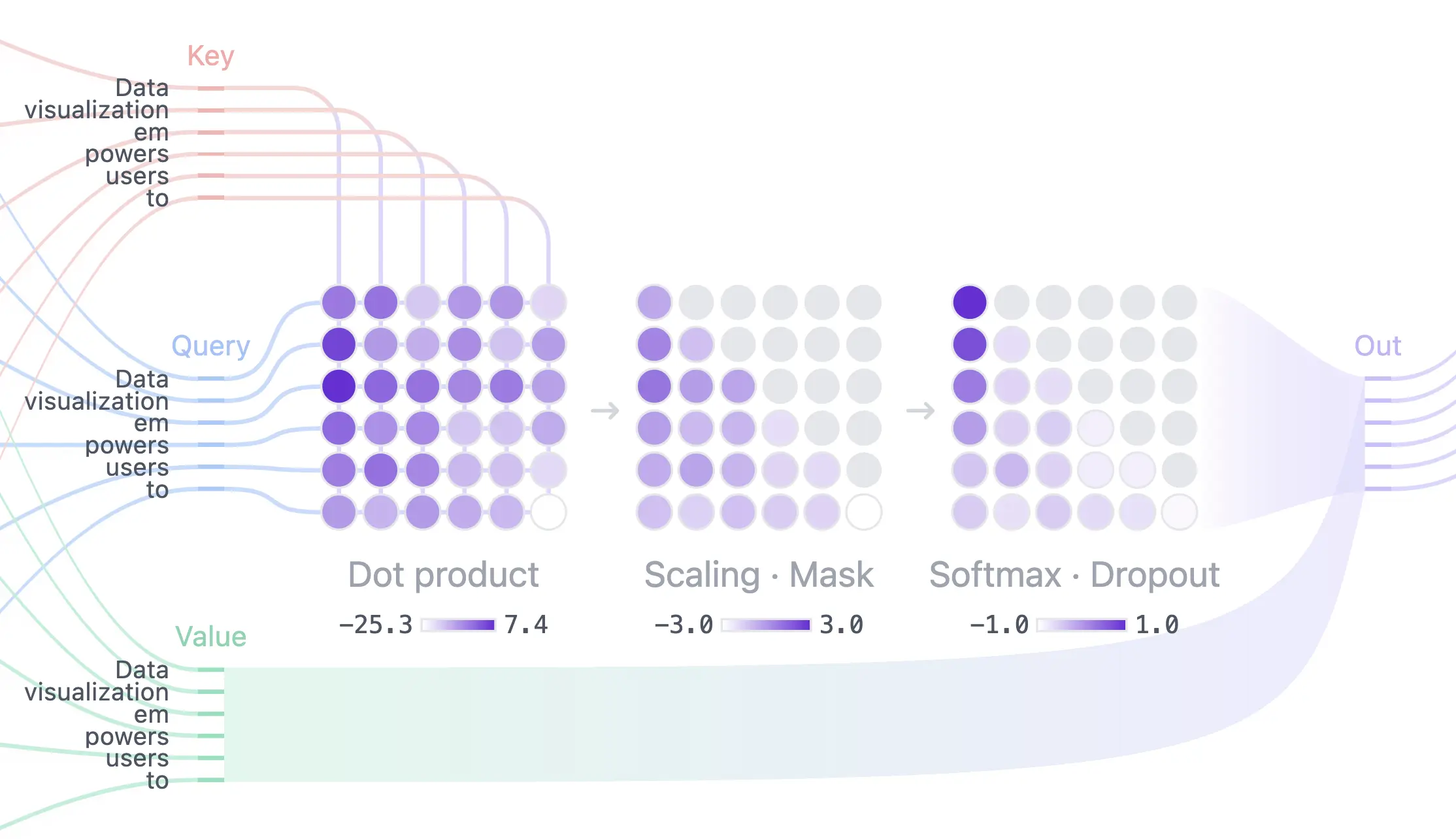Image of SentencePiece abstract Image taken from this beautiful visualizer

The image shows how masked attention works in practice. First we calculate the attention score by multiplying Q and K, then a mask is applied to it. Each token (represented by the colored circles) can only attend to itself and the tokens that came before it. The connections show which tokens each position can “see”, notice how the connections always flow backwards or stay at the same position, never forward. This creates the triangular pattern you see in attention matrices, ensuring the model learns to predict based only on past context.

LLM Glossary

What this is -> A mathematical foundation for terms commonly used during LLM inference
What this is not -> A guide to deciding the best values for your use case

Temperature

\[P(token_i) = \frac{e^{logit_i/T}}{\sum_j e^{logit_j/T}}\]

where T is temperature.

Temperature controls the randomness of token selection by scaling the logits before applying softmax. When T=1, we get the original distribution. As T approaches 0, the model becomes deterministic (always picks the highest probability token). Higher T values (>1) flatten the distribution, making the model more creative but potentially less coherent.

For example if Temperatur is 0, we will always get the same response from the model no matter how many times we run it, for Temperature = 1 we will get varied results.

Top K

\[P_{new}(token_i) = \frac{p_i}{\sum_{j=1}^k p_j}\]

for $i \leq k$, and 0 otherwise

Top-k sampling restricts token selection to only the k most probable tokens, setting all other probabilities to zero before renormalization. If the original probabilities are $[p_1, p_2, …, p_n]$ sorted in descending order, top-k keeps only $[p_1, p_2, …, p_k]$ and renormalizes the tokens using the above formula. This prevents the model from selecting very unlikely tokens while maintaining some randomness.

For example,if the model earlier had 10 most likely options to choose from, by setting Top k=3 we are liminting those options to only 3 most likely options.

Top P (Nucleus Sampling)

\[\sum_{i=1}^k p_i \geq p\]

Top-p sampling dynamically selects the smallest set of tokens whose cumulative probability exceeds threshold p. Given sorted probabilities $[p_1, p_2, …, p_n]$, we find the smallest k such that helps us clear the above criteria, then renormalize only these k tokens. Unlike top-k which uses a fixed number of tokens, top-p adapts to the confidence of the model - using fewer tokens when the model is confident and more when uncertain.

for example, if the model is fairly certain we will have the top token probabilities like [70%, 20%, 4%, 1% …] and if we set top p threshold as 93% we will make the model choose from the top 3 tokens only But if the model is uncertain and we get probabilities like [30%,29%,7%,5%,3%…] the model will have many tokens to choose from.

Sampling Methods

Sampling methods introduce controlled randomness by selecting tokens according to their probability distribution, often producing more diverse and human-like text at the cost of potential coherence.

\[token = \arg\max_i P(token_i)\]

Greedy sampling always selects the token with highest probability. While deterministic and fast, this can lead to repetitive text and suboptimal sequences due to the exposure bias problem.

\[score(sequence) = \frac{1}{|sequence|^\alpha} \sum_{i=1}^{|sequence|} \log P(token_i|context_i)\]

Where α is a length penalty to prevent bias toward shorter sequences.

Beam search maintains multiple candidate sequences simultaneously and explores the most promising ones. Instead of greedily picking the best token at each step, it keeps track of the top k sequences (beams) and expands each one.

Random sampling selects tokens according to their probability distribution without any constraints. While this can produce creative outputs, it often leads to incoherent text as low-probability tokens get selected too frequently.

Consider checking out the transformers documentation by HF.

Repetition Penalty

Repetition penalty reduces the probability of tokens that have already appeared in the generated sequence. The modified logit for a token that appeared n times is:

\[logit_{new} = \frac{logit_{original}}{penalty^n}\]

if penalty > 1, which decreases the likelihood of selecting repeated tokens. This helps prevent the model from getting stuck in repetitive loops while maintaining natural language flow.

Frequency Penalty

Similar to repetition penalty but applies a linear reduction based on token frequency

\[logit_{new} = logit_{original} - \alpha \times count(token)\]

where α is the penalty coefficient and count(token) is how many times the token appeared. This provides more nuanced control over repetition compared to the exponential scaling of repetition penalty.

Presence Penalty

A binary version of frequency penalty that applies a fixed penalty regardless of how many times a token appeared

\[logit_{new} = logit_{original} - \alpha\]

if the token was seen before, unchanged otherwise. This encourages the model to use new vocabulary without heavily penalizing natural repetitions that occur in coherent text.

That wraps up our section on GPT, don’t worry as we move forward to the future years we will talk about how LLMs work with RL, How different architectures affect different things, talk about optimizers and so much more. For now I feel like these are the most we should keep for this year.

Sentencepiece

Image of SentencePiece abstract

Link to the paper: SentencePiece: A simple and language independent subword tokenizer and detokenizer for Neural Text Processing

Quick Summary

This paper introduces SentencePiece, an open-source subword tokenizer and detokenizer designed specifically for neural text processing, including Neural Machine Translation (NMT). The key innovation of SentencePiece is that it can train subword models directly from raw sentences without requiring pre-tokenization, enabling truly end-to-end and language-independent text processing.

The authors highlight several important features:

  1. It implements two subword segmentation algorithms: byte-pair encoding (BPE) and unigram language model
  2. It provides lossless tokenization that preserves all information needed to reconstruct the original text
  3. The model is fully self-contained, ensuring reproducibility across implementations
  4. It offers efficient training and segmentation algorithms
  5. It includes library APIs for on-the-fly processing

They validate their approach through experiments on English-Japanese translation, showing comparable accuracy to systems that use pre-tokenization, while being significantly faster for non-segmented languages like Japanese.


Tokenization might seem like a boring preprocessing step, but it’s actually one of the most crucial components of any language model. Think of it as teaching a computer how to “read” - before a model can understand Shakespeare or debug your code, it needs to know how to break text into meaningful chunks. SentencePiece was a game-changer because it made this process truly language-agnostic.

Problem

Tough to make NMT language independent

Before SentencePiece, building multilingual NLP systems was a nightmare. Each language needed its own custom preprocessing pipeline - Japanese needed special word segmentation, Chinese required different tokenization rules, and languages like Thai had their own complexities. This meant you couldn’t easily train one model across multiple languages, severely limiting the scope and efficiency of NLP systems.

Solution

SentencePiece comprises four main components: Normalizer, Trainer, Encoder, and Decoder. Normalizer is a module to normalize semantically equivalent Unicode characters into canonical forms. Trainer trains the subword segmentation model from the normalized corpus. We specify a type of subword model as the parameter of Trainer. Encoder internally executes Normalizer to normalize the input text and tokenizes it into a subword sequence with the subword model trained by Trainer. Decoder converts the subword sequence into the normalized tex

The following articles helped me write this section

What are tokenizers?

As we have discussed earlier. Machines do not understand words, They understand numbers. Tokens are basically words represented as numbers that Language Models use to communicate. (You will see why this is an oversimplification in a minute?)

Why call them tokens if they are just words?

Taking back what I said, they aren’t exactly words. Let us understand why.

Word Level Tokenization

Let’s start with a simple sentence and tokenize (converting words in a document to token) it.

Example: “I love machine learning”
Tokens: [“I”, “love”, “machine”, “learning”]
Token IDs: [1, 234, 5678, 9012]

Now imagine instead of a sentence, it was a page, or a whole book. It will contain thousands if not hundreds of thousands of unique words. There are languages which have more than a million unique words. It will be unfeasible to tokenize each word.

Also what if we run into a word we have never seen during training. That will break our model, to overcome this, we can use something called Character Level Tokenization.

Character Level Tokenization

Let’s again start with the same sentence

Example: “I love machine learning”
Tokens: [“I”, “ “, “l”, “o”, “v”, “e”, “ “, “m”, “a”, “c”, “h”, “i”, “n”, “e”, “ “, “l”, “e”, “a”, “r”, “n”, “i”, “n”, “g”]
Token IDs: [1, 2, 12, 15, 22, 5, 2, 13, 1, 3, 8, 9, 14, 5, 2, 12, 5, 1, 18, 14, 9, 14, 7]

This fixes our problem of a huge vocabulary, but we run into another issue. Characters by themselves do not hold any meaning. This removes any semantic relation.

Image of SentencePiece abstract(Unless it’s E ofc)

There have been innovations made to fix these problems, let’s look into them one by one.

Subword Tokenization

The idea is quite simple, In our previous word level tokenization. Fun, Funny, Funniest ,and other variations of the word Fun will be treated as different tokens. So in sub-word tokenization. We break down the words, something like Fun + niest.

The reason being in english we add a lot of different pre-fixes (Like un to funny that makes it unfunny) and suffixes (Like niest to Fun to get Funniest). The techniques of forming these subwords varies from different techniques to different techniques. Let’s explore them

Byte-pair encoding

This blog helped me immensely with this section.

Byte-pair encoding (BPE) was introduced in Neural Machine Translation of Rare Words with Subword Units (Sennrich et al., 2015). This is the encoding method the famous tiktoken tokenizer of OpenAI uses.

It essentially follows two steps, the pretokenization then merging. Let’s understand each.

In the pretokenization step, we determine the set of unique words in the training data along with their frequency. Using this unique set, BPE breaks the words down into it’s individual characters, which are then merged to form the final vocabulary. Let’s understand it with an example.

Suppose after the pre-tokenization step, we have the following words with their frequencies that we got from the training data

("hug", 10), ("pug", 5), ("pun", 12), ("bun", 4), ("hugs", 5)

Consequently, the base vocabulary is ["b", "g", "h", "n", "p", "s", "u"]. Splitting all words into characters of the base vocabulary, we get:

("h" "u" "g", 10), ("p" "u" "g", 5), ("p" "u" "n", 12), ("b" "u" "n", 4), ("h" "u" "g" "s", 5)

BPE then counts the character pair with the high frequencies and then pairs them up. Like here it will first pair up u and g as they occur the most together (10 times in hug, 5 times in pug and 5 more times in hugs. Totalling 20 times). This pair ug is then added to the vocabulary.

("h" "ug", 10), ("p" "ug", 5), ("p" "u" "n", 12), ("b" "u" "n", 4), ("h" "ug" "s", 5)

Then we identify the next most frequent pair, that will be u and n that occur 16 times together. Then the next most frequent pair interestingly is h with ug which occur together 15 times. (This teaches an important lesson, we do not only consider characters or symbols while pairing them up. But the frequency pairs that exist in the vocabulary).

Now our entire vocabulary looks something like this ["b", "g", "h", "n", "p", "s", "u", "ug", "un", "hug"] and our set of unique words

("hug", 10), ("p" "ug", 5), ("p" "un", 12), ("b" "un", 4), ("hug" "s", 5)

Assuming we stop our merging at this point. Our new vocabulary will be used to tokenize new words (Unless they were not present in our training data). For example, "bug" will be tokenized to ["b", "ug"] but “mug” would be tokenized as ["<unk>", "ug"] since the symbol "m" is not in the base vocabulary.

In general, single letters such as “m” are not replaced by the “" symbol because the training data usually includes at least one occurrence of each letter, but it is likely to happen for very special characters like emojis.

Using BPE the vocab size is the base vocabulary size + the number of merges, which is a hyperparameter we can choose. For instance GPT has a vocabulary size of 40,478 since they have 478 base characters and chose to stop training after 40,000 merges.

Wordpiece

Wordpiece is very similar to our BPE algorithm. It starts with the same idea of pre-tokenization followed by merging. It differs in the way it merges - instead of following the highest frequency, it merges based on a scoring system that considers how valuable each merge is.

The key difference is in how pairs are selected for merging:

WordPiece doesn’t just pick the most frequent pair like BPE does. Instead, it calculates a score for each pair by dividing how often the pair appears together by how often each part appears separately. This means it prefers to merge pairs where the individual parts are rare on their own, but common when together. This approach ensures that merges actually improve the tokenization rather than just combining frequent but unrelated pieces.

\[score = \frac{freq\_of\_pair}{freq\_of\_first\_element \times freq\_of\_second\_element}\]

HF also has a short course on LLMs where they talk about wordpiece pretty well.

Taking an excerpt from the said course explains it well

By dividing the frequency of the pair by the product of the frequencies of each of its parts, the algorithm prioritizes the merging of pairs where the individual parts are less frequent in the vocabulary. For instance, it won’t necessarily merge (“un”, “##able”) even if that pair occurs very frequently in the vocabulary, because the two pairs “un” and “##able” will likely each appear in a lot of other words and have a high frequency. In contrast, a pair like (“hu”, “##gging”) will probably be merged faster (assuming the word “hugging” appears often in the vocabulary) since “hu” and “##gging” are likely to be less frequent individually.

If you are interested, I will recommend reading this blog by google which talks about Wordpiece more in depth.

Unigram

The same course talks about Unigram as well.

Unigram is quite different from our previously discussed tokenization methods like BPE and WordPiece. Instead of expanding the vocabulary, it starts with a big vocabulary and gradually trims down irrelevant tokens.

At each step of training, the Unigram model computes the loss over the entire corpus. Then, for each token it calculates how much the loss will increase if the token is removed, and removes the ones which increase the loss the least.

Note that we never remove the base characters, to make sure any word can be tokenized.

Using the same example as above we start with a sample corpus

("hug", 10), ("pug", 5), ("pun", 12), ("bun", 4), ("hugs", 5)

We calculate the frequencies of all the subwords as below

("h", 15) ("u", 36) ("g", 20) ("hu", 15) ("ug", 20) ("p", 17) ("pu", 17) ("n", 16)
("un", 16) ("b", 4) ("bu", 4) ("s", 5) ("hug", 15) ("gs", 5) ("ugs", 5)

To tokenize a given word, we look at all possible subwords and calculate their probabilities. All the tokens are considered independent of each other so we can just multiply all sub-tokens as below

For the word hug, by tokenizing it as h,u, and g

\(P(h) \times P(u) \times P(g)\) \(\frac{15}{210} \times \frac{36}{210} \times \frac{20}{210} = 0.000389\)

It is also tokenized as hu, g and h, ug, and hug. The scores are

["h", "u", "g"] = 0.000389
["hu", "g"] = (15/210) × (20/210) = 0.0095
["h", "ug"] = (15/210) × (20/210) = 0.0095
["hug"] = 15/210 = 0.071

Hence hug will be tokenized as [“hug”] as it has the highest probability.

In practice this iterative process is not used, but rather Viterbi algorithm is used to find the subword tokenization with the maximum probability.

Using this same method a score is calculated for all the words, as below

"hug": ["hug"] (score 0.071428)
"pug": ["pu", "g"] (score 0.007710)
"pun": ["pu", "n"] (score 0.006168)
"bun": ["bu", "n"] (score 0.001451)
"hugs": ["hug", "s"] (score 0.001701)

We want to calculate the negative log likelihood of the whole corpus and that becomes

freq("hug") × (-log(P("hug"))) + freq("pug") × (-log(P("pug"))) + freq("pun") × (-log(P("pun"))) + freq("bun") × (-log(P("bun"))) + freq("hugs") × (-log(P("hugs")))
10 × (-log(0.071428)) + 5 × (-log(0.007710)) + 12 × (-log(0.006168)) + 4 × (-log(0.001451)) + 5 × (-log(0.001701)) = 169.8

Now each token is removed to see how that affects the overall loss as below

Removing token “pu”: Loss change = 0 (since “pug” can use [“p”, “ug”] with same score) Removing token “hug”: Loss increases by 23.5 (forces less optimal tokenizations)

Tokens with the smallest loss increase are removed first until the desired vocabulary size is reached.

SentencePiece

This is a fabulous blog on the topic, it explains everything along with the implementation code. Consider checking it out.

This sub-section will be the shortest even though this section is about sentencepiece, you know why? well because sentencepiece is not a tokenizer at all, it’s a pre-tokenization algorithm used in conjunction with unigram or BPE.

All tokenization methods talked about so far have the same problem, they assume that the input text uses spaces to separate words. However, not all languages use spaces to separate words. One possible solution is to use language specific pre-tokenizers, e.g. XLM uses a specific Chinese, Japanese, and Thai pre-tokenizer. To solve this problem more generally, SentencePiece treats the input as a raw input stream, thus including the space in the set of characters to use. It then uses the BPE or unigram algorithm to construct the appropriate vocabulary.

Decoding with SentencePiece is very easy since all tokens can just be concatenated and “▁” is replaced by a space.

All transformers models in the library that use SentencePiece use it in combination with unigram. Examples of models using SentencePiece are ALBERT, XLNet, LLama2, etc.

Well that is all there is to know about SentencePiece really, if you want to know how it is implemented you can check out the blog I mentioned above.

BERT

Image of BERT

Link to paper: BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding

Quick Summary

This paper introduces BERT (Bidirectional Encoder Representations from Transformers), a groundbreaking language representation model that significantly advanced the state of natural language processing in 2018. The key innovation of BERT is its ability to pre-train deep bidirectional representations from unlabeled text, unlike previous models that were limited to unidirectional contexts (either left-to-right or right-to-left).

BERT employs two novel pre-training tasks:

  1. Masked Language Model (MLM): Randomly masks some percentage of input tokens and predicts those masked tokens
  2. Next Sentence Prediction (NSP): Predicts whether two sentences follow each other in original text

These pre-training objectives allow BERT to create context-aware representations that capture information from both left and right contexts. After pre-training on large text corpora (BookCorpus and Wikipedia), BERT can be fine-tuned with just one additional output layer to create state-of-the-art models for a wide range of NLP tasks without task-specific architecture modifications.

The paper demonstrated significant improvements over previous methods on eleven NLP tasks, including the GLUE benchmark, SQuAD, and SWAG datasets.


These two blogs helped me immensely with this section:

This paper wasn’t trying to find a problem then solve it per se. It is more of an innovation, taking an excerpt from the paper.

BERT is designed to pretrain deep bidirectional representations from unlabeled text by jointly conditioning on both left and right context in all layers. As a result, the pre-trained BERT model can be finetuned with just one additional output layer to create state-of-the-art models for a wide range of tasks, such as question answering and language inference

Problem

Previous language models like GPT-1 and ELMo had a fundamental limitation: they could only look in one direction. GPT-1 used masked attention (only seeing previous tokens), while ELMo concatenated separate left-to-right and right-to-left models. But human language understanding is inherently bidirectional - to understand “The animal didn’t cross the street because it was too [tired/wide],” you need context from both sides to know whether “it” refers to the animal or the street.

Solution

BERT solved this by using the encoder portion of the Transformer architecture, which allows true bidirectional attention. Instead of predicting the next word (like GPT), BERT learns by predicting masked words using context from both directions simultaneously.

All the papers I have mentioned in this blog are great, but the BERT paper is particularly awesome. It stands out even today, and the sheer amount of innovations from one paper is astounding. I implore you to check it out.

Let’s first answer the question what is BERT?

BERT stands for Bi-directional Encoder Representation from Transformers. That’s a mounthful, the name aside. It is quite simple, Remember our Transformers, Well this is essentially that but only the encoder (Quite the opposite of GPT). Bi-directional means that it looks both ways, forward and backward. Remember in GPT we used masked self-attention which only got representation for current and previous token, well the encoder uses vanilla self-attention which gets representation from both sides. The transformer part is pretty self explanatory.

What is it used for?

This is the most amazing thing about BERT, it can be used for a plethora of NLP tasks like question answering, Parts of speech taging, Sentiment analysis, Classification etc. This is due to the way it is trained.

How is it trained?

Much the way we have discussed before, it has a pre-training phase in which we feed it lots and lots of data for it to learn a representation. Then fine-tune it for the particular task we would like it for.

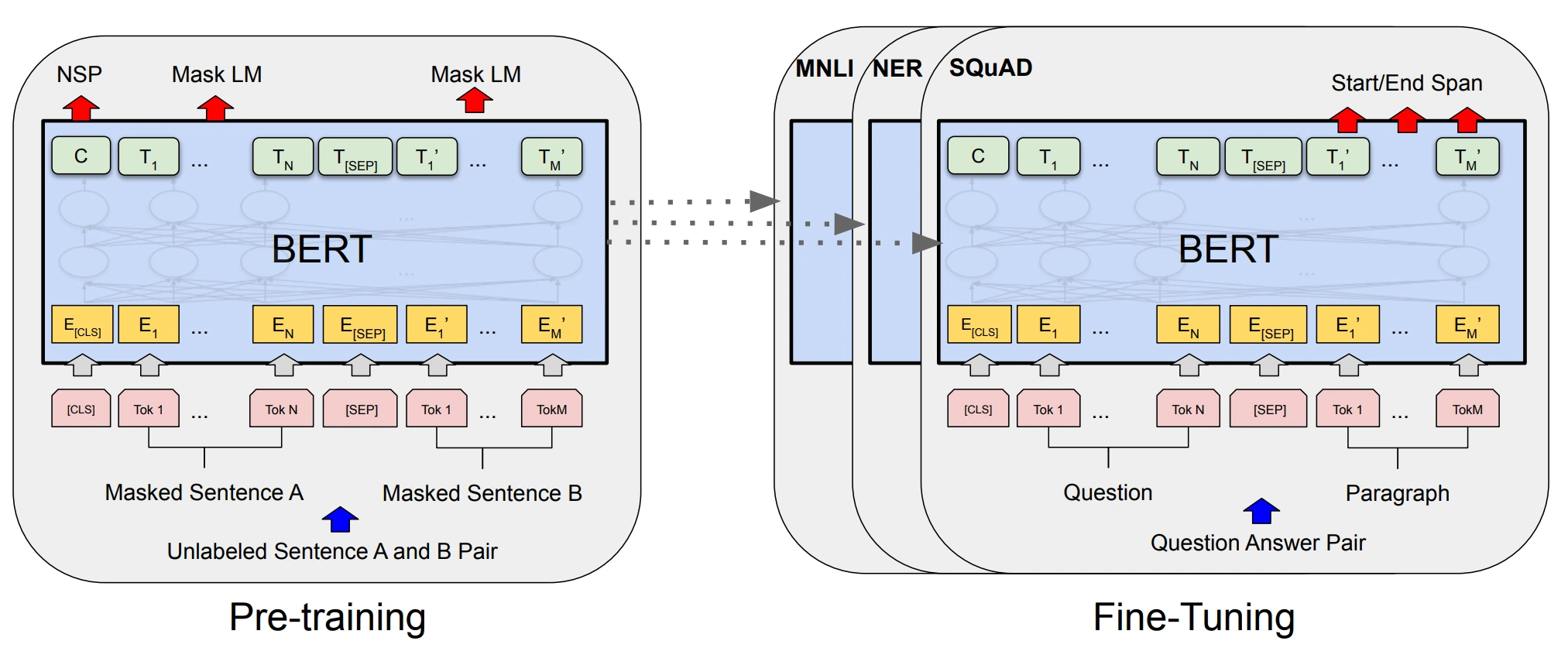Image of BERT Image taken from the paper

There are a lot of new terms from the above image like CLS, Masked LM, NSP etc that may not make sense at first. But they are quite simple once we understand them. Let us begin

Masked Language Modeling

This is one of the methods of pre-training BERT. We take the input sentence and randomly mask out 15% of the tokens, then using the output of the position we try to predict what could have been the possible text.

In practice, 80% of the times the token is masked, 10% of the times it is replaced with a random token and other 10% of the time it’s left unchanged.

Let’s see this in action:

  • Original: “The cat sat on the mat”
  • Masked: “The cat [MASK] on the mat”
  • BERT sees both “The cat” and “on the mat” to predict “sat”

This bidirectional context is why BERT became so powerful for understanding tasks.

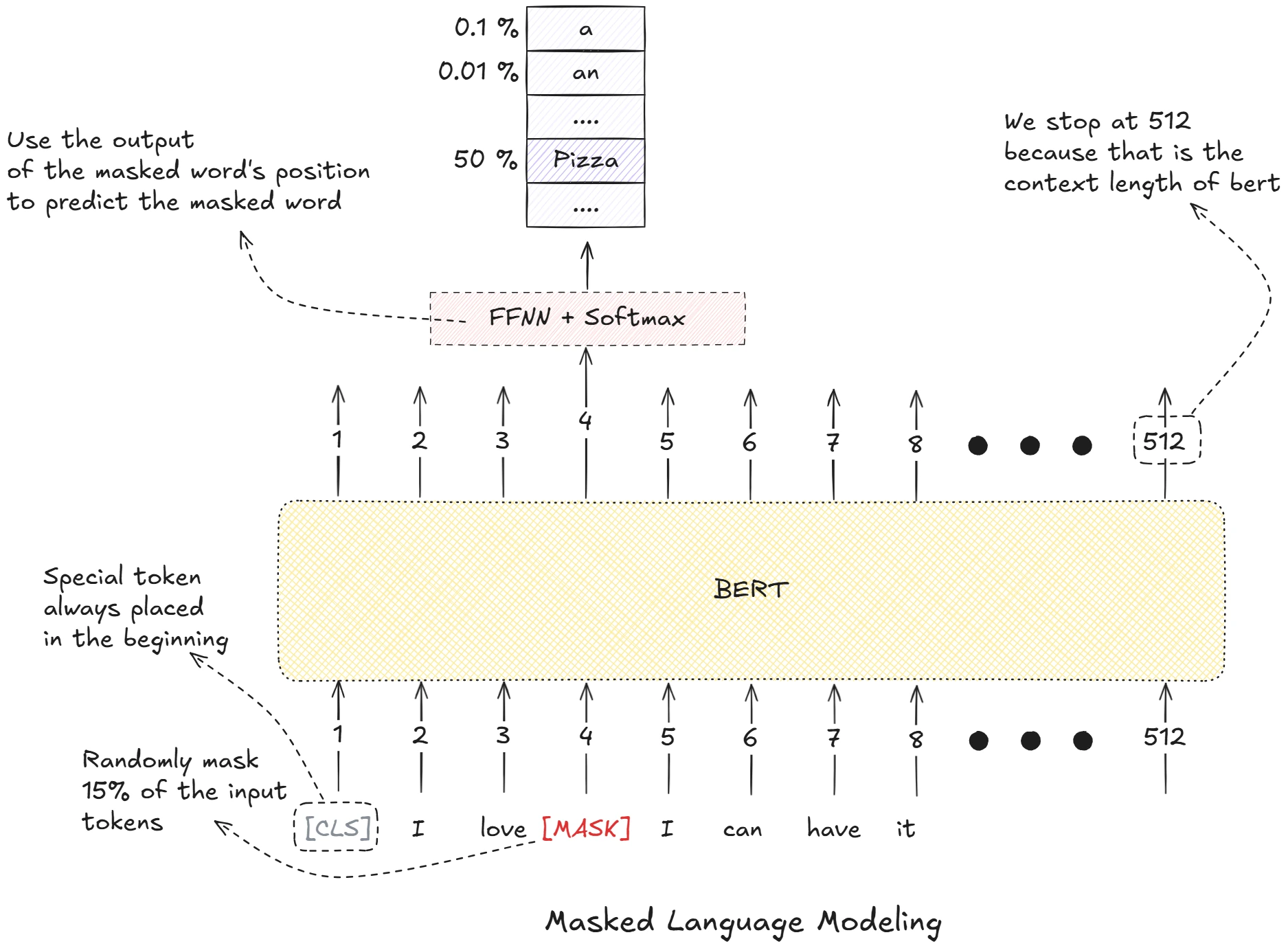
Image of BERT

Next Sentence Prediction

Next Sentence Prediction is exactly what it sounds like, but instead of predicting the next sentence. We predict if the given next sentence will come after the first sentence.

The special token CLS learns representation from the both the sentences and the output from it’s position is used to predict whether the sentence comes next or not. In practice, the CLS token is fine tuned for classification, sentiment analysis etc. SEP is a special token that acts as a seperator between both the sentences.

In reality, both NSP and MLM are done simultaneously.

Image of BERT

Fine-Tuning

The BERT paper is quite accessible, and has great visuals too. The below image is directly taken from it and shows that to fine tune we just use a small set of training data with labels to fine-tune bert for a specific task.

Image of BERT

We can use bert to generate embeddings too!! Much like the way we did with ELMo. How? well I leave that upto you to explore.

Why BERT was Revolutionary

Before BERT, each NLP task needed its own specialized architecture. Question answering systems, sentiment classifiers, and named entity recognizers all looked completely different. BERT changed this by providing a universal representation that could be fine-tuned for any task with just a small additional layer.

And that concludes BERT too, now we have talked about the two big architectures of LLMs, moving forward we will mostly be talking about the innovations done in the architecture and the solutions found to increase the scale at which to train them.

2019: Scaling and Efficiency

GPT-2

Image of GPT-2

Link to paper: Language Models are Unsupervised Multitask Learners,blog

Quick Summary

This 2019 paper by Radford et al. (OpenAI) introduces GPT-2, a large-scale language model that demonstrates impressive zero-shot learning capabilities across multiple NLP tasks. The key insight of this paper is that language models trained on sufficiently large and diverse datasets naturally acquire the ability to perform various language tasks without explicit supervision.

Key contributions:

  1. Introduction of WebText - a high-quality web dataset created by scraping outbound links from Reddit with at least 3 karma
  2. Development of GPT-2, a Transformer-based language model with 1.5 billion parameters
  3. Demonstration that a single unsupervised language model can perform multiple NLP tasks without task-specific training
  4. Evidence that model performance scales in a log-linear fashion with model size

The paper shows that GPT-2 achieves state-of-the-art results on 7 out of 8 tested Language Modeling datasets in a zero-shot setting. It also demonstrates promising zero-shot performance on tasks like reading comprehension, summarization, translation, and question answering without any task-specific fine-tuning.

This work represents a significant step toward building more general NLP systems that can learn to perform tasks from naturally occurring demonstrations in text, rather than requiring task-specific datasets and architectures for each application.


This was paper was an improvement over the original GPT, and a huge scaling of it

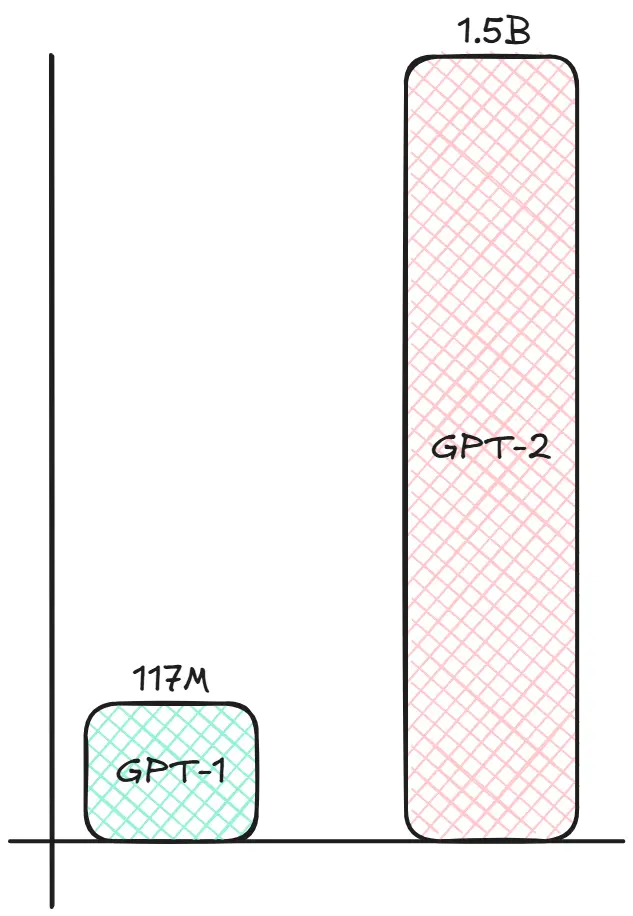
Image of scale difference between gpt-1 and gpt 2

My first question was how did one even get so much data? The authours have underlined that well. So quoting the paper

Common Crawl. Trinh & Le (2018)’s best results were achieved using a small subsample of Common Crawl which included only documents most similar to their target dataset, the Winograd Schema Challenge. While this is a pragmatic approach to improve performance on a specific task, we want to avoid making assumptions about the tasks to be performed ahead of time. Instead, we created a new web scrape which emphasizes document quality. To do this we only scraped web pages which have been curated/filtered by humans. Manually filtering a full web scrape would be exceptionally expensive so as a starting point, we scraped all outbound links from Reddit, a social media platform, which received at least 3 karma. This can be thought of as a heuristic indicator for whether other users found the link interesting, educational, or just funny. The resulting dataset, WebText, contains the text subset of these 45 million links. To extract the text from HTML responses we use a combination of the Dragnet (Peters & Lecocq, 2013) and Newspaper1 content extractors. All results presented in this paper use a preliminary version of WebText which does not include links created after Dec 2017 and which after de-duplication and some heuristic based cleaning contains slightly over 8 million documents for a total of 40 GB of text. We removed all Wikipedia documents from WebText since it is a common data source for other datasets and could complicate analysis due to over…

My second question was how do you run such large models economically?

(Obviously I have skipped how do you “train” such large models, as we will be talking about that in the next section)

And the answer came in the form of …

KV Cache!!!

These two blogs helped me immensely while writing this section, check’em out!!! (they have very nice animations)

Image of quick inference in LLMs

Before we start understanding KV Cache, let us revisit our inference to see what happens.

Let’s say we ask the LLM a question. “Captial of India?” (we already know what happens inside an LLM so I have skipped a lot of the blocks except the essential ones)

Using that, a matrix is formed, for each token id we have embeddings, using which Q,K, and V matrices are made. That gives us our attention values, That is fed to a feed forward network which outputs a vector of logits vocab size, after passing it through softmax let’s say we take the token id with the maximum probability. This gives us a vector output, of token id. (Here I am showing the embeddings)

The embedding of this token is then appended to our original input X, and this operation is repeated till we run into the token (End of sentence token)

Now if we do not cache anything, these values need to be calculated again and again whenever a new token is added as shown above

But we only need to get the attention value for the latest query, we can save the previously calculated queries. (If you are having a hard time thinking why? I will explain it in a while. Hint: Masked Causal attention)

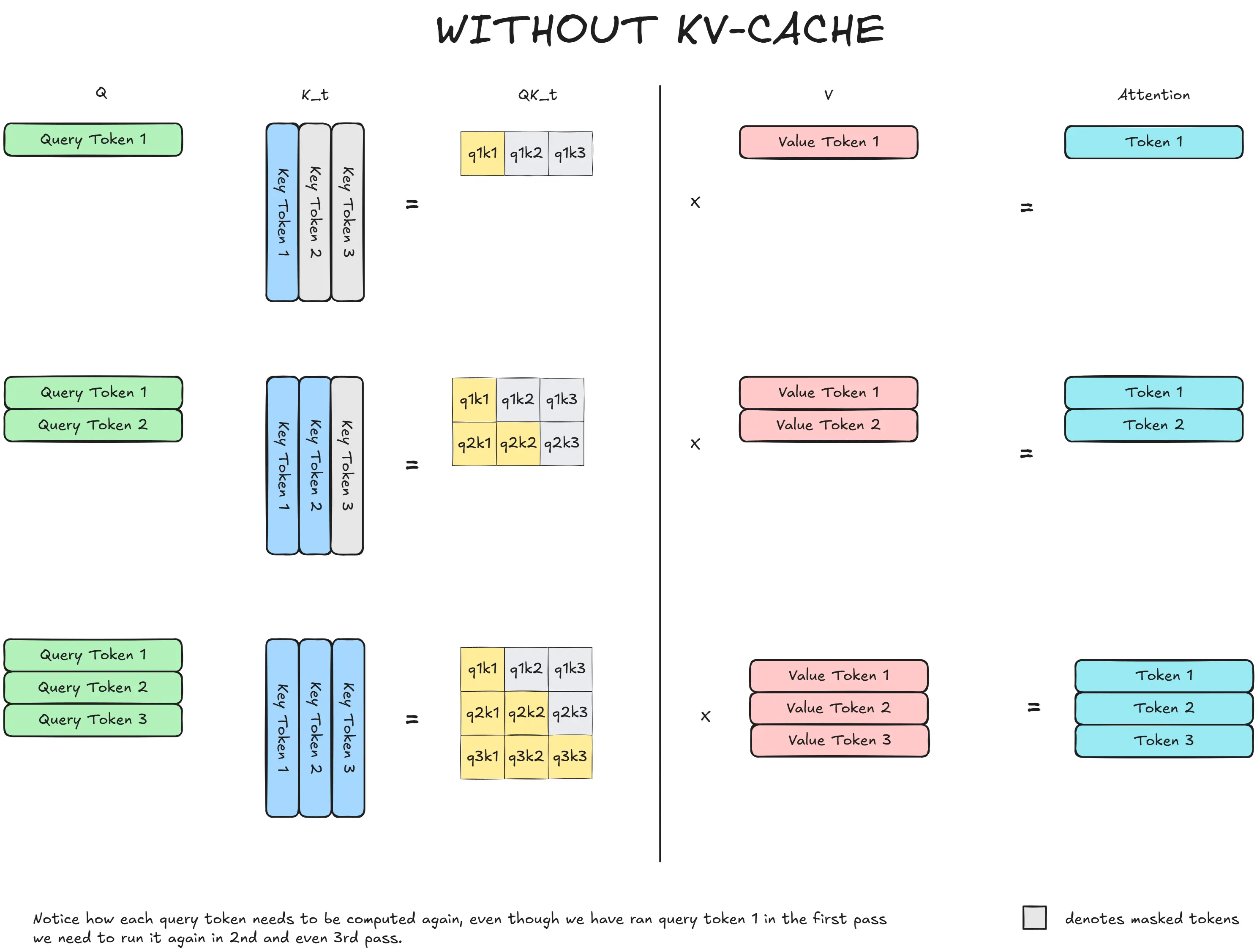
Image of inference without KV cache

Let’s look closer at the attention calculation itself, If we go vector by vector. We can see that we need to compute $QK^t$ again and again, each time a new token is calculated.

But we do not need to do this for a decoder, as previous tokens never attend to the future tokens. We can just cache the attention of previous tokens and compute the attention score for the latest token!

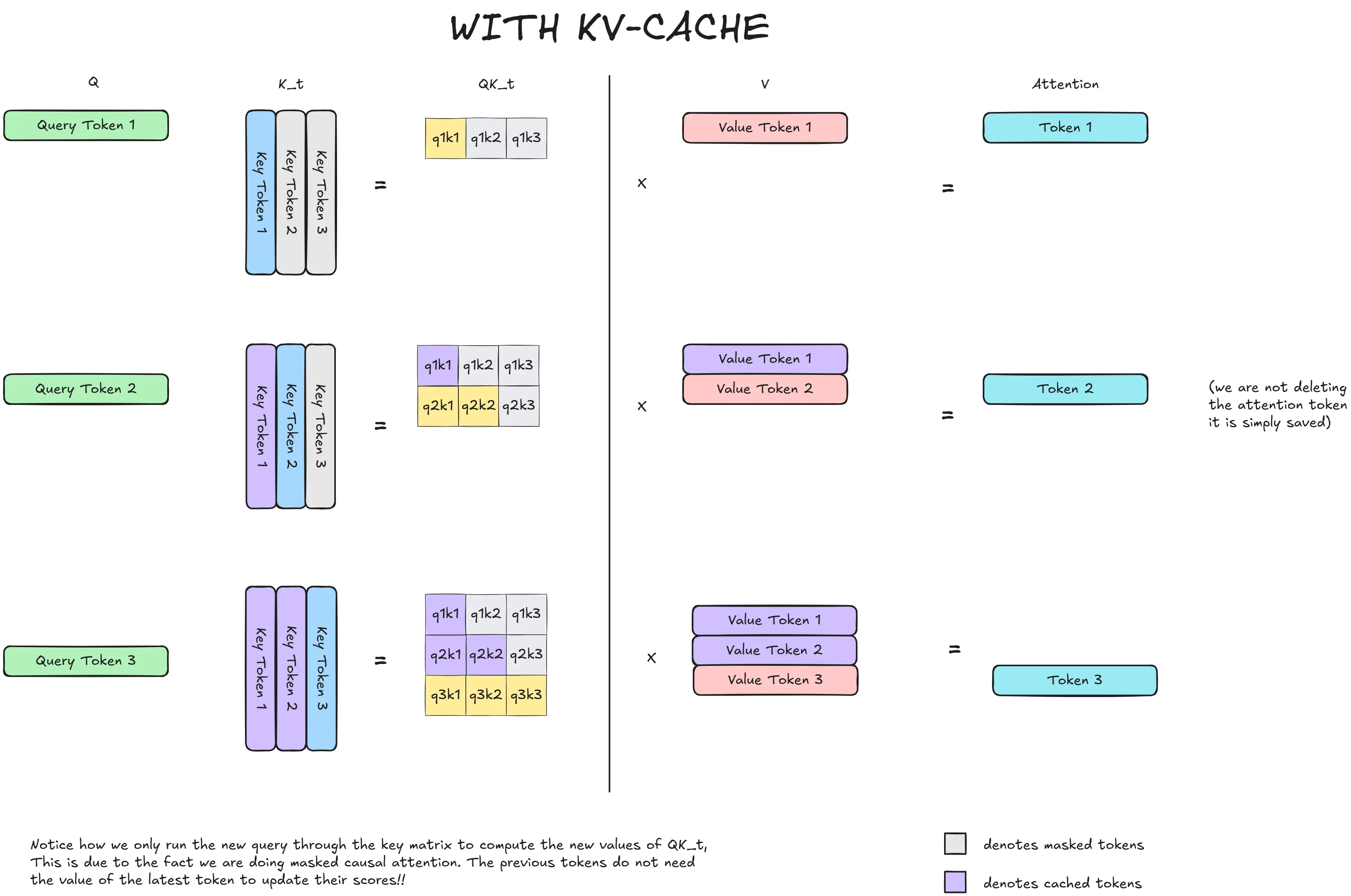
Image of inference with KV cache

I had two interesting discoveries during this:

  • We only cache $K$ and $V$ not $Q$. Because there is no point storing it. To calculate the latest attention score we need the entire $K$ and $V$, but not $Q$. For nth token $Q$, we need the entire of K to calculate $QK^t$. Then we need to multiple the entire $V$ to get the latest attention score. (This is definitely tough to think about, pause take a moment and image it)
  • When we append another vector, the shape of $K$ and $V$ also change. But we do not calculate the values of old $Q$ with these because of our masking (We do not need to see the future values), $Q_1$ has no point being multiplied with $K_4$ as that will be masked as infiti anyhoo (We have already talked about this).

The second point also gives us another amazing point, KV caching is not possible in models like BERT (Think why?)

P.S. KV-Cache was not introduced in gpt-2 but became wildly popular after it. I am not able to find the source of the idea. Comment down below if you know about it!!!

That pretty much covers the amazing things that the GPT-2 paper talked about, Let’s move on to see how we can train such big models.

RoBERTa

Image of RoBERTa

Link to paper: RoBERTa: A Robustly Optimized BERT Pretraining Approach

Quick Summary

This 2019 paper by Liu et al. from Facebook AI presents RoBERTa (Robustly Optimized BERT Pretraining Approach), which demonstrates that BERT was significantly undertrained and can achieve state-of-the-art performance with careful optimization choices.

Key contributions:

  1. The paper identifies several critical design decisions that significantly improve BERT’s performance:

    • Training the model longer with larger batches over more data
    • Removing the Next Sentence Prediction (NSP) objective
    • Training on longer sequences
    • Dynamically changing the masking pattern applied to training data

  2. The researchers collect a larger dataset (including a new CC-NEWS corpus) to better control for training set size effects.

  3. Through extensive experimentation, they show that when properly optimized, BERT’s masked Language Modeling objective is competitive with newer approaches like XLNet.

  4. RoBERTa achieves state-of-the-art results on GLUE, RACE, and SQuAD benchmarks without multi-task fine-tuning for GLUE or additional data for SQuAD.

The authors emphasize that seemingly mundane training decisions (like batch size, training time, and dataset size) can have as much impact on final performance as architectural innovations. This raises important questions about the source of improvements in recent NLP models and highlights the need for careful replication studies.

The paper is particularly notable for its thorough empirical analysis of training hyperparameters and careful ablation studies showing the contribution of each modification to overall performance.


Problem

The authors found that most of the models released post BERT were challenging to train, hard to compare and they were mostly working as a black box and it was difficult to tell which hyper-parameter were significant. RoBERTa was a replication study on BERT to better understand it. And they unearthed that BERT was significantly under trained.

Solution

  1. Present a set of important BERT design and training strategies
  2. Introduction of a novel dataset (CCNEWS)

Dynamic Masking

While training BERT a static masking strategy is employed. I.e the same words are masked throughout training, This can lead to the model memorizing these positions instead of generalizing and learning the relationship between words.

Dynamic masking was a method made to mitigate this issue by varying the masked positions in each epoch. This lead to greater generalization and better performance.

Gradient Accumulation

These two blogs helped me out with this part:

It is well known that mini-batch descent produces good results, but sometimes even the mini batch is large in some cases. Like for CV on a 4k image etc. In those scenarios when we lack memory we use Gradient Accumulation to overcome that issue.

Instead of updating the model in every mini batch, we accumulate the gradient over the course of a few batches then update it.

Image of grad accumulation

This essentially acts like a bigger batch

A typical training loop looks like this

for inputs, labels in data_loader:
    output = model(input)

    loss = criterion(output,labels)

    loss.backward()
    optimizer.step()
    optimizer.zero_grad()

But when we do gradient accumulation it looks something like this

acc_steps = 3

for idx, (inputs, labels) in enumerate(data_loader):
    output = model(input)

    loss = criterion(output,labels)

    loss.backward()

    # Only do update the weights if it the last mini batch
    if ((idx + 1) % acc_steps == 0) or (idx + 1 == len(data_loader)):
        optimizer.step()
        optimizer.zero_grad()

Large Batch Training

The authors also noted that large batch training can improve training without the need to do complex techniques.

A quote from the paper

Large batch training can improve training efficiency even without large scale parallel hardware through gradient accumulation, whereby gradients from multiple mini-batches are accumulated locally before each optimization step.

Gradient Checkpointing

There really is no reason to mention this here, But this is a popular method to overcome memory limitations too. So I though I will briefly talk about it.

It is rather straightforward, We know when we train a NN, we need to store the gradients for backpropagation. For large models this can get quite big.S So for some layers instead of storing it, we re-compute it during backprop.

(Obviously much more goes into training the large scale LLMs we use nowdays, we will talk about them as we move forward)

DistilBERT and Model Compression

Image of BERT

Link to paper: DistilBERT, a distilled version of BERT: smaller,faster, cheaper and lighter

Quick Summary

This 2020 paper by Sanh et al. from Hugging Face introduces DistilBERT, a smaller, faster version of BERT created through knowledge distillation. The authors address the growing concern that state-of-the-art NLP models are becoming increasingly large and computationally expensive, limiting their practical deployment, especially on edge devices.

Key contributions:

  1. They create a distilled version of BERT that retains 97% of its language understanding capabilities while being 40% smaller and 60% faster at inference time.

  2. DistilBERT is built using knowledge distillation during the pre-training phase (rather than task-specific distillation), using a triple loss function that combines:

    • The standard masked Language Modeling loss
    • A distillation loss using the teacher’s soft target probabilities
    • A cosine embedding loss to align the directions of the student and teacher hidden states

  3. The student model (DistilBERT) uses the same architecture as BERT but with half the number of layers, and is initialized by taking every other layer from the teacher model.

  4. The authors demonstrate that DistilBERT performs well across various NLP tasks:

    • On GLUE benchmark tasks, it retains 97% of BERT-base’s performance
    • On IMDb sentiment classification, it achieves 92.82% accuracy (vs. 93.46% for BERT-base)
    • On SQuAD question answering, it reaches 85.8 F1 (vs. 88.5 for BERT-base)

  5. They also show that DistilBERT can run effectively on mobile devices, with a model size of 207 MB and 71% faster inference time than BERT on an iPhone 7 Plus.

This work demonstrates that through careful distillation, smaller and more efficient models can be created without significant loss in performance, making state-of-the-art NLP more accessible for resource-constrained applications.


Image of BERT

The following sources helped me immensely while writing this section.

What is Knowledge Distillation

Image of Knowledge Distillation

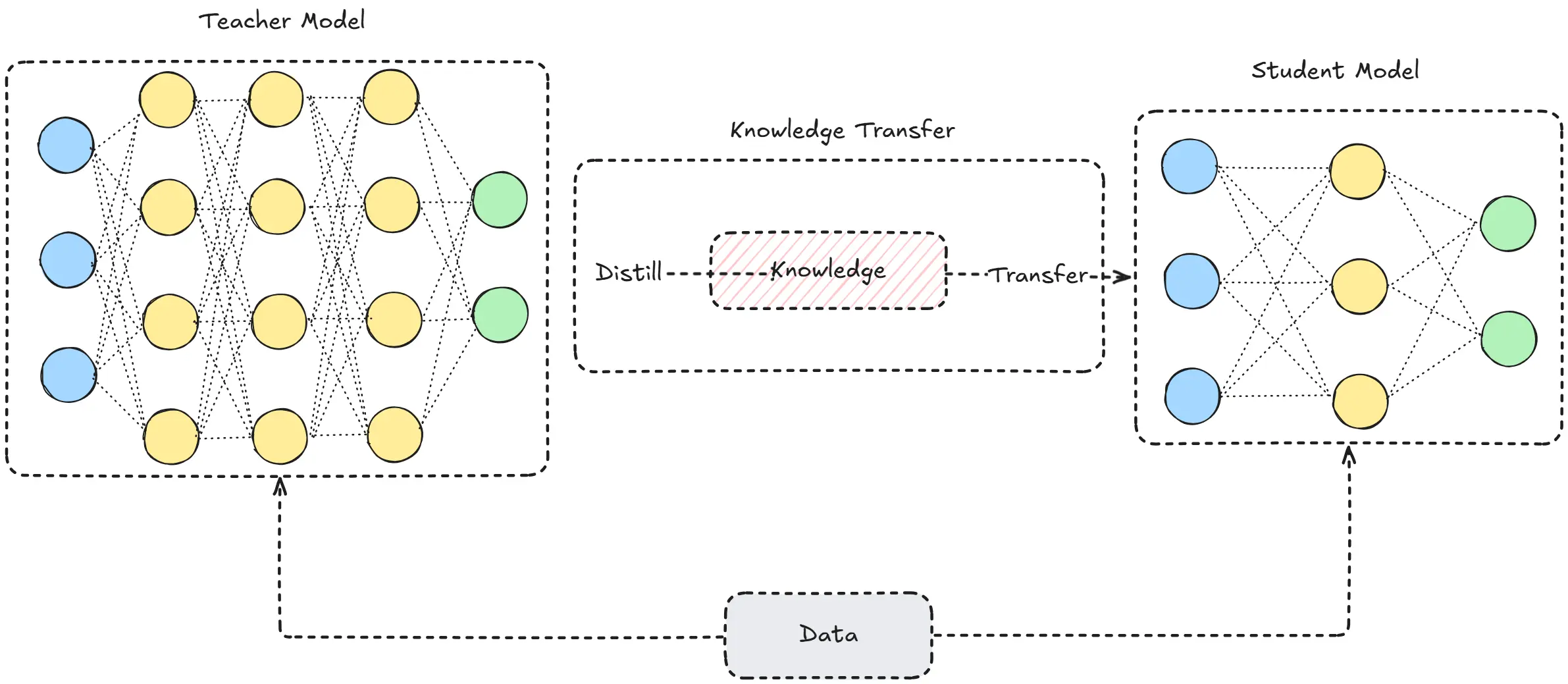
The idea is quite simple we have a big heavy model trained for long period of time on a lot of data, and we want a smaller model to learn from the bigger model.

There are many reasons we may wish to do this, they are cheaper and faster to inference. They can on edge devices like mobiles, watches, drones etc. And most of the times they retain 90+ performance of the original model while being significally smaller.

Types of Knowledge Distillation

Image of different types of knowledge distillation Image taken from paper

There are definitely many kinds of distillation methods available to us (the above image makes it quite obvious). We will not be able to talk about all of them, So I will touch on the most popular one’s and ask you to explore the one’s you find interesting.

Response Based

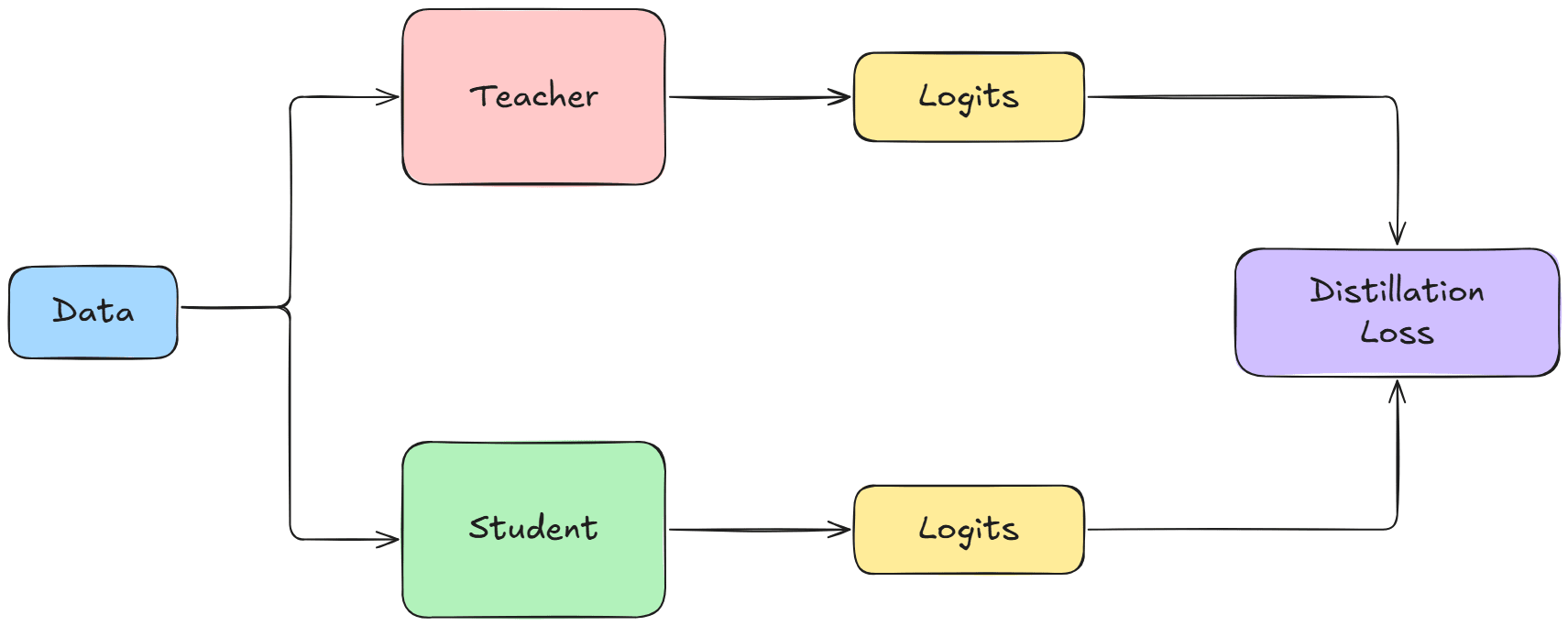
Image of BERT

In this method, we take a sample of training data. Run it by both our models. And then make the smaller model learn the soft labels of the bigger model.

We are essentially trying to make the smaller model predict like the bigger model.

Now one may question what are soft labels, Lets see it with an example

[0,1,0,0] -> hard labels

[0.1,0.3,0.5,0.1] -> soft labels

A model outputs an array of probabilities, out of which many are near zero probabilities. These near zero probabilities still hold a lot of knowledge

For instance an apple can be confused for a red ball, but it should not be confused for the moon.

This is known as dark knowledge. We are essentially trying to make our smaller model learn this dark knowledge.

Hinton et al introduced an idea of temperature to control the importance of these soft labels. As T tends to inifity all latels have the same value

\[p_i = \frac{\exp(z_i/T)}{\sum_j \exp(z_j/T)}\]

Where:

  • $p_i$ is the probability of class $i$
  • $z_i$ is the logit for class $i$
  • $T$ is the temperature parameter

Temperature $T$ controls how “soft” the probability distribution becomes. When $T = 1$, we get the normal softmax. As $T$ increases, the distribution becomes more uniform (softer), revealing the relative similarities between classes that the teacher model has learned. When $T → ∞$, all probabilities approach equal values. During distillation, we use $T > 1$ to extract this “dark knowledge” from near-zero probabilities.

Feature Based

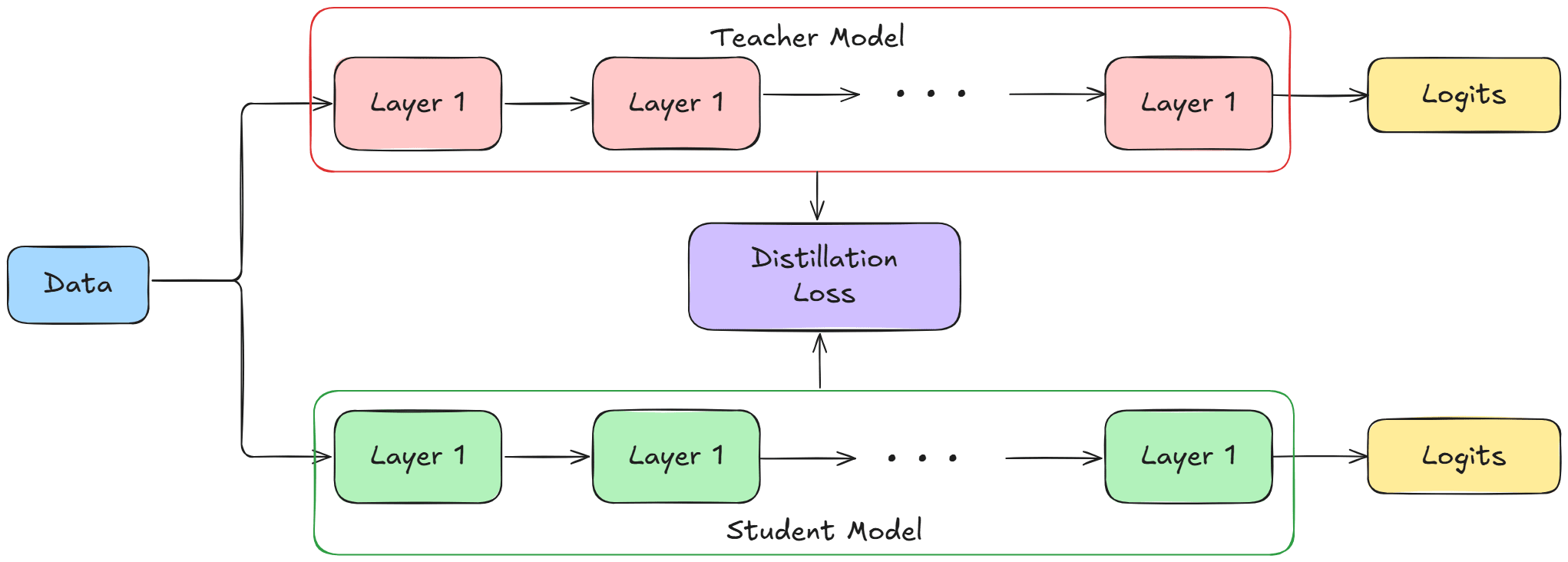
Image of BERT

In this, we hope to replicate the weights of the bigger model in our smaller model. Instead of matching final outputs, we match intermediate representations (feature maps) from corresponding layers of teacher and student models. The student learns to produce similar internal representations as the teacher, capturing how the teacher processes information at different depths. Transformation functions $\Phi_t$ and $\Phi_s$ may be needed when teacher and student have different dimensions.

\[L_{FeaD}(f_t(x), f_s(x)) = L_F(\Phi_t(f_t(x)), \Phi_s(f_s(x)))\]

where:

  • $L_{FeaD}$ is the feature distillation loss
  • $f_t(x)$ and $f_s(x)$ are the teacher and student feature representations
  • $\Phi_t$ and $\Phi_s$ are transformation functions for the teacher and student features
  • $L_F$ is the loss function applied to the transformed features

Relation Based

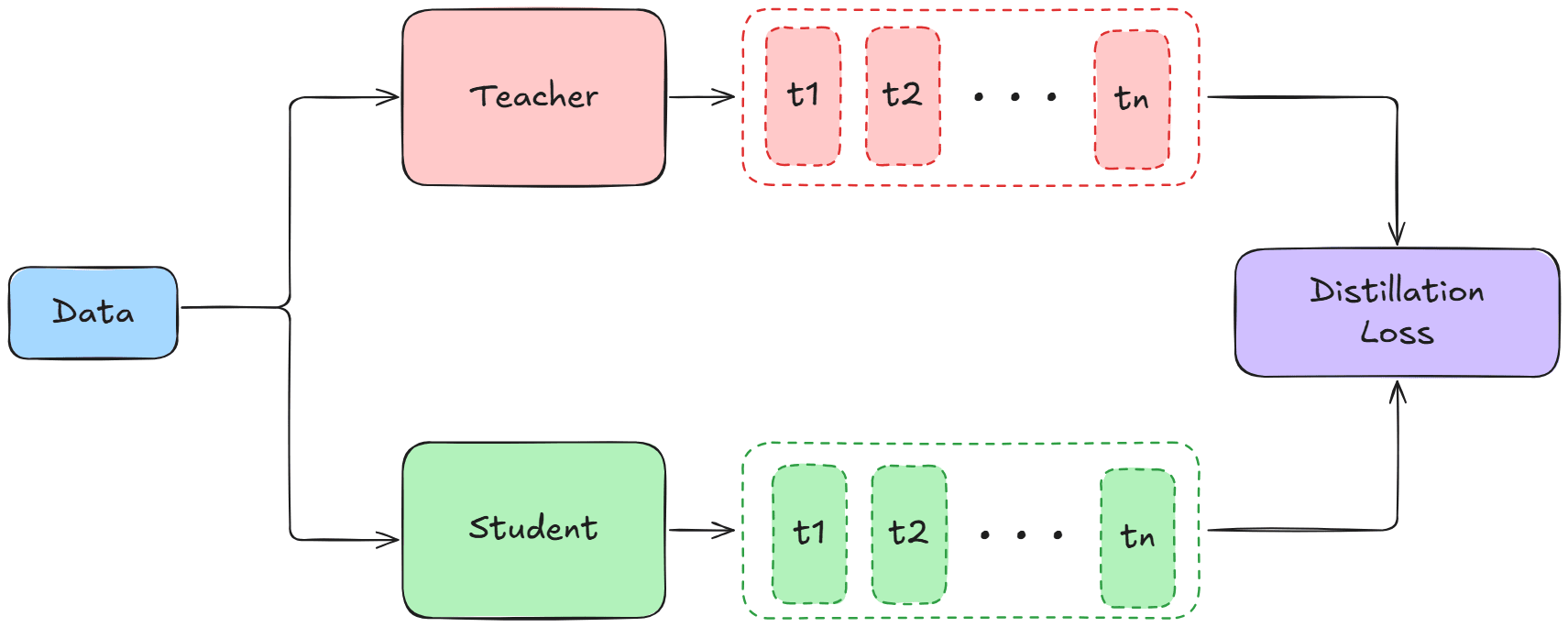
Image of BERT

Take a pair of feature maps from both the models, and minimize the loss between their relationship.

NOTE: Even though feature maps is used both in featured based and realtion based KD, they are quite different. For example in Feature based we are trying to map the exact features to be in the same distribution. But in realtion based, the indiividual values do not matter, the realtion between them does. For example in feature based if Ft(Xt) = 5 then we want Fs(X) = 5 as well. But in Relation Ft(x1,x2) = 5 then Fs(x3,x4) = 5 where the feature maps x by themselves can be quite different

As mentioned earlier, there are a lot of methods available for KD. If you are further intersted, checkout the survey!

How was diltillbert trained

Distillbert was trained using the response based distillation method. KLD is used as the distillation Loss.

import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.optim import Optimizer

KD_loss = nn.KLDivLoss(reduction='batchmean')

def kd_step(teacher: nn.Module,
            student: nn.Module,
            temperature: float,
            inputs: torch.tensor,
            optimizer: Optimizer):
    teacher.eval() # Notice teacher model is in eval mode
    student.train()

    with torch.no_grad():
        logits_t = teacher(inputs=inputs) # Do not store the gradients of teacher
    logits_s = student(inputs=inputs)

    loss = KD_loss(input=F.log_softmax(logits_s/temperature, dim=-1),
                   target=F.softmax(logits_t/temperature, dim=-1)) # KLD loss on teacher output with student output.
                   # Notice how the student output is a log softmax, because we are training it

    loss.backward()
    optimizer.step()
    optimizer.zero_grad()

Code modified from gist

Architecture difference Source

The architecture of distillbert is very similar to BERT, they have reduced the number of layers. Significantly decreasing the amount of parameters (From 110M to 66M), While maintaing 95% performance of BERT. The authors additionally removed the token-type embeddings and the pooler (as there is no Next sentence predition here)

It is interesting to talk about the initialization and training as well. As noted by the author they initialized distillbert by taking the weights of every other layer (as they had common hidden size namely 768). They also trained the model on very large batches, using gradient accumulation, with dynamic masking and NSP removed.

Now let’s talk about the loss used to train DistillBert. They used a triple loss which is a combination of MLM Loss, Distillation Loss & Similarity Loss.

These Beautiful images were taken from this blog

Image of MLM Loss Source

Masked Language Modeling Loss is pretty straight forward and we have already talked about it in our BERT section. In this we do cross entropy over predicted distribution and true distribution.

Image of BERT Source

Distillation loss is an idea that is new here, it is a response based loss, In which we compare the KLD between the Teacher’s output distribution and the Student’s output distribution.

Here KLD and Cross-Entropy has been used interchangably, but that is usually not the case.

KLD and cross-entropy can be used interchangeably only when the one distribution is fixed (Here the teacher distribution). Here’s why:

\[\text{KLD}(p_{teacher} || p_{student}) = \sum_i p_{teacher}(i) \log \frac{p_{teacher}(i)}{p_{student}(i)}\] \[= \sum_i p_{teacher}(i) \log p_{teacher}(i) - \sum_i p_{teacher}(i) \log p_{student}(i)\]

Since the teacher’s distribution is fixed during training, the first term $\sum_i p_{teacher}(i) \log p_{teacher}(i)$ is constant and can be ignored for optimization purposes. The remaining term $-\sum_i p_{teacher}(i) \log p_{student}(i)$ is exactly the cross-entropy loss. Therefore, minimizing KLD is equivalent to minimizing cross-entropy in this context.

Image of BERT Source

Cosine embedding loss is straight forward as well, here we just take the cosine distance between the embedding vector.

Remember the embedding matrix is also a learned parameter!

Image of BERT Source

In the end, we put all of it together and train DistillBERT!!!

If you would like to distill a model, this is a good tutorial by PyTorch. Furthermore this was a nice paper on distillation scalling laws, consider checking it out!

BART

Image of BART

Link to paper: BART: Denoising Sequence-to-Sequence Pre-training for Natural Language Generation, Translation, and Comprehension

Quick Summary

The paper introduces BART (Bidirectional and Auto-Regressive Transformers), a denoising autoencoder for pretraining sequence-to-sequence models. BART works in two stages:

  1. It first corrupts text with various noising functions (like token masking, deletion, text infilling, sentence shuffling)
  2. Then it learns to reconstruct the original text

BART combines the bidirectional encoding approach of BERT with the autoregressive generation capabilities of GPT. This architecture makes it particularly effective for both text generation and comprehension tasks. The authors evaluate various noising approaches and find that randomly shuffling sentences combined with a novel text infilling scheme (replacing spans with mask tokens) works best.

In experiments, BART achieves strong performance across multiple NLP tasks:

  • Matching RoBERTa on classification tasks like GLUE and SQuAD
  • Achieving new state-of-the-art results on summarization tasks (with up to 6 ROUGE point improvements)
  • Showing effectiveness for dialogue, question answering, and even machine translation

The paper presents a thorough ablation study comparing BART to other pretraining approaches and demonstrates its versatility as a general-purpose language model.


BART is not as complex as the ideas we have discussed so far, reading the summary above should be enough.

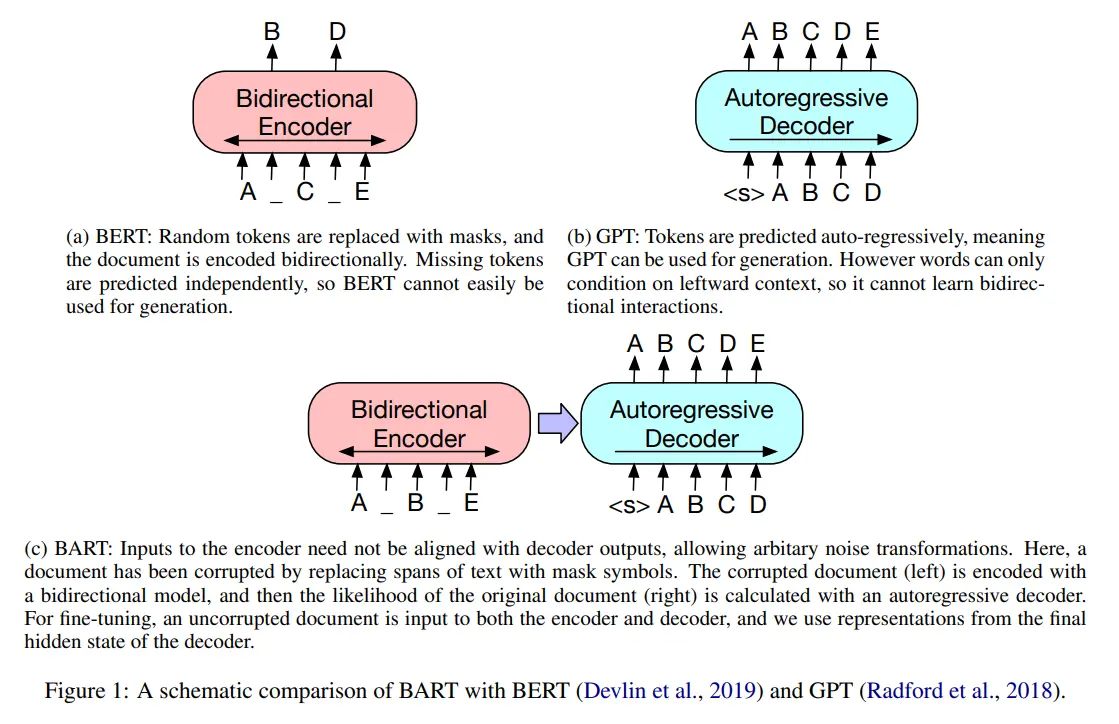
Image of BART

In simple terms BART is just BERT + GPT. The novel idea it introduced was in it’s training. Where corrupted data was given as the input and using reconstruction loss (Cross entropy over predicted and original data distribution), the outputs were predicted.

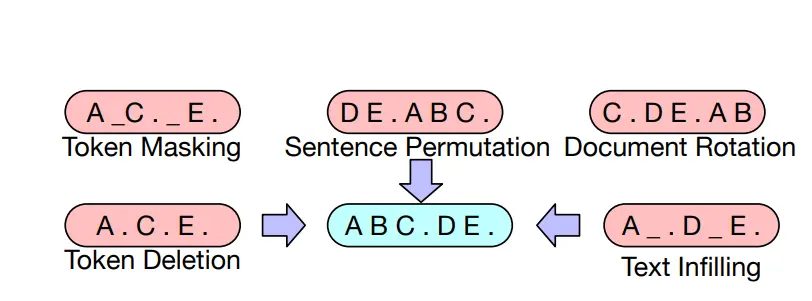
Image of BART

Most of the noise and corruption is self explanatory from the above image, except text infilling. So let us talk about that for a moment.

In it we take a text (Pizza is the most delicious dish in the world) and we sample a span, whose length is drawn from a Poisson distribution ($\lambda=3$). These spans (Pizza is/delicious/in the world) are then masked ([MASK] the most [MASK] dish [MASK]).

In the current age, The BART architecture never gained popularity. I believe partly due to it’s complexity. There is nothing else left to discuss so I’ll be skipping the fine-tuning method. If you wish to know more about it, consider going through the paper.

Transformer-XL

Image of Transformer-XL

Link to paper: Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context

Quick Summary

This paper introduces Transformer-XL, a novel neural architecture that addresses a key limitation of standard Transformers in language modeling: their inability to capture dependencies beyond a fixed context length.

Key Problems Solved

Context Fragmentation: Traditional Transformers process text in fixed-length segments without information flow between segments, leading to inefficient optimization and poor prediction of tokens at segment boundaries.

Limited Dependency Length: Vanilla Transformers can only model dependencies within their fixed context window, typically a few hundred tokens.

Main Innovations

  1. Segment-Level Recurrence Mechanism
  • Reuses hidden states from previous segments as extended context for the current segment
  • Enables modeling of much longer dependencies (80% longer than RNNs, 450% longer than vanilla Transformers)
  • Creates a recurrent connection between segments while maintaining the parallelization benefits of self-attention
  1. Relative Positional Encoding
  • Replaces absolute positional encodings with relative ones to enable state reuse
  • Decomposes attention into four intuitive terms: content-based addressing, content-dependent positional bias, global content bias, and global positional bias
  • Allows models trained on shorter sequences to generalize to longer ones during evaluation

Results

Transformer-XL achieved state-of-the-art results across multiple datasets:

  • WikiText-103: 18.3 perplexity (previous best: 20.5)
  • enwiki8: 0.99 bits per character (first to break 1.0)
  • One Billion Word: 21.8 perplexity
  • Up to 1,874x faster evaluation speed compared to vanilla Transformers

Technical Contributions

The architecture maintains gradient flow within segments while allowing information to propagate across segments through cached hidden states. The relative positional encoding scheme ensures temporal coherence when reusing states and generalizes well to longer contexts than seen during training.

Impact

Transformer-XL demonstrated the ability to generate coherent text spanning thousands of tokens and established new benchmarks for long-range dependency modeling. The techniques introduced became influential for subsequent developments in large language models, particularly for handling longer contexts efficiently.

The paper represents a significant step forward in extending the effective context length of Transformer-based models while maintaining computational efficiency.


Problem The big problem with vanilla transformers was their fixed context length. During training and inference, they could only pay attention to a limited chunk of text at a time, like reading a book through a keyhole. Any information outside that small window was completely invisible.

This method of splitting text into rigid segments also caused context fragmentation. Imagine a sentence being cut in half between two segments. The model would struggle to understand the beginning of the second segment because it couldn’t see the end of the first one, leading to poor performance and inefficient training.

Solution

  1. A method to pass information through the segments
  2. Novel Positional Encoding Scheme

Image of Fixed context window Source

The above image is of a traditional model during it’s train and evaluation phase. Notice the segments, you will see that Segment 2 [$X_5$ to $X_8$] have no information passed from Segment 1 [$X_1$ to $X_4$]. This leads to two problems, first being we can only use our model withing a limited context window, Outside which we won’t be able to run it. The other being of data fragmentation, I.E text data is highly connected and breaking it into segments can break the flow of information (Something present in the first segment which is relevant to the third segment won’t be present in it!)

To solve this problem, the authors introduced two ideas

Segment-level Recurrence

Image of Fixed context window Source

In this during the train phase, after a segment is processed, its calculated hidden states are cached and reused as an extended context for the next segment. When the model processes the new segment, it can attend to both its own tokens and the tokens from the previous segment’s cache.

Crucially, the gradients only flow through the current segment. The cached states are “frozen,” acting as a read-only memory. This allows the model to learn from past information without the massive computational cost of backpropagating through the entire sequence, similar in spirit to truncated backpropagation in RNNs.

Relative Positional Encodings

There is still one minor problem that needs to be addressed. Back then, fixed positional encoding used to be used in models (Read this if you are new to this idea).

It assigns a unique embedding to each position (e.g., position 1, position 2, etc.). This breaks when we introduce recurrence.

  • Segment 1 has tokens at positions 1, 2, 3, 4
  • Segment 2 also has tokens at positions 1, 2, 3, 4

When we process Segment 2, the model sees the token at absolute position 5 (the first token of Segment 2) and the token at absolute position 1 (the first token of Segment 1). But both are labeled with the same positional encoding for “position 1”. The model has no way to tell them apart, leading to what the paper calls temporal confusion.

And the authors solve it using Relative Positional Encoding. Ok, this part get’s kind of tough, so bear with me as I walk you through step by step

Step 1: The Math of a Standard Transformer

In a standard Transformer, the input for a token at a specific position i is the sum of its word embedding and its positional embedding:

\[X_i = E_i + U_i\]

Here, $E_i$ is the word embedding (the token’s meaning), and $U_i$ is the absolute positional embedding (the token’s fixed address in the sequence).

The Query and Key vectors are linear transformations of this input:

\(Q_i = (E_i + U_i)W_q\) \(K_j = (E_j + U_j)W_k\)

The attention score is the dot product of a specific Query vector $Q_i$ with a specific Key vector $K_j$. If we expand this dot product, we reveal four distinct components that the model uses to calculate attention:

\[A_{i,j}^{\text{abs}} = ( (E_i + U_i)W_q )^\top ( (E_j + U_j)W_k )\] \[A_{i,j}^{\text{abs}} = \underbrace{E_i^\top W_q^\top W_k E_j}_{\text{(a) content-content}} + \underbrace{E_i^\top W_q^\top W_k U_j}_{\text{(b) content-position}} + \underbrace{U_i^\top W_q^\top W_k E_j}_{\text{(c) position-content}} + \underbrace{U_i^\top W_q^\top W_k U_j}_{\text{(d) position-position}}\]

The problem lies in terms (b), (c), and (d), which all rely on the absolute position vectors $U_i$ and $U_j$. This rigid system breaks when we use recurrence, as the model can’t distinguish between position 5 in segment one and position 5 in segment two.

Step 2: Rebuilding the Attention Score for Transformer-XL

To solve this, Transformer-XL re-engineers the attention score to be based only on relative distances, removing all absolute positional information. This is done by carefully modifying each of the four terms.

The new formula is:

\[A_{i,j}^{\text{rel}} = \underbrace{E_i^\top W_q^\top W_{k,E} E_j}_{\text{(a) content-based addressing}} + \underbrace{E_i^\top W_q^\top W_{k,R} R_{i-j}}_{\text{(b) content-dependent positional bias}} + \underbrace{\mathbf{u}^\top W_{k,E} E_j}_{\text{(c) global content bias}} + \underbrace{\mathbf{v}^\top W_{k,R} R_{i-j}}_{\text{(d) global positional bias}}\]

Let’s break down the changes:

  1. Replacing Absolute Positions: The key’s absolute position vector $U_j$ is replaced with a relative position vector $R_{i-j}$. This vector encodes the distance between the query i and the key j (e.g., “3 steps behind”).

  2. Splitting the Key Matrix: The key weight matrix $W_k$ is split into $W_{k,E}$ for producing content-based keys and $W_{k,R}$ for producing location-based keys.

  3. Removing the Query’s Position: The query’s absolute position term ($U_i^\top W_q^\top$) is entirely replaced by two trainable parameter vectors, $\mathbf{u}$ and $\mathbf{v}$. These act as global biases.

    • Term (c) now represents a global bias for the content of the key word.
    • Term (d) now represents a global bias for the relative distance to the key word.

With these changes, the attention score no longer depends on where a token is, but only on what it is and how far away it is from other tokens. This elegant solution makes the attention mechanism compatible with the segment-level recurrence that allows Transformer-XL to see beyond a fixed context.

The above is definitely as straight forward as some of the other concepts we have talked about so far, so take your time trying to understand it.

XLNet

Image of XLNet

Link to paper: XLNet: Generalized Autoregressive Pretraining for Language Understanding

Quick Summary

XLNet is a novel approach to pretraining language models that combines the advantages of both autoregressive (AR) language models like GPT and autoencoding (AE) models like BERT, while avoiding their limitations.

The key innovation of XLNet is its permutation Language Modeling objective. Rather than using a fixed left-to-right order like traditional autoregressive models, XLNet maximizes the expected log likelihood over all possible permutations of the factorization order for a sequence. This allows each token to effectively see context from both directions while maintaining the autoregressive property.

XLNet addresses two key limitations of BERT:

  1. It eliminates the independence assumption BERT makes during training (where masked tokens are predicted independently)
  2. It avoids the pretrain-finetune discrepancy caused by the artificial [MASK] tokens used in BERT

Key architectural components include:

  • A two-stream attention mechanism that creates separate content and query streams to enable target-aware predictions
  • Integration of Transformer-XL for better handling of long sequences
  • Relative positional encodings and relative segment encodings for improved generalization

In empirical evaluations, XLNet outperforms BERT on 20 tasks including question answering, natural language inference, sentiment analysis, and document ranking, often by substantial margins.


It’s hard to break this paper down into a problem and solution segment, As the broader idea was “Both Auto-regressive (Decoder only) & Auto-Encoding (Encoder Only) have their pros and cons, but how do we bring the best of both worlds together”. This is not an easy paper by a long shot. I will try my best to explain it as well as I can.

First we need to understand the pros and cons of AR & AE models as identified by the authors

AE Pros & Cons

Pros:

  • It is bidirectional by nature, so it can understand information from both direction

Cons:

  • Independence Assumption: BERT assumes all masked tokens are predicted independently of each other. For the phrase “New York,” if both words are masked, BERT doesn’t use its prediction for “New” to help it predict “York”.

  • Pretrain-Finetune Discrepancy: The artificial [MASK] symbol used during pre-training is absent during fine-tuning, creating a mismatch that can affect performance.

AR Pros & Cons

Pros:

  • Captures the sequential nature of natural language, i.e one word comes after the other.

Cons:

  • It is unidirectional, meaning it can only process context from one direction (either left-to-right or right-to-left), which is a disadvantage for many downstream tasks. For example classification

To address the cons of BERT it uses an AR model, and to make it bidirectional. The authors introduce a new idea called Permutation Language Modeling objective.

In this instead of training our models in sequential form 1,2,3,4 and so on. It is instead trained on all possible permutations of the sequence. For example 4,2,1,3/2,4,3,1/1,4,2,3 and many more. Now it is a common source of confusion that the data it self is scrambled. But there is no augmentation done in the data or position encoding side. The embeddings themselves and their positions remain the same.

Instead the attention values are masked. Let us understand how.

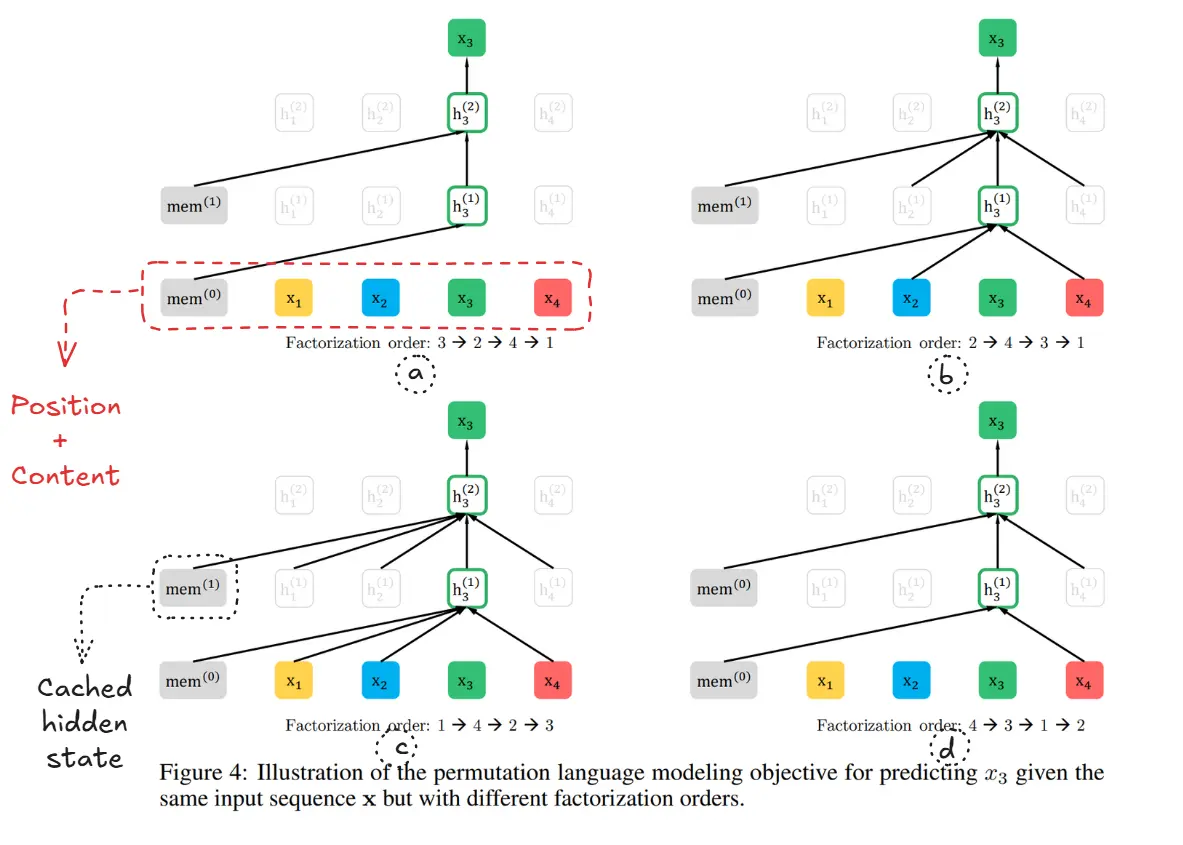Image of Megatron Modified from source

This looks extremely convoluted, I know!! But let’s go through it one by one.

To understand how masking achieves this, let’s look at the image below, which shows how the model predicts the token at position 3 (x₃) under different factorization (prediction) orders.

This looks complex, but the logic is simple: a token can only see other tokens that come earlier in the random permutation order.

  • In panel (a), the order is 3 → 2 → 4 → 1. Since x₃ is the first token to be predicted, its context is empty.

  • In panel (b), the order is 2 → 4 → 3 → 1. Here, x₃ is the third token to be predicted, so it can see the context from the first two predicted tokens, x₂ and x₄.

By doing this over and over with random orders, the model learns that any token can be surrounded by any other token, forcing it to learn a rich, bidirectional understanding of the language.

P.S. mem here is the cached hidden state from the previous segment, an idea inspired by Transformer-XL

Image of Megatron Source

The permutation objective creates a challenge: To predict a token at a target position, the model needs to know the position, but it cannot know the content of the token at that position (otherwise, it would just copy it). A standard Transformer can’t do this, as its hidden state at any position always contains both content and position information.

To solve this, XLNet introduces a Two-Stream Self-Attention mechanism.

Content Stream h (The Memory) This is the standard Transformer representation. It encodes both the content and position of a token. Its job is to serve as the rich context, or “memory,” that other tokens can attend to. In the image, this is what the nodes labeled h represent.

Query Stream g (The Predictor) This is a special representation that only has access to the target position, not its content. Its entire purpose is to gather information from the Content Stream of its context tokens to make a prediction for the target position. In the image, this is what the nodes labeled g represent.

In simple terms, for each token being predicted, the Query Stream g asks the question, and the Content Stream h of the other tokens provides the answer. At the final layer, the output of the Query Stream is used to predict the word. During fine-tuning, the query stream is discarded, and we use the powerful, bidirectionally-trained Content Stream for downstream tasks.

Megatron

Image of Megatron

Link to paper: Megatron-LM: Training Multi-Billion Parameter Language Models Using Model Parallelism

Quick Summary

The Megatron-LM paper presents an approach for training extremely large language models using model parallelism that enables training transformer models with billions of parameters. Let me explain the key aspects of this work:

Core Innovation: Simple and Efficient Model Parallelism

The authors implement a simple but effective model parallel approach where they split transformer layers across multiple GPUs in a way that minimizes communication overhead. They do this through:

  1. Intra-layer model parallelism: Rather than splitting entire layers across GPUs (pipeline parallelism), they split individual operations within transformer layers.

  2. Strategic tensor partitioning: Matrices in transformer layers are partitioned along specific dimensions to minimize communication:

    • In the MLP blocks, the first GEMM is split column-wise and the second GEMM is split row-wise
    • In self-attention, they partition across attention heads, allowing each GPU to process different attention heads

  3. Communication optimization: They carefully place all-reduce operations to minimize the number of synchronization points needed between GPUs.

  4. Duplicate computation: Instead of communicating for small operations like dropout or layer normalization, they duplicate these computations across GPUs.

Scaling Achievements

  • They established a strong baseline by training a 1.2 billion parameter model on a single GPU that achieves 39 TeraFLOPs (30% of theoretical peak)
  • They scaled to an 8.3 billion parameter model using 512 GPUs with 8-way model parallelism and 64-way data parallelism
  • They achieved 15.1 PetaFLOPs sustained performance with 76% scaling efficiency compared to the single GPU case

Architecture Innovation for BERT Models

The authors discovered that the standard BERT architecture suffers from degradation when scaled beyond the BERT-Large size. They fixed this by rearranging the layer normalization and residual connections in the architecture, enabling larger BERT models to achieve consistently better results.

Results

Their models achieved state-of-the-art results on:

  • WikiText103 (10.8 perplexity vs previous SOTA of 15.8)
  • LAMBADA (66.5% accuracy vs previous SOTA of 63.2%)
  • RACE dataset (90.9% accuracy vs previous SOTA of 89.4%)

The paper demonstrates that with the right implementation approach, training multi-billion parameter language models is feasible, and these larger models lead to superior performance on a wide range of NLP tasks.


This is a great time to talk about data, model and pipeline paralism and how massively large LLMs are trained across GPUs, Because that is what essential the NVIDIA team did with megatron and shared how they did it!

Obviously Parallel training of huge models on large clusters is a MEGA topic, and we can write books on it. (There are companies and books made on it). So my objective here will be to introduce you to the various concepts of model parallalism, going a bit overboard on what was done in megatron too (for brevity’s sake)

Let us start with the idea of megatron training and we can build on top of that

note: the paper talks about two main ideas, training & how they improved performance on BERT. We will only focus on training in this blog. If you are curious about BERT modifications. Check out the paper!

Now to be complete, We also need to talk about how we can calculate the amount of VRAM required before we start with distributed training. Lest you get too many or too less GPU (Compute is extremely expensive, so we gotta be mindful of what we have)

These are the rough GPU memory requirements:

  • FP16 parameter ~ 2 bytes
  • FP16 gradient ~ 2 bytes
  • FP32 optimizer state ~ 8 bytes based on the Adam optimizers
  • FP32 copy of parameter ~ 4 bytes (needed for the optimizer apply (OA) operation)
  • FP32 copy of gradient ~ 4 bytes (needed for the OA operation)

Even for a relatively small DL model with 10 billion parameters, it can require at least 200GB of memory, which is much larger than the typical GPU memory (for example, NVIDIA A100 with 40GB/80GB memory and V100 with 16/32 GB) available on a single GPU. Note that on top of the memory requirements for model and optimizer states, there are other memory consumers such as activations generated in the forward pass. The memory required can be a lot greater than 200GB. (Taken from sagemaker AWS documentation)

If you want to understand the memory better I will recommend the following blogs:

Some Misc blogs I found while researching the GPU memory problem:

The following blogs and articles were insanely helpful, While writing the below section:

  • This blog gave a great TL;DR with pseudocode (The code in this section has been taken/inspired from here)
  • Great overview documentation by HF.
  • AWS Documentationhad some nice animations with practical code that helped me understand stuff.
  • This blog acted as an awesome glossary and gave good summaries of the ideas.
Naive Parallalism

Naive Model Prallelism, is well… naive and straightforward. Here you just cut the layers of a large model. And put it in different GPUs sequentially.

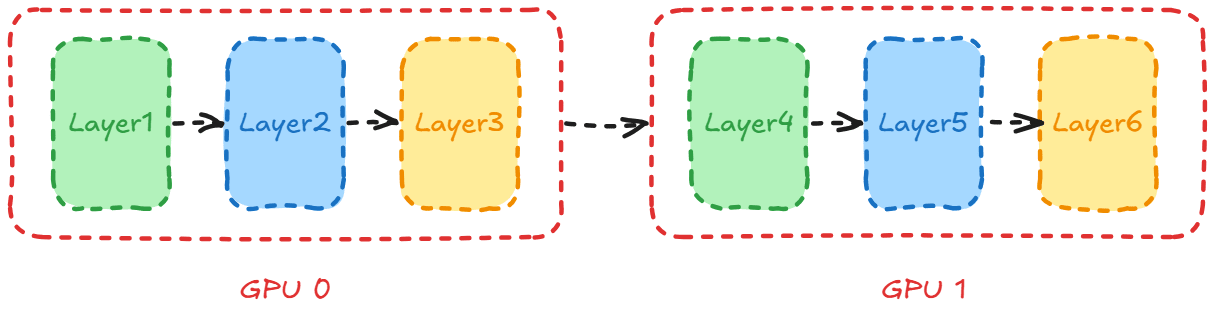Image of Megatron Inspired from here

The implementation is simple as well, you just keep changing the device using .to(), But there are a few problems. The first one being, when the data travels from layer 0 upto layer 3. It is pretty fast as they are in the same device, but when it needs to go to layer 4, this introduced a computational overhead. If both the GPUs are not in the same machine, this will make it very slow.

Another problem is, even though we have 2 devices, while the data is being transfered from layer1 to layer3. The other GPUs remain idle. To fix these problems, the idea of pipeline parallelism was introduced.

# Define model portions
model_part1 = nn.Sequential(layer1, layer2).to('cuda:0')
model_part2 = nn.Sequential(layer3, layer4).to('cuda:1')

# Forward pass
def forward(x):
    x = model_part1(x)
    x = x.to('cuda:1')
    return model_part2(x)

Code taken from here

Pipeline Parallelism

Image of Megatron Source

Piepline Parallelism is very similar to Naive MP, We the models split in this too. But to solve the idling problem. The data is sent in mini batches. So each GPU has access to some part of the data and they work somewhat concurrently.

There is an obvious bubble present though, that happens when one GPU is waiting for the gradients to do backprop. In practice, an ideal size of batch along with numbers of GPU is calculated so when one forward pass is completed, mini batch of calculated results keep coming back.

# Define stages
stage1 = nn.Sequential(layer1, layer2).to('cuda:0')
stage2 = nn.Sequential(layer3, layer4).to('cuda:1')

# Pipeline forward
def pipeline_forward(batches):
    for i, batch in enumerate(batches):
        x = stage1(batch)
        x = x.to('cuda:1')
        if i > 0:
            yield stage2(prev_x)
        prev_x = x
    yield stage2(prev_x)

Code taken from here

Data Parallelism

Image of Megatron Source

This is another simple method of parallelism. Each device has a full copy of the model, and the data is split between them. And at the end the gradients are synchronized together.

# On each device
for batch in dataloader:
    outputs = model(batch)
    loss = criterion(outputs, targets)
    loss.backward()

    # Synchronize gradients across devices
    all_reduce(model.parameters.grad)

    optimizer.step()

Code taken from here

Tensor Parallelism

Image of Megatron source

This is the kind of parallelism first introuduce by the megatron paper.

This is a great read on the topic as well github comment.

In this you partition the individual tensors (weights, activations) across devices. And each device computes a portion of the tensor.

This was beautifully explained by the paper, Imagine you have to do an operation (as shown in the above image). We can simply break the matrix and compute it in different devices and put it back together.

Parallelizing the MLP Block

An MLP block contains two linear layers. The first is a GEMM (GEneral Matrix Multiply) followed by a GeLU nonlinearity:

\[Y = \text{GeLU}(XA)\]

To parallelize this across two GPUs, the authors split the weight matrix $A$ column-wise: $A = [A_1, A_2]$. The input $X$ is fed to both GPUs, and each computes its part of the operation:

\[[Y_1, Y_2] = [\text{GeLU}(XA_1), \text{GeLU}(XA_2)]\]

This is efficient because the GeLU activation can be applied independently on each GPU without any communication.

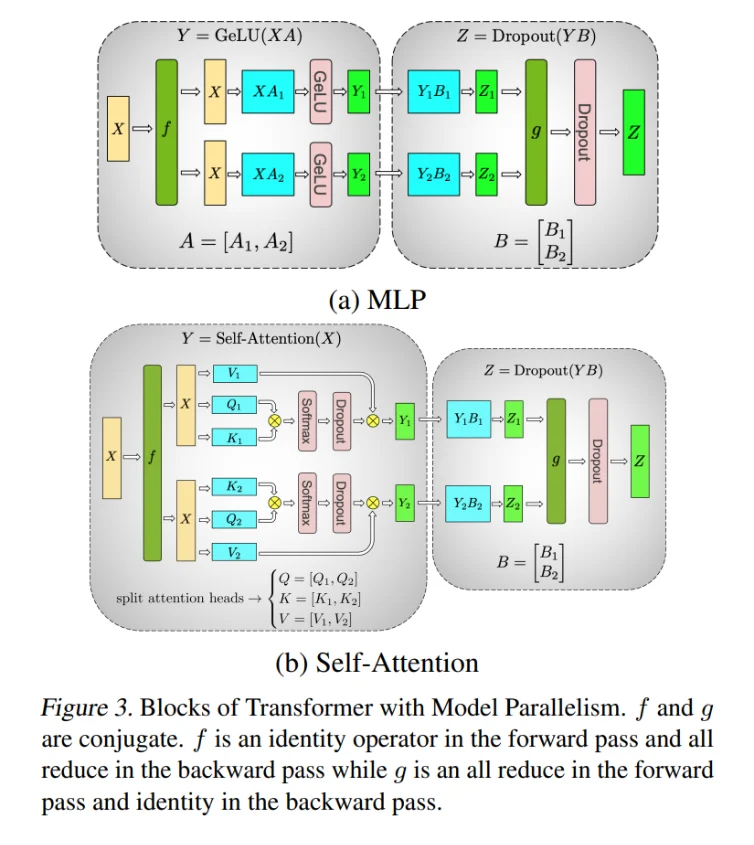
Image of Megatron

The second linear layer in the MLP block involves another GEMM, $Z = YB$. To make this work, the second weight matrix $B$ is split row-wise:

\[B = \begin{bmatrix} B_1 \\ B_2 \end{bmatrix}\]

Each GPU then computes its part, and the results are summed up using an all-reduce operation across the GPUs. This all-reduce is the only communication needed in the forward pass for the MLP block.

Parallelizing the Self-Attention Block

The same principle is applied to the self-attention mechanism. The large weight matrices for Query, Key, and Value ($W_Q, W_K, W_V$) are split column-wise across the GPUs, partitioned by the number of attention heads. Each GPU can compute its share of attention heads independently.

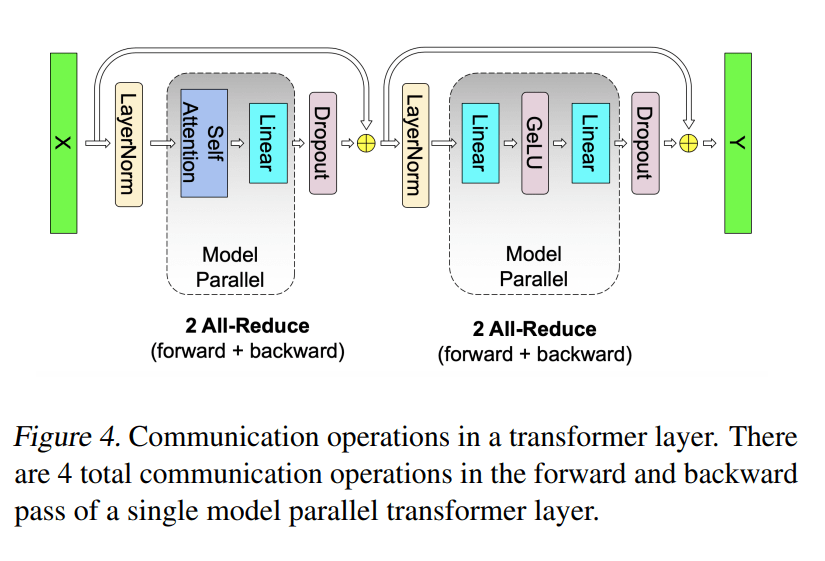
Image of Megatron

Just like in the MLP block, the output linear layer is split row-wise, and a single all-reduce operation synchronizes the results at the end.

The key takeaway is that this method cleverly arranges the matrix splits so that a full Transformer layer only requires two all-reduce operations in the forward pass (one for the MLP, one for attention) and two in the backward pass. This minimizes communication overhead and leads to excellent scaling efficiency.

# Simplified tensor parallel linear layer
class TPLinear(nn.Module):
    def __init__(self, in_features, out_features, n_devices):
        super().__init__()
        self.weight = nn.Parameter(torch.randn(out_features // n_devices, in_features))

    def forward(self, x):
        local_out = F.linear(x, self.weight)Z
        return all_gather(local_out)

Code taken from here

2d parallalism & 3d parallalism

I mentioned it here to keep you aware of these ideas, we will discuss in depth about them later on. But for now a simple deifition is enough.

  • 2d parallism -> When you use two of the techniques described above together.
  • 3d parallism -> following the above definition when you use 3 of the above described techniques together it’s called 3d parallism.

There is also ZeRO but we will talk about it when we get to that section.

For a deeper dive into how to implement each and use them in your application, check out the documentation by the PyTorch Team.

Additionally I will recommend checking these two phenomenol blogs by an engineer at Anthropic.

The code behind Megatron-LM

Sparse Attention Patterns

Image of Megatron

Link to paper: Generating Long Sequences with Sparse Transformers

  • Reduced computational complexity for long sequences
Quick Summary

This 2019 paper by Rewon Child, Scott Gray, Alec Radford, and Ilya Sutskever from OpenAI introduces Sparse Transformers, an architectural innovation that makes Transformers more efficient for modeling very long sequences.

Key innovations:

  • Introduces sparse factorizations of the attention matrix that reduce computational complexity from O(n²) to O(n√n)
  • Proposes architectural modifications to train deeper networks
  • Implements memory-efficient recomputation of attention matrices
  • Develops fast attention kernels for training

The authors demonstrate that Sparse Transformers can effectively model sequences of tens of thousands of timesteps using hundreds of layers. They apply the same architecture to model images, audio, and text from raw bytes, achieving state-of-the-art results on density modeling tasks for Enwik8, CIFAR-10, and ImageNet-64. Notably, they show it’s possible to use self-attention to model sequences of length one million or more.


Problem

Transformers are awesome, and we all love them (otherwise, you wouldn’t be reading such a huge blog on the topic). But they face one big issue: the self-attention calculation has a quadratic time and memory complexity, which becomes impractical for very long sequences.

Solution

The authors introduce sparse factorization methods to the attention mechanism, reducing its complexity to $O(N\sqrt{N})$. They additionally introduce fast custom kernels and a recomputation method (gradient checkpointing) to save memory.

The following blogs helped me immensely while writing this section:

The Cost of Full Attention

If you’ve read this far, I am going to assume you have a fair bit of knowledge about computer science. One of the earliest ideas talked about in CS101 is Big O notation. So let’s quickly calculate the complexity of self-attention.

The self-attention mechanism can be expressed as:

\[\text{Attention}(Q, K, V) = \text{Softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V\]

Let’s break down the computational complexity step-by-step for a sequence of length $N$:

  1. Computing $QK^T$: The multiplication of a $[N \times d_k]$ matrix ($Q$) with a $[d_k \times N]$ matrix ($K^T$) results in an $[N \times N]$ attention matrix. The complexity is $O(N^2 \cdot d_k)$.
  2. Scaling and Softmax: These are element-wise operations on the $[N \times N]$ matrix, so their complexity is $O(N^2)$.
  3. Multiplying with V: Multiplying the $[N \times N]$ attention matrix with the $[N \times d_v]$ value matrix ($V$) has a complexity of $O(N^2 \cdot d_v)$.

Since the hidden dimensions $d_k$ and $d_v$ are considered constants with respect to the sequence length, the dominant factor is $N^2$. The overall complexity of self-attention is:

\[O(N^2)\]

This quadratic cost is computationally expensive for large $N$. This is where Sparse Attention comes in, reducing the complexity to a more manageable $O(N\sqrt{N})$.

Building the Sparse Patterns

The objective of this blog is to help you believe you could have come up with these ideas on your own. So let’s begin by understanding the rationale of the researchers. By visualizing the attention patterns of a deep, fully-trained Transformer, they noticed some recurring themes.

Attention mask img Image taken from the paper, Figure 2

a) Many early layers learned local patterns, resembling convolutions.
b) Some layers learned to attend to entire rows and columns, effectively factorizing the attention.
c) Deeper layers showed global, data-dependent patterns.
d) Surprisingly, the deepest layers exhibited high sparsity, with positions activating rarely.

From these observations, we get a sense of the useful patterns: we need something local, something that can access information globally, and perhaps something in between, like a stride.

Attention mask img Image taken from the paper, Figure 3

This image might look daunting, but it’s quite simple if we break it down. Let’s quickly clarify the two rows of images. The top row shows the perspective of a single output element (the dark blue square) and which input elements (the light blue squares) it can attend to. The bottom row provides a holistic view of the entire sequence’s connectivity matrix.

Now, let’s look at the patterns:

(b) Strided Attention This pattern combines two kinds of attention. One head focuses on a local window of nearby positions. For example, the i-th position might only attend to keys from i-w to i, where w is the window size. The other head focuses on more global interactions by having the i-th query attend to every c-th key, where c is the stride. This captures both local context and a coarser, long-range context.

This method works very well for data with a natural periodic structure, like images (where a pixel is related to its neighbors and also to the pixel directly above it). However, it can fail when it comes to text. The reason is that relationships in text are not based on fixed intervals; a word’srelevance to another isn’t determined by a consistent spatial coordinate or stride.

(c) Fixed Attention To solve the problem with text, the authors introduced “fixed attention.” This also uses a local window, but the second head is different. Instead of a stride, it has all future positions attend to a few fixed “summary” locations from previous block.

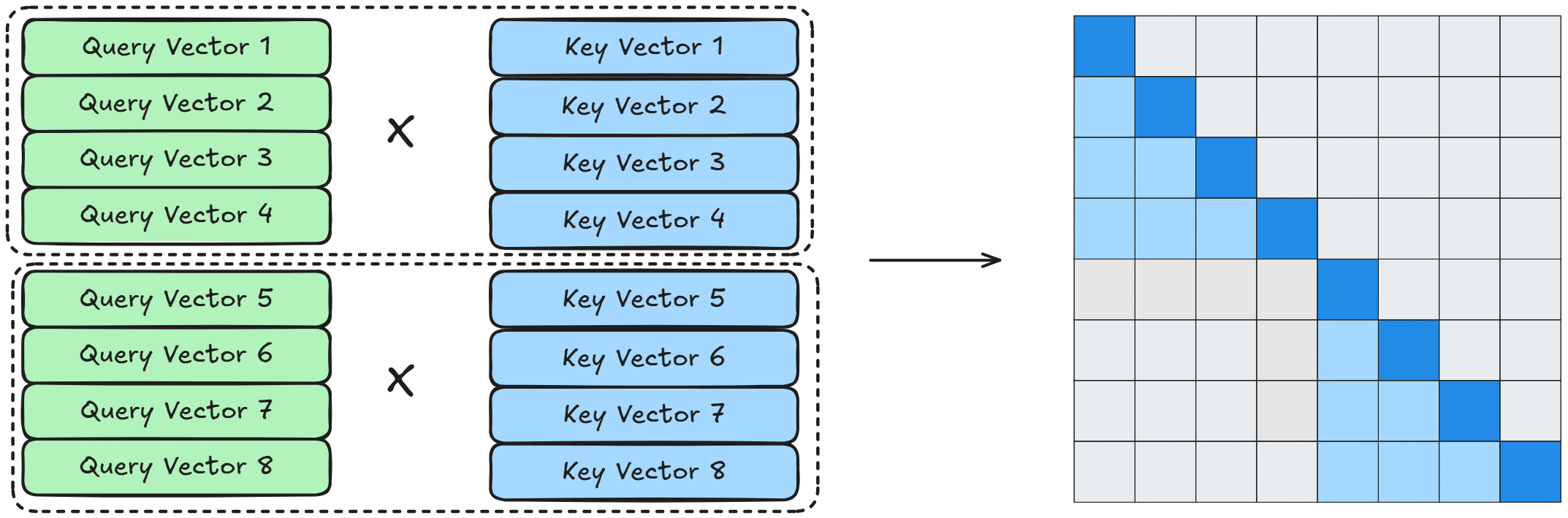Attention mask img Inspired from here

The local attention creates the block-like structure. This works well but has one big issue: each block only has information from within its own block.

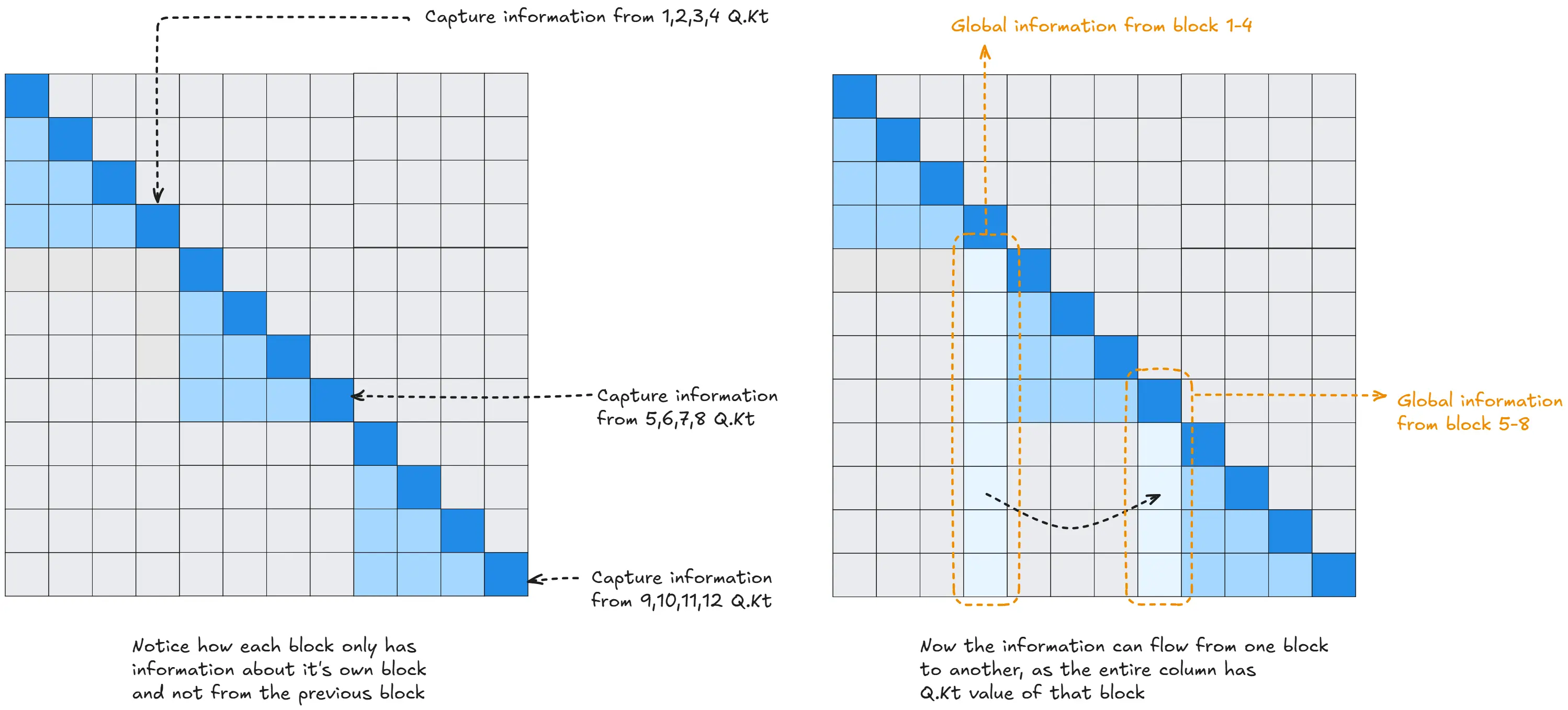Attention mask img Inspired from here

The fixed summary positions act as “global connectors.” Information captured by the end of a block can now flow globally to all subsequent blocks, allowing the model to connect ideas across the entire sequence.

Calculating the Complexity of Sparse Attention

These sparse patterns significantly reduce the computational cost. Let’s see how, using the formulas from the paper.

In the strided case, each query attends to a local window of size $w$ and roughly $N/c$ strided positions, where $c$ is the stride. The total cost for $N$ queries is:

\[N \left( w + \frac{N}{c} \right) \sim O(N\sqrt{N}), \quad \text{if } c = \sqrt{N}\]

In the fixed case, the sequence is split into blocks of length $l$. Each query attends to at most $l$ local positions and $c$ summary positions. The total cost for all queries is:

\[N(l+c) \sim O(N\sqrt{N}), \quad \text{if } l = \sqrt{N}\]

In both cases, by carefully choosing the hyperparameters, we can achieve the desired sub-quadratic complexity of $O(N\sqrt{N})$.

Some other ideas introduced in the paper as stated by the authors include:

• A restructured residual block and weight initialization to improve training of very deep networks • A set of sparse attention kernels which efficiently compute subsets of the attenion matrix • Recomputation of attention weights during the backwards pass to reduce memory usage

If you wish to check out the work done by OpenAI, you can do so here: Sparse Attention Repo. They also open-sourced their work on fast kernels: Blocksparse Repo.

NOTICE: Build first, Write later

This blog is now on a short hiatus, I give my reasons here. I will still continue updating this blog, but not as often. Thank you for reading everything I write. P.S. I am putting out all of the unstructured thoughts and content below for anyone who is curious to check out the resources I had collected for each section

2020: The Scale Revolution

Reformer

Image of Reformer

Link to paper: Reformer: The Efficient Transformer

Quick Summary

This 2020 ICLR paper introduces the Reformer, a more memory-efficient and computationally efficient variant of the Transformer architecture. The authors (Kitaev, Kaiser, and Levskaya) address key bottlenecks in standard Transformers:

  1. The quadratic memory and computation requirements of self-attention (O(L²) where L is sequence length)
  2. The memory needed to store activations for all layers during backpropagation
  3. The large memory footprint of feed-forward layers

Their solution combines two main innovations:

  • Replacing standard dot-product attention with a locality-sensitive hashing (LSH) based attention mechanism, reducing complexity from O(L²) to O(L log L)
  • Using reversible residual layers that allow recovering activations during backpropagation without storing them, significantly reducing memory requirements

The authors show that Reformer achieves comparable performance to standard Transformers while enabling training on much longer sequences (up to 64K tokens) and with substantially lower memory usage. They demonstrate results on text (enwik8) and image generation (ImageNet-64) tasks.


https://www.youtube.com/watch?app=desktop&v=i4H0kjxrias&t=0s&ab_channel=YannicKilcher

https://www.pinecone.io/learn/series/faiss/locality-sensitive-hashing/ https://jaketae.github.io/study/lsh/

https://research.google/blog/reformer-the-efficient-transformer/

https://raviteja-ganta.github.io/Reformer-The-efficient-Transformer

Longformer

Image of Longformer

Link to paper: Longformer: The Long-Document Transformer

Quick Summary

The Longformer paper addresses a key limitation of traditional Transformer models: their quadratic computational complexity with respect to sequence length, which makes processing long documents prohibitively expensive. The authors introduce a novel attention mechanism that scales linearly with sequence length, enabling the processing of documents with thousands of tokens.

Key innovations:

  1. Attention mechanism: Longformer uses a combination of:

    • Sliding window attention: Each token attends to a fixed window of surrounding tokens
    • Dilated sliding window: Increases receptive field without increasing computation by adding gaps between attended tokens
    • Global attention: Task-specific tokens (like [CLS] or question tokens in QA) can attend to the entire sequence

  2. Efficient implementation: Custom CUDA kernels enable processing sequences of up to 32K characters

  3. Performance: Longformer achieves:

    • State-of-the-art results on character-level Language Modeling (text8 and enwik8)
    • Outperforms RoBERTa on long document tasks
    • Sets new state-of-the-art results on WikiHop and TriviaQA

  4. Longformer-Encoder-Decoder (LED): A variant for sequence-to-sequence tasks like summarization

The paper demonstrates both the theoretical and practical advantages of this approach across multiple tasks including classification, question answering, and coreference resolution.


GShard

Image of Gshard

Link to paper: GShard: Scaling Giant Models with Conditional Computation and Automatic Sharding

https://www.youtube.com/watch?v=1VdEw_mGjFk&ab_channel=YannicKilcher

Quick Summary

GShard addresses critical scaling challenges in training extremely large neural network models. The paper introduces a module that enables efficient training of models with hundreds of billions to trillions of parameters through:

  1. Conditional computation - Using Sparsely-Gated Mixture-of-Experts (MoE) layers where only a subset of the model is activated for each input, allowing computation to scale sublinearly with model size

  2. Automatic sharding - A separation between model description and parallelization implementation through simple annotation APIs that allow the XLA compiler to automatically partition computation across thousands of accelerators

  3. Single Program Multiple Data (SPMD) - A compiler technique that generates a single program to run on all devices, keeping compilation time constant regardless of the number of devices

The effectiveness of GShard is demonstrated through multilingual machine translation experiments, where they trained a 600 billion parameter Transformer model with MoE layers on 2048 TPU v3 accelerators in just 4 days. This model achieved superior translation quality across 100 languages compared to both bilingual baselines and dense Transformer models, while using less computational resources.

Key benefits of the approach include:

  • Sublinear scaling of computation relative to model size
  • Constant memory usage per device as model size increases
  • Efficient training with little communication overhead
  • Easy-to-use APIs that separate model description from parallelization implementation


RAG (Retrieval-Augmented Generation)

Image of RAG

Link to paper: Retrieval-Augmented Generation for Knowledge-Intensive NLP Tasks

Quick Summary

This paper introduces RAG (Retrieval-Augmented Generation), a hybrid model architecture that combines the strengths of parametric memory (knowledge stored in neural network parameters) and non-parametric memory (knowledge stored in an external database that can be retrieved).

The key innovation is a framework where:

  1. A retriever component fetches relevant passages from a large corpus (Wikipedia)
  2. A generator component (BART) uses both the input query and retrieved passages to produce outputs
  3. The entire pipeline is trained end-to-end, treating the retrieved documents as latent variables

The authors explore two model variants:

  • RAG-Sequence: uses the same retrieved document for generating the entire output sequence
  • RAG-Token: can use different documents for generating different tokens in the output

They evaluate RAG on knowledge-intensive tasks including open-domain QA, fact verification, and knowledge-grounded generation, achieving state-of-the-art results on several benchmarks. One particularly interesting aspect is that RAG’s non-parametric memory can be easily updated (by changing the retrieval corpus) without retraining the model.


Big Bird

Image of Big Bird

Link to paper: Big Bird: Transformers for Longer Sequences

Quick Summary

The paper introduces BigBird, a sparse attention mechanism for transformer models that reduces the quadratic dependency on sequence length to linear, enabling the processing of sequences up to 8x longer than previously possible with similar hardware.

Key Innovations:

BigBird’s sparse attention mechanism consists of three main components:

  1. Global tokens - A set of g tokens that attend to all parts of the sequence
  2. Window attention - All tokens attend to a set of w local neighboring tokens
  3. Random attention - All tokens attend to a set of r random tokens

Theoretical Contributions:

The authors provide theoretical guarantees for BigBird, showing that:

  1. It’s a universal approximator of sequence functions
  2. It’s Turing complete, preserving the expressive properties of full attention models
  3. Their theoretical analysis reveals the benefits of global tokens for maintaining expressivity

Experimental Results:

BigBird shows significant improvements in tasks requiring longer contexts:

  1. Question Answering - Achieves state-of-the-art results on various datasets (HotpotQA, Natural Questions, TriviaQA, WikiHop)
  2. Document Summarization - Outperforms previous methods on long document summarization tasks (Arxiv, PubMed, BigPatent)
  3. Genomics Applications - Novel application to DNA sequences, improving performance on promoter region prediction (99.9% F1) and chromatin profile prediction

Technical Details:

  • The paper addresses implementation details for efficiently computing the sparse attention on GPUs/TPUs through “blockification” of the attention pattern
  • The authors prove there’s “no free lunch” - showing a natural task where sparse attention mechanisms require polynomially more layers compared to full attention
  • Their approach balances theoretical guarantees with practical efficiency


Problem

””” Unfortunately, one of their core limitations is the quadratic dependency (mainly in terms of memory) on the sequence length due to their full attention mechanism. “””

Solution

””” , BIGBIRD, a sparse attention mechanism that reduces this quadratic dependency to linear “””

https://huggingface.co/blog/big-bird

GPT-3

Image of gpt-3

Link to paper: Language Models are Few-Shot Learners

  • In-context learning
  • Few-shot capabilities
  • Scaling laws discovery
  • Batch size scaling
Quick Summary

Key Contributions

This paper demonstrates how scaling up language models to unprecedented sizes (175B parameters, 10x larger than previous models) enables significant improvements in few-shot learning capabilities. The authors show that large language models can perform tasks with few or no examples through “in-context learning,” where the model adapts to new tasks simply by being conditioned on examples in its prompt, without parameter updates.

Main Findings

  1. Scaling Laws: Performance on various tasks improves smoothly with model size, following predictable power-law scaling trends.

  2. Few-Shot Learning: GPT-3 can perform impressively on numerous tasks with just a few examples in the context, sometimes matching or approaching state-of-the-art fine-tuned models.

  3. Zero-Shot and One-Shot: Even with no examples (zero-shot) or just one example (one-shot), GPT-3 shows remarkable capabilities.

  4. Versatility: GPT-3 demonstrates strong performance across a wide range of NLP tasks including question answering, translation, common sense reasoning, reading comprehension, and more.

  5. Emergent Abilities: Certain capabilities like arithmetic, novel word usage, and unscrambling words emerge more strongly at the largest model sizes, suggesting qualitative improvements beyond simple scaling.

Key Results Across Task Categories

  • Language Modeling: Sets new SOTA on Penn Tree Bank perplexity (20.5)
  • Cloze and Completion Tasks: Substantial improvements on LAMBADA (86.4% accuracy)
  • Question Answering: Competitive with fine-tuned systems on TriviaQA (71.2%)
  • Translation: Approaches SOTA unsupervised NMT results
  • Winograd-Style Tasks: Strong performance (88.6% on Winograd, 77.7% on Winogrande)
  • Common Sense Reasoning: State-of-the-art on PIQA (82.8%)
  • Reading Comprehension: Strong results on CoQA (85.0 F1)
  • SuperGLUE: Competitive with fine-tuned BERT-Large

Limitations

The authors transparently address several limitations:

  1. GPT-3 still struggles with some tasks requiring complex reasoning, bidirectional context, or specialized knowledge.

  2. The model shows some biases in gender, race, and religion reflective of its training data.

  3. Even at this scale, sample efficiency during pre-training is much less than human learning.

  4. Some tasks still show a large gap between few-shot performance and fine-tuned models.

Broader Impacts

The paper discusses potential misuse concerns and ethics issues, including biases in the model and potential for generating misleading content. The authors conducted experiments showing that humans can distinguish GPT-3-generated news articles from human-written ones only at chance levels.

Significance

This work represents a paradigm shift in how we think about language models - rather than fine-tuning smaller models for specific tasks, it suggests that scaling up models enables general in-context learning abilities that can be applied to many tasks without task-specific training.


Rethinking Attention with Performers

Image of Performer

Link to paper: Rethinking Attention with Performers

https://medium.com/analytics-vidhya/paper-explained-rethinking-attention-with-performers-b207f4bf4bc5

https://www.youtube.com/watch?v=xJrKIPwVwGM&ab_channel=YannicKilcher

Quick Summary

This 2021 ICLR paper introduces the Performer, a Transformer architecture that can estimate regular (softmax) attention with provable accuracy while achieving linear (rather than quadratic) space and time complexity. The key innovation is the FAVOR+ (Fast Attention Via positive Orthogonal Random features) mechanism, which enables efficient approximation of softmax attention kernels without assumptions about sparsity or low-rankness.

The paper makes several key contributions:

  1. A new method for approximating softmax attention using positive orthogonal random features
  2. Linear-time complexity attention mechanism that’s fully compatible with regular Transformers
  3. Strong theoretical guarantees on the quality of the approximation
  4. The ability to efficiently model kernelizable attention mechanisms beyond softmax

The authors demonstrate the Performer’s effectiveness on diverse tasks from pixel prediction to protein sequence modeling, showing competitive results with other efficient attention methods while enabling much longer sequence lengths.


T5

Image of Longformer

Link to paper: Exploring the Limits of Transfer Learning with a Unified Text-to-Text Transformer

  • Encoder-decoder architecture
  • Unified text-to-text framework
  • Span corruption
  • Multi-task pre-training

””” Link: https://huggingface.co/docs/transformers/model_doc/t5 Family: Transformer Pretraining Architecture: Encoder/Decoder Pretraining Task: DAE Extension: Same as original Transformer with some additions such as relative positional embeddings like Transformer XL Application: General language tasks including machine translation, question answering, abstractive summarization, and text classification Date (of first known publication): 10/2019 Num. Params: 11 B (up to) Corpus: Colossal Clean Crawled Corpus (C4) — Cleaned up version of the Common Crawl dataset — 750 GB License: Open, Apache-2.0 Lab: Google “””

Quick Summary

This 2020 paper by Raffel et al. introduces the “Text-to-Text Transfer Transformer” (T5), a unified approach to transfer learning for NLP tasks. The authors convert all text-based language problems into a consistent text-to-text format, where both inputs and outputs are always text strings. This allows them to use the same model, loss function, and training procedure across diverse tasks.

The paper presents a comprehensive empirical study examining various aspects of transfer learning for NLP, including:

  1. Model architectures
  2. Pre-training objectives
  3. Pre-training datasets
  4. Transfer approaches
  5. Scaling effects

They introduce the “Colossal Clean Crawled Corpus” (C4), a massive dataset of cleaned web text for pre-training. By combining insights from their systematic study with scale (training models up to 11 billion parameters), they achieve state-of-the-art results on many NLP benchmarks including GLUE, SuperGLUE, SQuAD, and CNN/DailyMail summarization.

The T5 approach demonstrates the effectiveness of a unified text-to-text framework for transfer learning across diverse NLP tasks, showing that with the right architecture and sufficient scale, a single approach can excel across the NLP landscape.


https://cameronrwolfe.substack.com/p/t5-text-to-text-transformers-part

Measuring Massive Multitask Language Understanding

Image of Longformer

Link to paper: Measuring Massive Multitask Language Understanding

(benchmark)

Quick Summary

This 2021 paper introduces a comprehensive benchmark for evaluating language models’ multitask capabilities across 57 diverse subjects. The authors (Hendrycks et al.) created a test covering fields like STEM, humanities, social sciences, and professional domains at varying levels of difficulty, from elementary to advanced professional knowledge.

The key findings show that while smaller models performed near random chance (25% on multiple-choice questions), the largest GPT-3 model (175B parameters) achieved 43.9% accuracy - significantly better than random but still far below expert-level performance (estimated at ~90%). Performance was notably lopsided across subjects, with calculation-heavy topics like physics and mathematics showing poor results, as did socially important subjects like law and morality.

The research highlights several important insights about large language models circa 2021:

  1. Models struggled with procedural knowledge vs. declarative knowledge
  2. Models were often miscalibrated (not knowing when they don’t know)
  3. Even the largest models failed to exhibit expert-level performance in any subject
  4. The benchmark required diverse world knowledge beyond commonsense reasoning

This work provided an important evaluation framework showing that while large language models were beginning to demonstrate impressive capabilities, they still had fundamental limitations in their ability to learn and apply specialized knowledge.


ZeRO (Zero Redundancy Optimizer)

https://dev.to/lewis_won/data-parallelism-4g3m

Image of ZeRO

Link to paper: ZeRO: Memory Optimizations Toward Training Trillion Parameter Models

  • Memory optimization for distributed training
Quick Summary

This paper introduces ZeRO (Zero Redundancy Optimizer), a memory optimization system designed to overcome memory limitations in training extremely large deep learning models.

Key Contributions:

  • ZeRO enables training models with billions to trillions of parameters by eliminating memory redundancies in data-parallel and model-parallel training
  • The approach maintains high computational efficiency while drastically reducing memory requirements
  • ZeRO includes different optimization stages that can provide up to linear memory reduction with the number of devices
  • The authors demonstrate training models with over 100B parameters with super-linear speedup on 400 GPUs
  • ZeRO enables training large models (up to 13B parameters) without model parallelism, making it more accessible
  • ZeRO powered the creation of Turing-NLG (17B parameters), which at the time was the world’s largest language model

The paper presents an elegant solution to a fundamental bottleneck in large model training, showing how clever memory management can effectively scale model size proportional to the number of available devices.


https://oracle-oci-ocas.medium.com/zero-redundancy-optimizers-a-method-for-training-machine-learning-models-with-billion-parameter-472e8f4e7a5b

https://www.youtube.com/watch?v=KgoHyMGpxBU&ab_channel=nPlan

https://alessiodevoto.github.io/parallelism/ -> Great blog on ZeRO

https://www.microsoft.com/en-us/research/blog/zero-deepspeed-new-system-optimizations-enable-training-models-with-over-100-billion-parameters/

https://huggingface.co/docs/transformers/v4.15.0/parallelism

ELECTRA

Image of ELECTRA

Link to paper: ELECTRA: Pre-training Text Encoders as Discriminators Rather Than Generators

Google’s model that used a discriminative approach instead of masked Language Modeling, providing more efficient training As noted, “Electra deploys a ‘Masked Language Modeling’ approach that masks certain words and trains the model to predict them. Additionally, Electra incorporates a ‘Discriminator’ network that aids in comprehending language without the need to memorize the training data.”

Quick Summary

ELECTRA presents a more efficient alternative to masked Language Modeling (MLM) pre-training methods like BERT. Instead of masking tokens and training a model to predict the original ones, ELECTRA proposes “replaced token detection” - a discriminative task where:

  1. A small generator model replaces some tokens with plausible alternatives
  2. A discriminator model (ELECTRA) learns to distinguish between original and replaced tokens

The key advantages of this approach are:

  • It’s more computationally efficient since the model learns from all input tokens rather than just the 15% that are masked
  • It achieves better downstream performance given the same compute budget
  • It works particularly well for smaller models, enabling high-quality language models to be trained on a single GPU

The authors demonstrate ELECTRA’s efficiency by showing it outperforms BERT, GPT, and other models when controlling for compute. For example, ELECTRA-Small trained on one GPU for 4 days outperforms GPT (trained with 30x more compute) on the GLUE benchmark.


Switch Transformer

paper

Google’s early mixture-of-experts approach that demonstrated trillion-parameter scale was possible

Quick Summary

This paper introduces the Switch Transformer, an architecture that simplifies the Mixture of Experts (MoE) approach to create more efficient and scalable language models. The key innovation is routing tokens to exactly one expert (rather than multiple experts) at each layer, which the authors call “switching.” This approach:

  1. Significantly increases parameter count while keeping computational costs fixed
  2. Achieves better performance per FLOP than dense models
  3. Offers training speedups of up to 7x compared to T5 models with the same computational budget
  4. Scales effectively to trillion-parameter models

The authors demonstrate that even with as few as two experts, their approach shows improvements over standard Transformers. They also introduce techniques to improve training stability, including selective precision for routing operations and expert dropout for fine-tuning.


Scaling Laws

paper

OpenAI’s publication on the mathematical relationships between model size, dataset size, and computational budget demonstrated predictable patterns for improving performance This was part of the GPT-3 research which showed “that scaling up language models greatly improves task-agnostic, few-shot performance.”

Quick Summary

This 2020 paper by Kaplan, McCandlish, et al. from OpenAI demonstrates that language model performance follows remarkably consistent power-law relationships across multiple dimensions of scale. The authors show that model loss decreases as a power-law function of three key factors: model size (number of parameters), dataset size, and amount of compute used for training.

Their key findings include:

  1. Performance improves smoothly and predictably as model size, dataset size, or compute increases
  2. Model architecture details matter far less than scale factors
  3. Larger models are more sample-efficient than smaller models
  4. When optimizing for compute efficiency, it’s better to train very large models and stop before convergence
  5. The relationship between these factors allows optimal allocation of resources for a given compute budget

The paper’s most striking insight is that these relationships hold across several orders of magnitude, suggesting fundamental scaling properties of neural language models that could inform how we approach building larger and more capable models.


2021: Instruction Tuning and Alignment

RoFormer: Enhanced Transformer with Rotary Position Embedding

paper

Quick Summary

This paper introduces RoFormer (Rotary Position Embedding), a novel technique for encoding positional information in transformer models. The key innovation is representing token positions using rotation matrices, which elegantly captures both absolute position information and relative position relationships between tokens. Unlike previous approaches that often add position embeddings to token representations, RoFormer multiplies token representations by rotation matrices, preserving their norms while encoding position.

The authors demonstrate that RoFormer has several compelling properties:

  • It naturally handles variable sequence lengths
  • It models decreasing attention between tokens as their distance increases
  • It can be integrated with linear self-attention variants, unlike many other position embedding schemes
  • It yields improved performance on long text classification and machine translation tasks

This approach appears to be a mathematically elegant reformulation of positional encoding in transformers that addresses limitations of previous methods while maintaining or improving performance.


https://huggingface.co/blog/designing-positional-encoding

Efficient Large-Scale Language Model Training on GPU Clusters Using Megatron-LM

paper

Quick Summary

This 2021 paper from NVIDIA, Stanford, and Microsoft researchers addresses the critical challenge of efficiently training extremely large language models (LLMs) with billions to trillions of parameters. The authors present a combined parallelization approach they call PTD-P that integrates:

  1. Pipeline Parallelism (P): Distributing layers across GPUs
  2. Tensor Parallelism (T): Splitting individual operations within layers
  3. Data Parallelism (D): Processing different batches on different GPUs

The paper demonstrates impressive scaling to 3072 NVIDIA A100 GPUs, achieving 502 petaFLOP/s performance (52% of theoretical peak) when training a 1 trillion parameter model. They introduce an interleaved pipeline schedule that improves throughput by over 10% and carefully analyze the tradeoffs between different parallelization strategies.

Their approach makes training trillion-parameter models practical (estimated 3 months for full training), which was a significant advancement at publication time. The work includes both theoretical analysis and empirical validation of their proposed methods.


Transcending Scaling Laws with 0.1% Extra Compute

paper

Quick Summary

This 2022 paper from Google introduces UL2R (UL2 Restore), a method that significantly improves large language models with minimal additional computation. The key idea is remarkably simple yet effective: taking a pre-trained language model (like PaLM) and continuing its training for a small number of steps using a mixture of different training objectives called “mixture-of-denoisers.”

The authors demonstrate that applying UL2R to PaLM (creating “U-PaLM”) yields impressive results:

  • With just 0.1% additional compute, they achieve significant performance improvements across various NLP tasks
  • At the 540B parameter scale, U-PaLM achieves performance equivalent to the final PaLM model with approximately half the computational budget (saving ~4.4 million TPUv4 hours)
  • U-PaLM demonstrates “emergent abilities” on challenging tasks, sometimes achieving strong performance at smaller model scales (62B) compared to the original model at larger scales (540B)
  • The technique enables additional capabilities like bidirectional infilling, which allows the model to fill in blanks in the middle of text (not just generate continuations)

This approach is particularly interesting because it challenges conventional wisdom about scaling laws by showing that strategic changes to training objectives can significantly improve efficiency beyond what simply scaling up with more compute would achieve.


Improving language models by retrieving from trillions of tokens

paper

Quick Summary

This 2021 paper from DeepMind introduces Retrieval-Enhanced Transformer (RETRO), a novel approach to Language Modeling that enhances traditional transformer architectures with retrieval capabilities from massive text databases.

Key Innovations:

  • RETRO models can retrieve from databases with trillions of tokens, effectively scaling the data available to the model by an order of magnitude beyond what can be consumed during training
  • The architecture uses a “chunked cross-attention” mechanism to efficiently incorporate retrieved passages into the language model
  • RETRO achieves performance comparable to models with 25× more parameters (e.g., similar to GPT-3 and Jurassic-1 despite using far fewer parameters)
  • The approach effectively creates a semi-parametric model, combining the strengths of parametric models with explicit retrieval

Significance:

The paper demonstrates that retrieval offers an orthogonal scaling dimension to simply increasing model parameters, potentially providing a more efficient path to improving language model capabilities. It shows strong performance on downstream tasks like question answering while maintaining the flexibility to be used with or without retrieval at evaluation time.


CLIP

https://openai.com/index/clip/ Briefly talk about

I have talked more extensively about it in this blog, so I will be skipping it here.

I mentioned it because it was still a very significant work and you should be aware that it came out in this period of time

Dall-e

Briefly talk about

I have an entire blog dedicated to diffusion models, consdier checking that out for more information on the topic.

From now on this blog will solely talk about developments in LLMs, for more general GenAI evolution. I will be writing another blog.

FSDP

paper

Quick Summary

This paper introduces PyTorch’s Fully Sharded Data Parallel (FSDP), an industry-grade solution for training large-scale deep learning models. The technique addresses a critical challenge in the field: enabling the training of models that are too large to fit on a single GPU device.

The key innovation of FSDP is that it decomposes models into smaller units and shards parameters across multiple devices, materializing the full parameters only when needed during computation. The paper details how FSDP has been carefully co-designed with PyTorch’s core components (tensor implementation, dispatcher system, and CUDA memory caching allocator) to provide efficient training while maintaining user-friendly experiences.

The authors explain various optimizations in FSDP including deferred initialization, configurable sharding strategies, communication-computation overlapping, and memory management techniques. Their evaluations show that FSDP achieves comparable performance to Distributed Data Parallel (DDP) for smaller models while enabling training of significantly larger models with near-linear TFLOPS scaling.


https://engineering.fb.com/2021/07/15/open-source/fsdp/

HumanEval

paper

Quick Summary

This paper introduces Codex, a GPT language model fine-tuned on publicly available code from GitHub, and evaluates its capabilities in generating functional Python code. Here’s a high-level summary:

The authors present Codex, a model derived from GPT and fine-tuned on GitHub code repositories. They evaluate Codex’s ability to generate working code by creating HumanEval, a benchmark consisting of 164 hand-written programming problems with unit tests. Unlike previous evaluations based on similarity metrics like BLEU score, they focus on functional correctness - whether the generated code passes the test cases.

Key findings:

  • Codex-12B (12 billion parameters) solves 28.8% of the problems with a single generation attempt
  • When allowed to sample 100 solutions per problem, Codex solves 70.2% of problems
  • They also created a variant (Codex-S) further fine-tuned on correctly implemented standalone functions, which improves performance to 37.7% on single attempts
  • The paper discusses limitations including difficulty with complex docstrings and binding operations to variables
  • The authors conduct a thorough analysis of potential broader impacts including safety, security, and economic implications

This represents a significant step in code generation capabilities, moving beyond simple pattern matching to more sophisticated problem-solving, though still with substantial limitations.


LoRA

paper

Quick Summary

This 2021 paper by Hu et al. from Microsoft introduces Low-Rank Adaptation (LoRA), an efficient fine-tuning method for large language models. The key innovation is freezing the pre-trained model weights while adding trainable low-rank decomposition matrices to each layer of the Transformer architecture.

The main benefits of LoRA include:

  1. Drastically reducing the number of trainable parameters (by up to 10,000x compared to full fine-tuning)
  2. Reducing GPU memory requirements (by up to 3x)
  3. Allowing quick task-switching by only swapping the small LoRA modules
  4. No additional inference latency compared to fully fine-tuned models
  5. Competitive or better performance than full fine-tuning across various models (RoBERTa, DeBERTa, GPT-2, and GPT-3)

The core insight is that while language models are heavily over-parameterized, the changes during adaptation have a low “intrinsic rank.” LoRA exploits this by representing weight updates as low-rank decompositions (BA, where B and A are small matrices). The authors show that surprisingly small rank values (r=1 to r=4) often suffice for strong performance, even for models as large as GPT-3 175B.

The paper includes extensive empirical validation across multiple models and tasks, an analysis of why low-rank updates work well, and discussion of the relationship between the original weights and LoRA updates.


Self-Instruct: Aligning Language Models with Self-Generated Instructions

paper

Quick Summary

This 2023 ACL paper by Wang et al. introduces SELF-INSTRUCT, a framework that improves instruction-following capabilities of pretrained language models by bootstrapping off their own generations. The key innovation is creating a semi-automated process that generates high-quality instruction data without extensive human annotation.

Key Points:

  1. The Problem: Instruction-tuned language models depend heavily on human-written instruction data, which is limited in quantity, diversity, and creativity.

  2. The Solution: SELF-INSTRUCT bootstraps a model’s own capabilities to generate diverse instruction data, including:

    • Task instructions
    • Input-output examples
    • Classification task handling

  3. The Process:

    • Starts with just 175 seed tasks
    • Iteratively prompts the model to generate new instructions
    • Generates corresponding input-output instances
    • Filters invalid or similar instructions
    • Uses the generated data to finetune the original model

  4. Results:

    • Applied to vanilla GPT3, resulting in 52K instructions with 82K instances
    • Demonstrated 33% absolute improvement over original model on SUPER-NATURALINSTRUCTIONS
    • Performance comparable to InstructGPT001, which used private user data and human annotations
    • Only a 5% performance gap behind InstructGPT001 on expert-written novel instructions

  5. Significance: Provides an almost annotation-free method for aligning pretrained language models with instructions, enabling better instruction-following capabilities without expensive human annotation.

This work is particularly important because it addresses a key limitation in scaling instruction-tuned models - the dependency on human-written instruction data. By enabling models to generate their own diverse instruction data, SELF-INSTRUCT offers a path to more general and capable instruction-following AI systems.


PaLM

paper

  • Pathways system
  • Scaled dot product attention
  • Multi-query attention
  • Parallel training techniques

””” Link: https://ai.googleblog.com/2022/04/pathways-language-model-palm-scaling-to.html Family: Transformer Pretraining Architecture: Decoder Pretraining Task: LM Extension: Palm uses a typical decoder-only Transformer architecture, but adds quite a few extensions: SwiGLU activations, parallel layers, multi-query attention, RoPE embeddings, Shared Input-Output Embeddings, no biases, and a 256k SentencePiece vocabulary generated from the training data. Application: PalM is designed as a general purpose language model with applicability to hundreds of different language tasks Date (of first known publication): 04/2022 Num. Params: 540B Corpus: 780B tokens from filtered webpages, books, Wikipedia, news articles, source code, and social media conversations. Code includes 24 programming languages. License: Closed source, Accessible through API Lab: Google “””

Quick Summary

This 2022 paper from Google Research introduces PaLM (Pathways Language Model), a 540-billion parameter autoregressive language model trained on 780 billion tokens of text. The key contributions include:

  1. Efficient scaling: PaLM demonstrates the first large-scale use of Google’s Pathways system, training across 6,144 TPU v4 chips with high efficiency (46.2% model FLOPS utilization).

  2. State-of-the-art performance: PaLM achieves breakthrough performance across a wide range of natural language, reasoning, coding, and multilingual tasks, surpassing prior language models on 28 out of 29 widely-evaluated English NLP benchmarks.

  3. Reasoning capabilities: When combined with chain-of-thought prompting, PaLM shows remarkable capabilities in multi-step reasoning tasks, matching or exceeding the fine-tuned state-of-the-art on various arithmetic and commonsense reasoning benchmarks.

  4. Discontinuous improvements: For certain tasks, scaling from 62B to 540B parameters produced much larger improvements than scaling from 8B to 62B, suggesting emergent capabilities at larger scales.

  5. Thorough analysis: The authors conduct extensive evaluations of memorization, dataset contamination, representational bias, and toxicity, providing a comprehensive understanding of the model’s strengths and limitations.

The paper contributes significantly to understanding how model scaling affects performance and demonstrates that performance improvements from scale had not plateaued as of 2022. The research also establishes a foundation for Pathways as an efficient ML scaling infrastructure at Google.


Gopher (DeepMind)

paper

  • 280B parameter model released in December 2021 DeepMind introduced this model as a “280 billion parameter model” that was “evaluated on 152 diverse tasks, achieving state-of-the-art performance across the majority.”
  • Demonstrated significant scaling benefits in reading comprehension and fact-checking
  • Represented a major advancement in model scale from DeepMind
Quick Summary

This 2021 paper from DeepMind introduces Gopher, a 280 billion parameter autoregressive Transformer language model. The research team trained a family of models ranging from 44 million to 280 billion parameters on a custom dataset called MassiveText (a diverse collection of web pages, books, news articles, and code).

The paper makes several key contributions:

  1. Detailed analysis of how performance scales with model size across 152 diverse tasks, showing that Gopher outperforms previous SOTA on 81% of tasks
  2. Discussion of where scaling works well (knowledge-intensive tasks like fact checking) and where it doesn’t (mathematical and logical reasoning)
  3. Extensive analysis of toxicity and bias in these models, including how these properties change with scale
  4. Exploration of using LLMs in dialogue settings
  5. Analysis of engineering considerations for training at scale, including infrastructure and optimization techniques

The paper provides valuable insights into the capabilities and limitations of large language models circa 2021, predating many subsequent developments in the field but establishing important scaling trends and evaluation methodologies.


Megatron-Turing NLG

paper

  • 530B parameter model announced in October 2021
  • Combined Microsoft’s Turing and NVIDIA’s Megatron technologies
  • Demonstrated advanced distributed training techniques
  • Applied significant hardware optimization for large-scale training
Quick Summary

This paper presents Megatron-Turing NLG (MT-NLG), a 530 billion parameter autoregressive language model developed jointly by Microsoft and NVIDIA. At the time of publication (early 2022), this was the largest monolithic transformer-based language model ever trained. The paper focuses on three main aspects:

  1. Training Infrastructure: The authors detail their 3D parallelism approach, combining data, pipeline, and tensor-slicing parallelism to efficiently train at scale using DeepSpeed and Megatron frameworks.

  2. Training Data and Process: The paper discusses their curated dataset comprising hundreds of billions of tokens, preprocessing techniques, and training recipes that improved optimization efficiency and stability.

  3. Model Evaluation: The authors present extensive evaluation results showing MT-NLG’s superior performance on various NLP benchmarks in zero-shot, one-shot, and few-shot learning settings.

The model demonstrates impressive improvements in natural language understanding and generation capabilities, establishing new state-of-the-art results across several benchmarks. The authors also explore the model’s social biases and in-context learning abilities.


2022: Democratization

EFFICIENTLY SCALING TRANSFORMER INFERENCE

paper

Quick Summary

This 2022 paper from Google researchers addresses the crucial challenge of deploying large language models (LLMs) efficiently for inference. In particular, they focus on:

  1. Partitioning strategies for distributing large models (500B+ parameters) across multiple accelerator chips (TPU v4) that minimize communication costs while maximizing computational efficiency

  2. Memory optimizations, especially utilizing multiquery attention to reduce KV cache memory requirements, enabling 32× longer context lengths

  3. Low-level engineering optimizations including int8 quantization and communication/computation overlap techniques

The authors present an analytical model for selecting optimal partitioning strategies based on application requirements (latency vs. throughput), then empirically validate their approach using the PaLM family of models (8B, 62B, and 540B parameters). Their results demonstrate impressive achievements: 29ms per token latency for generation and 76% model FLOPS utilization (MFU) for processing input with 2048-token context on the PaLM 540B model.

The research provides a clear framework for making partitioning decisions based on model characteristics and deployment requirements, advancing the practical deployment of massive language models.


“”” The primary goal of this paper is to provide a set of engineering principles for how best to partition a model in order to scale Transformer inference. In other words, how is the performance of different partitioning strategies affected by changes in model size, sequence length, and number of hardware chips? How does the optimal partitioning strategy change when trading off between latency and throughput? What is the intuitive and mathematical reasoning behind these effects?

””” https://rasa.com/blog/compressing-bert-for-faster-prediction-2/

Fast Inference from Transformers via Speculative Decoding

paper

Quick Summary

This paper introduces “speculative decoding,” a technique to accelerate inference from large autoregressive Transformer models without changing their architecture, training procedure, or output distribution.

The key insight is that Language Modeling often contains easier subtasks that can be approximated by smaller, more efficient models. The authors use these smaller models to “speculate” on the next few tokens that the larger model would generate, and then run the larger model in parallel to verify these speculations.

When the smaller model’s predictions match what the larger model would have produced, they accept multiple tokens at once, significantly reducing the number of sequential calls to the large model. The authors introduce a novel sampling method called “speculative sampling” that preserves the exact output distribution of the original model.

Their experiments show 2-3x speedups for T5-XXL (11B parameters) without any changes to model outputs, and they analyze various smaller models as approximators, finding that models about two orders of magnitude smaller than the target model provide good trade-offs between accuracy and speed.


Chinchilla

paper While the Chinchilla model itself wasn’t released until 2022, the research behind it began in 2021, establishing important scaling principles that:

  • Showed optimal token-to-parameter ratios should be approximately 20:1 This research found that “we need around 20 text tokens per parameter” for optimal training.
  • Demonstrated many existing models were significantly undertrained
  • Influenced the training methodology of subsequent models

””” Link: https://arxiv.org/abs/2203.15556 Family: GPT Pretraining Architecture: Decoder Pretraining Task: LM Extension: Same as Gopher but with optimizations to reduce model size and therefore training/inference time with equal or superior performance Application: Same as Gopher/GPT3 Date (of first known publication): 03/2022 Num. Params:70B Corpus: Massive Text License: Closed source. Lab: Deepmind “””

Quick Summary

This 2022 paper by DeepMind (Hoffmann et al.) presents a significant finding that challenges previous assumptions about scaling large language models (LLMs).

The authors discover that most large language models at the time (like GPT-3, Gopher, Jurassic-1) were significantly undertrained relative to their size. Through extensive experimentation with over 400 language models of various sizes trained on different amounts of data, they establish a key principle: for compute-optimal training, model size and training tokens should be scaled in equal proportions. This contradicts previous scaling laws from Kaplan et al. (2020), which suggested scaling model size more aggressively than training data.

To validate their findings, they trained “Chinchilla,” a 70B parameter model on 1.4 trillion tokens, using the same compute budget as Gopher (280B parameters on 300B tokens). Chinchilla consistently outperformed much larger models like Gopher, GPT-3, and Megatron-Turing NLG across various benchmarks, achieving a state-of-the-art 67.5% accuracy on the MMLU benchmark.

This work highlights the importance of balanced scaling between model size and training data, and explains why focusing solely on model size isn’t optimal. The paper has been highly influential in shaping how subsequent LLMs were developed.


Chain-of-thought prompting

paper

Quick Summary

This 2022 paper by Jason Wei et al. from Google Research introduces “chain-of-thought prompting,” a simple but powerful technique that enables large language models to perform complex reasoning tasks. The key insight is that by providing examples where the model sees step-by-step reasoning before giving an answer, the model learns to generate its own reasoning chains for new problems.

The authors demonstrate that this ability emerges naturally in sufficiently large language models (like PaLM 540B) without any fine-tuning. The technique significantly improves performance on arithmetic, commonsense, and symbolic reasoning tasks. On some benchmarks like GSM8K (math word problems), the approach achieves state-of-the-art results, outperforming even fine-tuned models.

What’s particularly interesting is that this reasoning ability is “emergent” - it only appears in models above a certain size threshold, and smaller models actually perform worse with chain-of-thought prompting than with standard prompting.


InstructGPT

paper

https://openai.com/index/instruction-following/

””” Link: https://github.com/openai/following-instructions-human-feedback Family: GPT Pretraining Architecture: Decoder Pretraining Task: LM Extension: GPTInstruct starts off with a pretrained GPT3 model and adds reward modeling through reinforcement learning after a supervised finetuning Application: Knowledge-intensive dialog or language tasks Date (of first known publication): 01/2022 Num. Params: Same as GPT3 Corpus: Same as GPT3 for pretraining, but finetuned and optimized using labeler data and prompts License: Closed source, Accessible through API Lab: OpenAI “””

Quick Summary

This paper introduces InstructGPT, a model trained to follow human instructions by fine-tuning GPT-3 using reinforcement learning from human feedback (RLHF). The authors show that alignment with human preferences can be achieved through a three-step process:

  1. Collecting human demonstrations of desired behavior for supervised fine-tuning (SFT)
  2. Gathering human comparisons between model outputs to train a reward model
  3. Using reinforcement learning to optimize the model against this reward function

Their key findings show that even smaller InstructGPT models (1.3B parameters) can outperform the much larger GPT-3 (175B parameters) in terms of following user instructions, truthfulness, and harmlessness - demonstrating that alignment doesn’t necessarily require larger models. The approach also reduces harmful outputs while maintaining good performance on standard NLP benchmarks with minimal regressions.

This work is significant as it provides a practical approach to aligning language models with human intent, though the authors note limitations including the model still making simple mistakes and the alignment being specifically to their team of human labelers rather than broader human values.


BLOOM

paper

  • Multilingual pre-training
  • Carbon footprint considerations
  • Distributed training
  • Community governance

””” Link: https://huggingface.co/docs/transformers/model_doc/bloom Family: GPT Pretraining Architecture: Decoder Pretraining Task: LM Extension: Main difference to GPT-3 is that it uses full attention instead of sparse attention Application: Same as GPT-3 Date (of first known publication): 07/2022 Num. Params:176B Corpus: 366B tokens (1.5 TB of text data) multilingual dataset Lab: Big Science/Huggingface License: Open, but need to follow restrictions in Attachment A, BigScience RAIL License v1.0 “””

Quick Summary

This paper introduces BLOOM (BigScience Large Open-science Open-access Multilingual Language Model), a 176 billion parameter language model created through a large-scale collaborative effort called BigScience. Here’s a high-level summary:

Key Points:

  1. Open and Collaborative: Unlike many large language models developed by well-resourced organizations, BLOOM was created through a collaboration of hundreds of researchers and is publicly released.

  2. Multilingual Focus: BLOOM was trained on 46 natural languages and 13 programming languages, addressing the English-centric bias of many previous large language models.

  3. Training Data: The model was trained on the ROOTS corpus, a carefully curated 1.61TB dataset spanning multiple languages, with attention to data governance and ethical considerations.

  4. Architecture: BLOOM uses a causal decoder-only Transformer architecture with 176B parameters, incorporating ALiBi positional embeddings and embedding layer normalization.

  5. Evaluation: The model shows competitive performance on various benchmarks, including SuperGLUE, machine translation, summarization, and code generation. Performance improves significantly after multitask prompted finetuning (resulting in BLOOMZ).

  6. Environmental Impact: The authors estimate BLOOM’s carbon footprint at 25 tons of CO2eq, significantly less than models like GPT-3 (502 tons), partly due to using a low-carbon energy grid.

  7. Ethical Considerations: The paper discusses social limitations of LLM development and how the BigScience effort tried to address these through an Ethical Charter, more diverse representation, and a Responsible AI License.

This paper represents a significant milestone in democratizing access to large language model technology while also attempting to address some of the ethical, environmental, and linguistic diversity concerns associated with these powerful systems.

Is there a specific aspect of the paper you’d like to explore further?


Emergent Abilities of Large Language Models

paper

Quick Summary

This paper by researchers from Google, Stanford, UNC Chapel Hill, and DeepMind explores a fascinating phenomenon they call “emergent abilities” in large language models (LLMs).

The key idea is that some capabilities in LLMs do not appear gradually as models scale up, but rather emerge suddenly when models reach a certain size threshold. Before this threshold, models perform at random chance on certain tasks, but after crossing this threshold, performance jumps significantly. This pattern differs from the smooth, predictable scaling laws typically observed in language model pretraining.

The paper defines emergent abilities as “abilities that are not present in smaller models but are present in larger models,” meaning they cannot be predicted by simply extrapolating performance improvements from smaller models.

Some examples they document include:

  • Arithmetic reasoning with 3-digit numbers
  • Translation from phonetic alphabets
  • Word unscrambling
  • Various types of reasoning tasks

The authors also explore how certain capabilities like chain-of-thought reasoning, instruction following, and self-consistency only emerge at certain model scales and may be harmful for smaller models.

The paper raises important questions about what other abilities might emerge with further scaling, whether emergence thresholds could be lowered with better architectures or training data, and why emergence happens at all.


Flash Attention

paper

Quick Summary

This paper introduces FlashAttention, an algorithm that makes the standard Transformer attention mechanism significantly faster and more memory-efficient by being “IO-aware” - that is, by carefully managing how data moves between different levels of GPU memory (high-bandwidth memory and on-chip SRAM).

The key innovations are:

  1. Using tiling techniques to avoid materializing the large N×N attention matrix in GPU high-bandwidth memory
  2. Recomputing certain values during the backward pass rather than storing them
  3. Fusing multiple operations into a single GPU kernel to minimize memory traffic

These techniques reduce memory requirements from quadratic to linear in sequence length and achieve substantial speedups (3-7.6x on attention computation). This enables training Transformers with much longer context lengths, leading to better model quality and new capabilities like solving the Path-X sequence modeling challenge (16K tokens).

The authors also extend FlashAttention to block-sparse attention, creating an even faster approximate attention algorithm.


Grouped-query attention

paper

Quick Summary

This paper from Google Research tackles an important problem in transformer model inference: the memory bandwidth bottleneck caused by loading keys and values during autoregressive decoding.

The authors make two main contributions:

  1. Uptraining Existing Models: They show that existing multi-head attention (MHA) models can be efficiently converted to multi-query attention (MQA) models using just 5% of the original pre-training compute. Rather than training new models from scratch for faster inference, this approach allows reusing existing checkpoints.

  2. Introducing Grouped-Query Attention (GQA): They propose a new attention mechanism that sits between MHA (where every query has its own key and value head) and MQA (where all queries share a single key-value head). GQA organizes query heads into groups, with each group sharing a key-value head.

The results demonstrate that GQA achieves quality close to multi-head attention while being nearly as fast as multi-query attention - essentially getting the best of both worlds. This approach is particularly beneficial for larger models where the memory bandwidth from loading the KV cache becomes a major bottleneck.

I’d be happy to dive deeper into any specific aspect of the paper that interests you most.


ALiBi position encoding

paper

Quick Summary

This paper introduces ALiBi (Attention with Linear Biases), a position encoding method for transformer models that enables training on shorter sequences while extrapolating to longer sequences at inference time.

The key contributions are:

  1. The authors identify a limitation in transformers: models trained on sequences of length L struggle to handle longer sequences at inference time.

  2. They show that existing position encoding methods (sinusoidal, rotary, T5 bias) have limited extrapolation capabilities.

  3. They introduce ALiBi, which doesn’t add positional embeddings but instead modifies attention by applying a distance-based linear bias to attention scores.

  4. ALiBi enables models to be trained on shorter sequences and extrapolate effectively to much longer ones - even extrapolating to sequences that are 2-10x longer than those seen during training.

  5. The method is computationally efficient and requires minimal changes to transformer code, with no additional parameters.

  6. Experiments show ALiBi outperforms other position methods on WikiText-103 and other datasets, even when extrapolating.

This work has significant practical implications for transformer efficiency, as training on shorter sequences requires substantially less computational resources while still enabling effective processing of longer sequences during inference.


DeepSpeed Inference: Enabling Efficient Inference of Transformer Models at Unprecedented Scale

paper

Quick Summary

This paper introduces DeepSpeed Inference, a comprehensive system for efficient inference of transformer models at unprecedented scales. The authors address challenges in deploying extremely large transformer models (from billions to trillions of parameters) for inference applications.

The main components of DeepSpeed Inference include:

  1. DeepSpeed Transformer: A GPU-only solution designed to minimize latency while maximizing throughput for both dense and sparse transformer models. It includes optimized single-GPU transformer kernels, many-GPU dense transformer layer, and massive-GPU scale sparse transformer layer.

  2. ZeRO-Inference: A heterogeneous solution that leverages CPU and NVMe memory in addition to GPU memory to enable high inference throughput with large models that don’t fit in aggregate GPU memory.

Their results demonstrate significant improvements:

  • Reduces latency by up to 7.3× over state-of-the-art for latency-oriented scenarios
  • Increases throughput by over 1.5x for throughput-oriented scenarios
  • Enables trillion-parameter scale inference under real-time latency constraints
  • Can inference 25× larger models than GPU-only solutions while delivering high throughput

The paper addresses specific challenges in transformer inference related to memory bandwidth, throughput, and resource constraints, providing a comprehensive solution for the increasingly diverse landscape of transformer models.


Claude 1

  • Initial release focusing on helpfulness and harmlessness

FLAN (Fine-tuned LAnguage Net) (Google)

paper

  • Instruction tuning across multiple tasks
  • Improved zero-shot performance
Quick Summary

This 2022 ICLR paper by Jason Wei and colleagues at Google Research introduces “instruction tuning” - a simple yet effective approach to improve zero-shot learning capabilities of large language models. The authors:

  1. Take a 137B parameter pretrained language model
  2. Finetune it on 60+ NLP datasets that are described via natural language instructions
  3. Call this instruction-tuned model “FLAN” (Finetuned Language Net)
  4. Evaluate FLAN on unseen task types using a careful methodology

The key findings are impressive:

  • FLAN significantly outperforms zero-shot performance of the base model
  • FLAN surpasses GPT-3’s zero-shot performance on 20 of 25 datasets evaluated
  • FLAN even outperforms few-shot GPT-3 on several datasets (ANLI, RTE, BoolQ, etc.)

Through ablation studies, they identify three critical factors for successful instruction tuning:

  • Number of finetuning datasets (more is better)
  • Model scale (benefits only emerge at sufficient scale)
  • Natural language instructions (essential for cross-task transfer)

This paper represents an important step in making large language models more capable of following natural language instructions without examples, expanding their practical utility for a wider audience.


Red Teaming Language Models with Language Models

paper

Quick Summary

This paper by Perez et al. introduces a novel approach for identifying harmful behaviors in language models (LMs) using other language models as “red team” attackers. Rather than relying on human-written test cases, which can be expensive and limited in scope, they demonstrate how to automatically generate test cases that effectively expose weaknesses in target LMs.

The researchers show that their method can uncover a variety of harms in a 280B parameter chatbot, including:

  • Offensive language generation
  • Leakage of private training data
  • Generation of inappropriate contact information
  • Distributional biases against certain groups
  • Escalating harmful behaviors in multi-turn dialogues

The paper provides a significant methodological contribution by exploring several techniques for generating test cases, from zero-shot generation to reinforcement learning, and demonstrates that LM-based red teaming can complement manual testing approaches.


HELM (Holistic Evaluation of Language Models)

paper

[its 170 pages, I am not reading it]

Comprehensive benchmark suite for LLMs Standardized evaluation metrics

Quick Summary


DALL-E 2 (OpenAI)

  • Released in April 2022
  • Significant improvement over original DALL-E
  • Demonstrated remarkably detailed text-to-image generation
  • Maintained controlled access with gradual rollout

Stable Diffusion (Stability AI)

  • Released in August 2022 as “a deep learning, text-to-image model” that became “the premier product of Stability AI”
  • Open-source alternative to DALL-E 2
  • Democratized access to high-quality image generation
  • Trained on LAION-5B dataset

GPTQ

paper

[also add how multi gpu inference works]

Quick Summary

This paper addresses the challenge of compressing large language models (LLMs) like GPT-3 and BLOOM for more efficient inference. The key contribution is GPTQ, a novel one-shot weight quantization method that can compress models with billions of parameters down to 3-4 bits per weight with minimal accuracy loss.

At a high level:

  • GPTQ builds on previous work in post-training quantization, specifically adapting the Optimal Brain Quantization approach
  • It introduces key optimizations that make quantization feasible for models with 175B+ parameters
  • The method enables quantizing these massive models in just a few hours on a single GPU
  • Results show GPTQ can maintain model performance while more than doubling compression compared to prior methods
  • The authors demonstrate running a 175B parameter model on a single GPU for the first time

The practical impact is significant: GPTQ allows large models to run with far fewer computational resources, achieving 3.25x speedups on high-end GPUs and 4.5x speedups on more cost-effective ones, making these powerful models more accessible to researchers and practitioners.


Beyond the Imitation Game: Quantifying and extrapolating the capabilities of language models

paper

[BIG-Bench benchmark, 95 pages of benchmark ahhhhhhhh]

Quick Summary


Minerva

paper

Quick Summary

This paper introduces Minerva, a large language model specifically designed to solve quantitative reasoning problems in mathematics and science. The key innovation is training PaLM models (8B, 62B, and 540B parameters) on a carefully curated dataset of mathematical content from arXiv papers and web pages containing LaTeX formatting.

Main Contributions:

  • Dataset: 38.5B tokens of mathematical content that preserves LaTeX notation and mathematical expressions
  • Performance: Achieves state-of-the-art results on MATH dataset (50.3% with majority voting vs. previous 6.9%), GSM8k (78.5%), and MMLU-STEM (75.0%)
  • Evaluation: Introduces OCWCourses dataset with 272 undergraduate-level STEM problems
  • Method: Uses majority voting over multiple samples rather than external tools or calculators

Key Insight: By training on mathematically rich text that preserves formal notation (rather than just natural language descriptions of math), the model learns to manipulate mathematical symbols and follow step-by-step reasoning patterns effectively.

The paper demonstrates that language models can achieve impressive mathematical reasoning capabilities when trained on appropriate data, though they still fall short of human expert performance and have notable limitations in verification and complex multi-step problems.


ChatGPT

The beginning of an Era

2023: Multi-Modal and Reasoning

Efficient Memory Management for Large Language Model Serving with PagedAttention

paper

Quick Summary

This paper introduces “PagedAttention,” a novel attention algorithm for efficiently serving Large Language Models (LLMs), and “vLLM,” a system built on this algorithm. The key innovation is inspired by virtual memory and paging techniques from operating systems - they divide the key-value (KV) cache memory into fixed-size blocks that can be stored non-contiguously, rather than requiring contiguous memory allocation.

The KV cache is a significant memory bottleneck in LLM serving, often consuming around 30% of GPU memory. Traditional systems like FasterTransformer and Orca suffer from both internal and external memory fragmentation because they allocate contiguous memory chunks based on maximum possible sequence length, resulting in significant memory waste.

PagedAttention significantly improves memory efficiency by:

  1. Reducing fragmentation through block-level memory management
  2. Enabling flexible sharing of KV cache within and across requests
  3. Supporting dynamic memory allocation as sequences grow

Their experiments show vLLM improves throughput by 2-4× compared to state-of-the-art systems while maintaining the same latency, with even greater improvements for longer sequences, larger models, and complex decoding algorithms like beam search.


QLoRA: Efficient Finetuning of Quantized LLMs

paper

Quick Summary

This paper introduces QLORA (Quantized Low-Rank Adaptation), a significant advancement in efficient fine-tuning of large language models (LLMs). The key innovation is allowing 4-bit quantized models to be fine-tuned without performance degradation compared to full 16-bit precision models.

The main contributions include:

  1. 4-bit NormalFloat (NF4): A new data type optimized for normally distributed weights
  2. Double Quantization: A technique to reduce memory footprint by quantizing the quantization constants
  3. Paged Optimizers: A method to manage memory spikes during training

These innovations collectively allow fine-tuning of a 65B parameter model on a single 48GB GPU while maintaining full 16-bit fine-tuning performance. This represents a dramatic improvement in accessibility, reducing the memory requirements from over 780GB to under 48GB.

The authors demonstrate QLORA’s effectiveness by developing Guanaco, a family of models fine-tuned on the OASST1 dataset that performs competitively with ChatGPT on benchmark tests while requiring only 24 hours of training on a single GPU.


Parameter-Efficient Fine-Tuning Methods for Pretrained Language Models: A Critical Review and Assessment

paper

https://huggingface.co/blog/diffusers-quantization

Quick Summary

This paper provides a comprehensive review and assessment of Parameter-Efficient Fine-Tuning (PEFT) methods for pretrained language models (PLMs). The authors address an important challenge in modern NLP: as language models grow increasingly larger (from BERT’s 110M parameters to Falcon’s 180B parameters), traditional fine-tuning becomes computationally prohibitive for many practitioners.

The paper categorizes PEFT methods into five main types:

  1. Additive fine-tuning (adding new parameters)
  2. Partial fine-tuning (updating only a subset of original parameters)
  3. Reparameterized fine-tuning (using low-rank decomposition)
  4. Hybrid fine-tuning (combining different PEFT approaches)
  5. Unified fine-tuning (proposing a unified framework)

The authors conduct experiments with 11 representative PEFT methods across various NLP tasks to evaluate parameter efficiency and memory usage. Their analysis shows that most PEFT methods significantly reduce trainable parameters while maintaining performance comparable to full fine-tuning, with some methods even outperforming it.

The paper also discusses applications of PEFT methods in multi-task learning, cross-lingual transfer, and backdoor attack/defense, concluding with future research directions in this rapidly evolving field.


FlashAttention-2: Faster Attention with Better Parallelism and Work Partitioning

paper

Quick Summary

This paper presents FlashAttention-2, an improved algorithm for implementing attention mechanisms in Transformer models that significantly enhances computational efficiency. Building on the original FlashAttention work, FlashAttention-2 introduces better parallelism and work partitioning strategies that achieve approximately 2× speedup over its predecessor.

The key innovations include:

  1. Algorithm optimizations to reduce non-matrix multiplication operations
  2. Improved parallelization across sequence length dimensions
  3. Better work distribution between GPU thread blocks and warps to minimize communication overhead

The results are impressive - reaching 50-73% of theoretical maximum FLOPs/s on A100 GPUs and achieving up to 225 TFLOPs/s when used in end-to-end GPT model training (72% model FLOPs utilization).

This advancement directly addresses the challenge of scaling Transformers to longer sequence lengths, which is critical for applications like processing long documents, high-resolution images, and video data.


AWQ: Activation-aware Weight Quantization for LLM Compression and Acceleration

paper

Quick Summary

This paper addresses the challenge of deploying large language models (LLMs) directly on edge devices, which is important for privacy, offline usage, and reduced operational costs. The authors propose Activation-aware Weight Quantization (AWQ), a hardware-friendly approach for low-bit weight-only quantization of LLMs.

Key contributions:

  1. The observation that not all weights in an LLM are equally important - protecting just 1% of salient weights can greatly reduce quantization error
  2. The insight that salient weight channels should be identified based on activation distribution rather than weight values
  3. A mathematical derivation showing that scaling up salient channels can reduce quantization error without using mixed-precision
  4. Implementation of TinyChat, an efficient inference framework for 4-bit LLMs on edge devices

Their method demonstrates superior performance over existing quantization approaches across various language model benchmarks, including instruction-tuned LMs and multi-modal LMs. The TinyChat implementation achieves more than 3× speedup over Huggingface FP16 implementations on both desktop and mobile GPUs, enabling even 70B parameter models to run on mobile GPUs.


Generative Agents: Interactive Simulacra of Human Behavior

Now we have started to get into the region of AI agents. I will recommend checking my blog on the topic for a beginner friendly introduction to the topic.

paper

Quick Summary

This paper introduces “generative agents” - computational agents powered by large language models that simulate believable human behavior in interactive environments. The authors present an architecture that extends language models to:

  1. Store comprehensive records of agents’ experiences using natural language
  2. Synthesize memories into higher-level reflections
  3. Retrieve relevant information dynamically to plan behavior

The paper demonstrates this approach by creating a small town populated with 25 agents in a sandbox environment inspired by The Sims. These agents exhibit both individual behaviors (waking up, cooking, working) and emergent social dynamics (spreading information, forming relationships, coordinating activities).

A key example highlighted is how, from a single prompt about one agent wanting to throw a Valentine’s Day party, the agents autonomously spread invitations, form new acquaintances, coordinate attendance, and even arrange dates to the party.

The authors evaluate their system through controlled experiments and an end-to-end simulation, showing that their architecture components (observation, planning, and reflection) each contribute significantly to the believability of agent behavior.

This work represents an interesting intersection of large language models, interactive systems, and human behavior simulation with potential applications in virtual environments, social prototyping, and training scenarios.


Voyager: An Open-Ended Embodied Agent with Large Language Models

paper

Quick Summary

This paper introduces VOYAGER, a novel AI agent that uses Large Language Models (specifically GPT-4) to enable lifelong learning and exploration in the open-world environment of Minecraft without human intervention.

The key innovations of VOYAGER include:

  1. Automatic Curriculum: A self-driven goal-setting system that proposes appropriate tasks based on the agent’s current skills and environment state, maximizing exploration.

  2. Skill Library: A repository of executable code for storing and retrieving complex behaviors, allowing the agent to build increasingly sophisticated skills over time.

  3. Iterative Prompting Mechanism: A system that incorporates environment feedback, execution errors, and self-verification to improve program generation.

VOYAGER outperforms previous state-of-the-art approaches by obtaining 3.3× more unique items, traveling 2.3× longer distances, and unlocking key tech tree milestones up to 15.3× faster. It can also transfer learned skills to new Minecraft worlds to solve novel tasks, demonstrating strong generalization capabilities.

The approach is particularly interesting because it creates a lifelong learning agent that operates through code generation rather than traditional reinforcement learning methods, with no need for model parameter fine-tuning.


Universal and Transferable Adversarial Attacks on Aligned Language Models

paper

Quick Summary

This 2023 paper by Zou et al. demonstrates a concerning vulnerability in aligned language models (LLMs) such as GPT, Claude, and others that have been fine-tuned not to produce harmful content. The researchers develop a surprisingly effective method called “Greedy Coordinate Gradient” (GCG) to generate adversarial prompts that can reliably make these models generate harmful, objectionable content despite their alignment training.

The key findings include:

  1. The researchers can automatically generate adversarial suffixes that, when attached to harmful prompts, convince LLMs to respond affirmatively rather than refusing
  2. These attacks transfer remarkably well between models - suffixes trained on smaller open-source models like Vicuna work effectively against commercial models like GPT-3.5, GPT-4, and to a lesser extent Claude
  3. The attack success rates are quite high - up to 88% on the models they directly targeted, and as high as 84% transfer success rate to commercial models
  4. The method significantly outperforms previous approaches for automated adversarial prompting

This represents a significant advancement in understanding vulnerabilities in LLM safety measures and raises important questions about current alignment techniques.

I’m ready to explore any specific aspects of this paper that interest you, from the mathematical formulation of their attack method to the implications for language model safety.


Tree of Thoughts: Deliberate Problem Solving with Large Language Models

paper

Quick Summary

This paper introduces “Tree of Thoughts” (ToT), a framework that enhances large language models’ (LLMs) problem-solving abilities by enabling more deliberate reasoning and exploration. Unlike standard autoregressive text generation or even Chain of Thought prompting, ToT allows LLMs to:

  1. Generate multiple intermediate “thoughts” (coherent text units that represent steps toward a solution)
  2. Evaluate these thoughts using the model’s own reasoning capabilities
  3. Explore different reasoning paths systematically using search algorithms (breadth-first or depth-first search)
  4. Use backtracking and lookahead to make more global decisions

The authors demonstrate significant improvements on three challenging tasks:

  • Game of 24 (mathematical reasoning): ToT achieved 74% success vs. 4% for GPT-4 with chain-of-thought
  • Creative Writing (coherent multi-paragraph construction)
  • Mini Crosswords (constraint satisfaction with linguistic knowledge)

This framework represents an interesting bridge between classical AI problem-solving methods (tree search) and modern LLMs, adding a more deliberate “System 2” thinking process to complement the associative “System 1” capabilities of LLMs.


Mpt

blog

Quick Summary

MosaicML introduced MPT-7B (MosaicML Pretrained Transformer), a 7 billion parameter language model that addresses key limitations in open-source LLMs. The model’s key features include:

  1. Commercial usability - Licensed under Apache-2.0, unlike models like LLaMA
  2. Extensive training - Trained on 1 trillion tokens of text and code
  3. Long context handling - Can process inputs up to 65k tokens (and even 84k in some cases) thanks to ALiBi
  4. Optimized performance - Uses FlashAttention and FasterTransformer for improved training and inference
  5. Competitive quality - Matches LLaMA-7B on standard benchmarks

They released four variants:

  • MPT-7B Base (general foundation model)
  • MPT-7B-StoryWriter-65k+ (for long-form creative writing)
  • MPT-7B-Instruct (for instruction following)
  • MPT-7B-Chat (for conversational interactions)

The model was trained in 9.5 days on 440 A100 GPUs at a cost of around $200,000, with zero human intervention required during training.


WizardLM: Empowering Large Language Models to Follow Complex Instructions

paper

Quick Summary

This paper introduces “Evol-Instruct,” a novel method for automatically generating complex instruction data to improve large language models’ (LLMs) instruction-following capabilities. Rather than relying on expensive and time-consuming human annotation of complex instructions, the authors propose using LLMs themselves to evolve simple instructions into more complex ones through systematic operations.

The key contributions include:

  1. An evolutionary approach to instruction generation that can produce increasingly complex instructions through “In-depth Evolving” (making instructions more complex) and “In-breadth Evolving” (creating diverse new instructions)

  2. WizardLM, a model created by fine-tuning LLaMA with these evolved instructions that shows impressive performance compared to other instruction-tuned models

  3. Evidence that AI-generated complex instructions can be superior to human-created ones for training LLMs, especially for handling complex queries

Their experiments show that WizardLM outperforms models like Alpaca and Vicuna on various benchmarks, and even outperforms ChatGPT on high-complexity tasks according to human evaluations.

Is there a specific aspect of the paper you’d like to explore further? I’m happy to delve into the Evol-Instruct methodology, the evaluation approach, the mathematical components, or any other elements you find interesting.


DeepSpeed-Chat: Easy, Fast and Affordable RLHF Training of ChatGPT-like Models at All Scales

paper

Quick Summary

This 2023 paper from Microsoft’s DeepSpeed team introduces DeepSpeed-Chat, a system designed to democratize the training of ChatGPT-like models using Reinforcement Learning from Human Feedback (RLHF). The system addresses three key challenges in the current landscape: accessibility, efficiency, and affordability of RLHF training, particularly for models with billions of parameters.

DeepSpeed-Chat offers three main capabilities:

  1. An easy-to-use training and inference experience for ChatGPT-like models
  2. A DeepSpeed-RLHF pipeline that replicates the three-step training pipeline from InstructGPT (supervised fine-tuning, reward model training, and RLHF)
  3. A unified “Hybrid Engine” that optimizes both training and inference phases

The paper demonstrates impressive efficiency gains - up to 15x faster than existing systems - making RLHF training both faster and more affordable. For example, they show training an OPT-13B model in just 9 hours for about $290 on Azure, and scaling to train a 175B parameter model in under a day. The system also enables training of much larger models on limited hardware, such as running a 13B parameter model on a single GPU.


GPT-4

paper

  • Multi-modal encoders
  • System prompting
  • Advanced reasoning capabilities
  • Tool use
Quick Summary


Mistral 7b

paper

Quick Summary

This paper introduces Mistral 7B, a 7-billion-parameter language model that achieves impressive efficiency and performance. The authors demonstrate that Mistral 7B outperforms larger models like Llama 2 (13B) across all benchmarks tested, and even surpasses Llama 1 (34B) in reasoning, mathematics, and code generation domains.

The key architectural innovations include:

  1. Grouped-query attention (GQA) for faster inference and reduced memory requirements
  2. Sliding window attention (SWA) to handle arbitrary sequence lengths with lower computational costs
  3. A rolling buffer cache mechanism to maintain efficiency with long sequences

The paper also presents Mistral 7B-Instruct, a fine-tuned version that outperforms Llama 2 13B-chat on both human and automated benchmarks. All models are released under the Apache 2.0 license.

This work challenges conventional scaling laws by showing that careful architecture design can achieve better performance with fewer parameters, suggesting new directions for efficient LLM development.


LLaMA

paper

  • Efficient scaling
  • Flash Attention-2
  • Chat templates
  • RLHF improvements

””” Link: https://huggingface.co/docs/transformers/main/model_doc/llama Family: Transformer Pretraining Architecture: Decoder Pretraining Task: LM Extension: LLaMA uses a Transformer architecture, and with extensions: Pre-normalization, SwiGLU activations, RoPE embeddings, reduced memory usage and runtime through efficient implementation of the causal multi-head attention, checkpointing to reduce the amount of activations that are recomputed during the backward pass, model and sequence parallelism to reduce memory usage of the model, and uses 1.4T BPE tokens after tokenization. Application: Zero and few shot Commonsense reasoning, Question answering, Code generation and Reading comprehension. Date (of first known publication): 02/2023 Num. Params: 7B, 13B, 33B and 65B Corpus: English CommonCrawl + C4 + Github + Wikipedia + Gutenberg and Books3 + ArXiv + Stack Exchange License: Limited, Non-commercial bespoke license Lab: Meta “””

Quick Summary

This paper from Meta AI introduces LLaMA, a collection of foundation language models ranging from 7B to 65B parameters. The key contributions include:

  1. Creating state-of-the-art models trained exclusively on publicly available datasets (unlike many competitors that use proprietary data)
  2. Demonstrating that smaller models trained on more tokens can outperform larger models (e.g., LLaMA-13B outperforms GPT-3 175B on most benchmarks)
  3. Making these models available to the research community

The researchers focus on optimizing for inference efficiency rather than just training efficiency. They train their models on trillions of tokens (more than typically used) and implement architectural improvements including pre-normalization, SwiGLU activation functions, and rotary positional embeddings.

The paper also examines performance across various benchmarks including common sense reasoning, question answering, reading comprehension, mathematical reasoning, and code generation.


Mixtral 8x7B

paper

Quick Summary

This paper from Mistral AI introduces Mixtral 8x7B, a Sparse Mixture of Experts (SMoE) language model that represents a significant advancement in efficient language model architecture. Let me provide a concise overview of the key contributions:

The Mixtral 8x7B model:

  • Builds on the Mistral 7B architecture but replaces the feedforward blocks with Mixture-of-Experts (MoE) layers
  • Contains 8 expert networks per layer, with each token dynamically routed to 2 experts
  • Has 47B total parameters but only activates 13B parameters per token (improving efficiency)
  • Trained with a 32k token context window on multilingual data
  • Outperforms Llama 2 70B and GPT-3.5 on most benchmarks despite using fewer active parameters
  • Shows particular strength in mathematics, code generation, and multilingual tasks
  • Available in both a base version and an instruction-tuned version (Mixtral 8x7B - Instruct)
  • Released under the Apache 2.0 license for both academic and commercial use

The instruction-tuned version (Mixtral 8x7B - Instruct) performs exceptionally well, surpassing GPT-3.5 Turbo, Claude-2.1, Gemini Pro, and Llama 2 70B chat models on human evaluation benchmarks.


LLaMA 2

https://yeokhengmeng.com/2025/04/llama2-llm-on-dos/

paper

Quick Summary

This paper introduces Llama 2, Meta’s updated collection of large language models (LLMs) ranging from 7 billion to 70 billion parameters. The paper focuses on two main offerings:

  1. Llama 2 - Base pretrained models that improve upon Llama 1 with more training data (2 trillion tokens), longer context length (4096 tokens), and architectural improvements.

  2. Llama 2-Chat - Fine-tuned versions optimized specifically for dialogue applications, using supervised fine-tuning (SFT) and reinforcement learning from human feedback (RLHF).

The authors detail their comprehensive approach to safety alignment and provide extensive evaluation metrics showing that Llama 2-Chat models outperform most open-source alternatives and are competitive with some proprietary models like ChatGPT on helpfulness and safety benchmarks.

Key contributions include detailed methodologies for the fine-tuning process, safety mechanisms, and a transparent discussion of potential limitations and ethical considerations. The models have been released for both commercial and research use.


Vicuna (LMSYS)

paper

  • Fine-tuned LLaMA
  • Open-source conversational agent
Quick Summary

This blog post introduces Vicuna-13B, an open-source chatbot developed by fine-tuning Meta’s LLaMA model on approximately 70,000 user-shared conversations collected from ShareGPT. According to their preliminary evaluation using GPT-4 as a judge, Vicuna-13B achieves more than 90% of the quality of OpenAI’s ChatGPT and Google’s Bard while outperforming other open-source models like base LLaMA and Stanford Alpaca in over 90% of test cases.

Key highlights:

  1. Training approach: Fine-tuned LLaMA on user-shared conversations from ShareGPT with improved handling of multi-turn conversations and longer sequences

  2. Cost-efficiency: Training cost was approximately $300 for the 13B model

  3. Novel evaluation method: Used GPT-4 as a judge to evaluate response quality compared to other chatbots

  4. Performance: Achieved competitive results against proprietary models while significantly outperforming other open-source alternatives

  5. Availability: Code, weights, and an online demo released for non-commercial use

The authors acknowledge limitations in mathematical reasoning, factual accuracy, and safety, noting that this represents an open starting point for future research.


Alpaca

paper

  • Efficient fine-tuning approach
  • Instruction-tuned LLaMA “”” Link: https://github.com/tatsu-lab/stanford_alpaca Family: LLaMA Pretraining Architecture: Decoder Fine-tuning Task: human instructions Extension: Alpaca is fine-tuned from a 7B LLaMA model. Application: Evaluated on a variety of text generation and classification tasks. Date (of first known publication): 03/2023 Num. Params: 7B Corpus: 52K instruction-following data generated using self-instruct mechanism, from 175 human-written instruction-output pairs. License: Limited, Non-commercial bespoke license Lab: Stanford “””
Quick Summary

This blog post introduces Alpaca 7B, a model fine-tuned from Meta’s LLaMA 7B using 52,000 instruction-following demonstrations. Stanford researchers created Alpaca to provide the academic community with an accessible instruction-following model comparable to OpenAI’s text-davinci-003, but at a fraction of the cost (under $600 to reproduce).

Key highlights:

  1. Training approach: Used the “self-instruct” method, starting with 175 human-written instruction-output pairs and prompting text-davinci-003 to generate additional examples, resulting in 52K unique instructions

  2. Cost efficiency: Data generation cost less than $500 using OpenAI’s API, and fine-tuning took 3 hours on 8 A100 GPUs (under $100)

  3. Performance: In preliminary human evaluation, Alpaca matched text-davinci-003 performance (winning 90 vs 89 comparisons in pairwise evaluation)

  4. Academic focus: Explicitly designed for academic research only - commercial use prohibited due to LLaMA’s license and OpenAI’s terms of use

  5. Known limitations: Exhibits hallucination, toxicity, and can generate misinformation (authors provide specific examples)

  6. Safety measures: Implemented content filtering via OpenAI’s moderation API and watermarking for the demo

The work aimed to democratize access to instruction-following models for academic research while acknowledging the risks and implementing appropriate safeguards.


Direct Preference Optimization (DPO)

paper

Quick Summary

This paper introduces Direct Preference Optimization (DPO), a revolutionary approach that eliminates the need for reinforcement learning in training language models from human preferences, making the process dramatically simpler while maintaining or improving performance.

Core Innovation: Bypassing Reinforcement Learning

The Problem with RLHF: Traditional Reinforcement Learning from Human Feedback (RLHF) is complex and unstable, requiring:

  1. Training a reward model on preference data
  2. Using RL algorithms (like PPO) to optimize the language model
  3. Careful hyperparameter tuning and sampling during training

DPO’s Breakthrough: The paper shows that this two-stage process can be replaced with a single, simple classification loss that directly optimizes the language model on preference data.

Key Mathematical Insight

The central theoretical contribution is recognizing that your language model is secretly a reward model. Specifically:

  • Standard approach: Learn reward function r(x,y), then use RL to find optimal policy π*
  • DPO insight: Any reward function can be reparameterized as r(x,y) = β log π(y x)/π_ref(y x) + β log Z(x)
  • Key observation: In the Bradley-Terry preference model, the partition function Z(x) cancels out when comparing preferences
  • Result: You can directly optimize the policy using a simple binary cross-entropy loss

The DPO Algorithm

Instead of optimizing a complex RL objective, DPO uses:

L_DPO = -E[(x,y_w,y_l)~D] log σ(β log π_θ(y_w|x)/π_ref(y_w|x) - β log π_θ(y_l|x)/π_ref(y_l|x))

Where:

  • σ is the sigmoid function
  • y_w and y_l are preferred and dispreferred completions
  • β controls the KL penalty strength
  • π_ref is the reference model (typically the SFT model)

Experimental Results

Performance: DPO matches or exceeds PPO-based RLHF across three tasks:

  • Sentiment control: Better reward/KL trade-off than PPO
  • Summarization: 61% win rate vs PPO’s 57% on TL;DR dataset
  • Dialogue: Only method to improve over baseline on Anthropic-HH dataset

Simplicity: Eliminates the need for:

  • Reward model training
  • RL optimization loops
  • Sampling during training
  • Extensive hyperparameter tuning

Theoretical Contributions

  1. Equivalence proof: Shows DPO optimizes the same objective as RLHF
  2. Completeness: Proves any reward function class can be represented with their reparameterization
  3. Stability analysis: Explains why actor-critic methods (like PPO) can be unstable due to high-variance gradients

Significance

This work represents a paradigm shift in preference learning by showing that the seemingly necessary complexity of RLHF can be completely avoided. DPO makes training language models from human preferences accessible to a much broader range of practitioners while providing better or equivalent results.

What makes this particularly impactful is that it challenges a fundamental assumption in the field - that you need reinforcement learning to learn from preferences - and provides both theoretical justification and empirical validation for a much simpler alternative.


Constitutional AI

paper

blog

Quick Summary


Toy Models of Superposition

blog

Quick Summary


Towards Monosemanticity: Decomposing Language Models With Dictionary Learning

paper

Quick Summary


PaLM 2

paper

  • Improved multilingual capabilities
  • Enhanced reasoning
Quick Summary

Core Contribution

PaLM 2 achieves better performance than its much larger predecessor while being significantly more compute-efficient. This challenges the “bigger is always better” paradigm in Language Modeling.

Key Technical Insights

1. Scaling Laws Validation

  • Independently confirms Hoffmann et al.’s findings that model parameters (N) and training tokens (D) should scale roughly 1:1
  • This differs from earlier scaling approaches that prioritized model size over data

2. Three-Pronged Improvement Strategy

  • Better data mixture: More multilingual, diverse, and higher-quality training data
  • Improved architecture: Uses a mixture of training objectives (not just standard Language Modeling)
  • Compute-optimal scaling: Smaller model trained on more tokens rather than just scaling up parameters

3. Multilingual Excellence

  • Strong performance across hundreds of languages
  • Passes advanced language proficiency exams (C2 level) in multiple languages
  • Significant improvements on translation tasks

Performance Highlights

  • Outperforms the much larger PaLM 540B on most benchmarks
  • Achieves state-of-the-art results on reasoning tasks (78.1% on BIG-Bench Hard)
  • Strong coding capabilities across multiple programming languages
  • Reduced memorization compared to PaLM

Responsible AI Focus

  • Extensive evaluation of potential harms and biases across languages
  • Analysis of memorization and privacy implications
  • Inference-time toxicity control mechanisms

What makes this particularly interesting is that it demonstrates that careful data curation, architectural improvements, and compute-optimal training can be more effective than simply scaling up model size - a finding with significant implications for the field’s resource requirements and accessibility.


LAION-5B (LAION)

I was conflicted about whether I should put it here or not. But this is one of the best works that made advancements in multi-modality possible.

paper

  • Large-scale image-text dataset
  • Enabled better multimodal training
Quick Summary

This paper introduces LAION-5B, a massive open dataset containing 5.85 billion image-text pairs designed for training large-scale multimodal models like CLIP and text-to-image generators. Here’s the high-level picture:

Key Contribution

The authors address a critical bottleneck in multimodal AI research: while models like CLIP and DALL-E demonstrated the power of training on billions of image-text pairs, the datasets used were proprietary and unavailable to the broader research community. LAION-5B democratizes access to large-scale multimodal training data.

Dataset Composition

  • 2.32B English image-text pairs
  • 2.26B multilingual pairs (100+ languages)
  • 1.27B “unknown language” pairs (short-form text, product names, etc.)

Collection Methodology

  1. Started with Common Crawl web archives
  2. Extracted images with alt-text from HTML
  3. CLIP-filtered pairs using cosine similarity thresholds (0.28 for English, 0.26 for others)
  4. Added safety tags for NSFW content, watermarks, and inappropriate material

Validation Results

The authors demonstrate LAION’s utility by successfully reproducing CLIP model performance and training state-of-the-art text-to-image models (Stable Diffusion, GLIDE variants).

Significance

This represents the first openly available dataset at the scale needed for training foundation multimodal models, potentially accelerating research in vision-language AI while enabling transparency and bias auditing.


LIMA

paper

Demonstrated efficiency of small high-quality datasets 1,000 examples for alignment

Quick Summary

This paper presents LIMA, a striking demonstration that effective language model alignment can be achieved with remarkably little data. The core finding challenges conventional wisdom about the scale of instruction tuning needed for high-quality conversational AI.

Key Contribution

The authors propose the Superficial Alignment Hypothesis: that a model’s knowledge and capabilities are learned almost entirely during pretraining, while alignment primarily teaches the model which response format and style to use when interacting with users.

Experimental Design

  • Started with LLaMa 65B (pretrained base model)
  • Fine-tuned on only 1,000 carefully curated prompt-response pairs
  • No reinforcement learning from human feedback (RLHF)
  • No massive instruction datasets (unlike typical approaches using millions of examples)

Dataset Composition (1,000 examples total)

  • 750 examples from community Q&A (Stack Exchange, wikiHow, Reddit)
  • 250 manually authored examples by the research team
  • Emphasis on quality and diversity over quantity

Results

Human preference study across 300 test prompts showed LIMA:

  • Outperforms DaVinci003 (RLHF-trained) and Alpaca 65B (52K examples)
  • Produces equivalent or better responses than GPT-4 in 43% of cases
  • 58% win/tie rate against Bard, 65% against DaVinci003

Key Insights

  1. Quality » Quantity: Diminishing returns from scaling data without improving diversity/quality
  2. Emergent capabilities: Zero-shot dialogue ability that improves dramatically with just 30 dialogue examples
  3. Pretraining power: Most knowledge acquisition happens during pretraining, not instruction tuning

This work has profound implications for understanding what makes language models helpful and could democratize access to high-quality conversational AI by dramatically reducing the data requirements for alignment.


Mamba

https://tridao.me/blog/

paper

  • State space model for sequence modeling
  • Linear scaling with sequence length
Quick Summary

This paper introduces Mamba, a novel neural network architecture that aims to replace Transformers for sequence modeling tasks. Here’s the high-level story:

The Core Problem

Transformers dominate modern AI but have a fundamental limitation: their attention mechanism scales quadratically with sequence length, making them computationally expensive for long sequences (think processing entire books, long DNA sequences, or extended audio).

The Proposed Solution

The authors develop Selective State Space Models (SSMs) - a new approach that:

  • Scales linearly with sequence length (much more efficient)
  • Introduces a novel “selection mechanism” that allows the model to selectively focus on or ignore parts of the input sequence
  • Achieves performance comparable to Transformers while being significantly faster

Key Innovation: Selection Mechanism

Traditional SSMs are “linear time-invariant” - they process all inputs the same way. Mamba’s breakthrough is making the model parameters input-dependent, allowing it to:

  • Remember important information indefinitely
  • Forget irrelevant details
  • Adapt its behavior based on context

Empirical Results

The paper demonstrates that Mamba:

  • Matches or exceeds Transformer performance on Language Modeling
  • Handles sequences up to 1 million tokens
  • Achieves 5× higher inference throughput than Transformers
  • Works well across multiple domains (language, DNA, audio)

This represents a significant step toward more efficient sequence models that could handle much longer contexts than current Transformers. The mathematical foundation combines classical control theory (state space models) with modern deep learning innovations.


LLaVA (Visual Instruction Tuning)

paper

  • Released in April 2023 LLaVA was among the first vision-language models created using visual instruction tuning
  • Combined vision encoders with language models
  • Pioneered efficient visual instruction tuning
  • Set foundation for open-source multimodal models
Quick Summary

This paper introduces visual instruction tuning - the first attempt to extend instruction-following capabilities from language-only models to multimodal vision-language tasks. The key contributions are:

Core Innovation: Using GPT-4 to automatically generate multimodal instruction-following data by converting image-text pairs into conversational format, then training a model that connects a vision encoder (CLIP) with a language model (Vicuna).

Technical Approach:

  • A simple but effective architecture: CLIP vision encoder → linear projection → LLM
  • Two-stage training: (1) feature alignment pre-training, (2) end-to-end instruction tuning
  • 158K generated instruction-following samples across conversations, detailed descriptions, and complex reasoning

Key Results:

  • Achieves 85.1% relative performance compared to GPT-4 on synthetic benchmarks
  • Sets new SOTA on ScienceQA (92.53%) when combined with GPT-4
  • Demonstrates strong generalization to unseen visual concepts and tasks

Significance: This work essentially brought the “ChatGPT moment” to multimodal AI by showing that instruction tuning - which revolutionized language models - could be successfully adapted to vision-language tasks using generated data rather than expensive human annotation.

I’m ready to dive deeper into any aspect you’d like to explore - whether that’s the mathematical formulations, training procedures, data generation pipeline, or architectural choices. What interests you most about this approach?


Claude 1/Claude 2

  • Released in March 2023 (Claude 1) and July 2023 (Claude 2)
  • Focused on constitutional AI approach
  • Enhanced safety and alignment
  • Specialized in long-form content generation

Gemini

paper

  • Announced initially in May 2023, fully released in December Described as “a family of multimodal large language models developed by Google DeepMind, and the successor to LaMDA and PaLM 2”
  • Designed from the ground up as a multimodal model
  • Positioned as Google’s answer to GPT-4
Quick Summary

This is Google’s technical report introducing Gemini, a family of multimodal AI models that can process and understand text, images, audio, and video simultaneously. The paper presents three model sizes:

  • Gemini Ultra: The most capable model for complex reasoning tasks
  • Gemini Pro: Balanced performance and efficiency for scalable deployment
  • Gemini Nano: Optimized for on-device applications

Key Highlights:

Breakthrough Performance: Gemini Ultra achieves state-of-the-art results on 30 of 32 benchmarks tested, becoming the first model to surpass human expert performance on MMLU (90.04% vs 89.8% human expert threshold).

Native Multimodality: Unlike models that combine separate systems, Gemini is trained from the ground up to understand multiple modalities together, enabling sophisticated cross-modal reasoning.

Technical Innovation: Built on enhanced Transformer architecture, trained on Google’s TPU infrastructure with novel approaches to handle massive scale (97% training efficiency despite unprecedented resource usage).

Responsible Deployment: Extensive safety evaluations, red-teaming, and responsible AI practices integrated throughout development.

The paper is quite comprehensive at 90+ pages, covering everything from architectural details and training infrastructure to extensive benchmarking and safety considerations.


Qwen

paper

Quick Summary

This paper introduces QWEN, a comprehensive series of large language models developed by Alibaba’s Qwen Team. Here’s the high-level picture:

What they built: A family of language models ranging from 1.8B to 14B parameters, including:

  • Base pretrained models (QWEN)
  • Chat-aligned models (QWEN-CHAT)
  • Specialized variants for coding (CODE-QWEN) and mathematics (MATH-QWEN)

Key contributions:

  1. Scale & Performance: Models trained on up to 3 trillion tokens, demonstrating competitive performance against much larger models
  2. Multilingual Focus: Strong emphasis on Chinese-English bilingual capabilities with an optimized tokenizer
  3. Specialized Training: Domain-specific fine-tuning for coding and mathematical reasoning
  4. Comprehensive Alignment: Full pipeline from supervised fine-tuning (SFT) to reinforcement learning from human feedback (RLHF)

Technical highlights: The paper covers the complete model development lifecycle - from pretraining data curation and architectural choices to alignment techniques and specialized model variants. They achieve impressive results, with QWEN-14B outperforming many larger open-source models.

What makes this particularly interesting is their systematic approach to building not just one model, but an entire ecosystem of specialized variants, all while maintaining strong multilingual capabilities.

What aspects of this work would you like to dive deeper into? I’m ready to explore the mathematical foundations, training methodologies, or any specific techniques that caught your attention!


Qwen-VL

paper

Quick Summary

This paper introduces Qwen-VL, a series of large-scale vision-language models that can process both images and text. The key contribution is creating models that go beyond basic image captioning and visual question answering to include fine-grained capabilities like:

  • Visual grounding (localizing objects with bounding boxes)
  • Text reading (OCR capabilities)
  • Multi-image conversations
  • Multilingual support (English and Chinese)

Architecture Overview:

  • Built on the Qwen-7B language model foundation
  • Uses a Vision Transformer (ViT) as the visual encoder
  • Introduces a novel “position-aware vision-language adapter” that compresses visual features while preserving spatial information
  • Total model size: ~9.6B parameters

Training Pipeline: The authors use a carefully designed 3-stage training approach:

  1. Pre-training on 1.4B image-text pairs (frozen LLM)
  2. Multi-task pre-training on 7 different vision-language tasks simultaneously
  3. Supervised fine-tuning for instruction-following and chat capabilities

Key Results: Qwen-VL achieves state-of-the-art performance across multiple benchmarks compared to similar-scale models, particularly excelling in text-oriented tasks and fine-grained visual understanding.


Phi-1

paper

Quick Summary

This paper introduces phi-1, a remarkably compact 1.3B parameter language model for code generation that achieves impressive performance despite being orders of magnitude smaller than competing models. The key insight is that data quality trumps data quantity - they achieved 50.6% pass@1 accuracy on HumanEval and 55.5% on MBPP using only 7B tokens of carefully curated “textbook quality” data.

Core Innovation: Instead of following traditional scaling laws (bigger models + more data = better performance), they focused on three high-quality datasets:

  1. Filtered code from The Stack/StackOverflow (~6B tokens) using GPT-4-based quality classification
  2. Synthetic textbooks generated by GPT-3.5 (<1B tokens)
  3. Synthetic exercises for fine-tuning (~180M tokens)

Key Results: phi-1 outperforms much larger models like StarCoder (15.5B parameters, 1T tokens) while being trained 100x faster and using 100x less data.

Broader Implications: This work suggests that the “bitter lesson” of simply scaling compute might not be the only path forward - careful data curation can dramatically improve learning efficiency.


Reinforced Self-Training (ReST) for Language Modeling

paper

Quick Summary
Quick Summary


The Era of 1-bit LLMs: All Large Language Models are in 1.58 Bits

paper

Quick Summary
Quick Summary


2024: Efficiency and Performance

It’s June 2025 currently while I am writing this, and I cannot say for certain if the innovations mentioned in this and the next year will have huge impacts in the future, I just went with the papers and models that have caught “attention” in this time period. As well as ideas that I found unconventional and interesting.

Gemma

paper

Quick Summary

Gemma: Open Models Based on Gemini Research and Technology introduces a family of open-source language models derived from Google’s Gemini research. This represents a significant contribution to the open AI ecosystem, as it makes state-of-the-art capabilities more accessible to researchers and developers.

Key Contributions:

  • Two model sizes: 2B and 7B parameters, designed for different computational constraints
  • Dual releases: Both pre-trained base models and instruction-tuned chat variants
  • Strong performance: Outperforms similarly-sized open models on 11 out of 18 benchmarks
  • Responsible AI focus: Comprehensive safety evaluations and responsible deployment practices

Architecture Highlights:

  • Built on transformer decoder architecture with modern improvements
  • Uses RoPE embeddings for positional encoding
  • GeGLU activations instead of standard ReLU
  • Multi-query attention for the 2B model, multi-head for 7B
  • Trained on up to 6T tokens of primarily English text

Training Pipeline:

  1. Pre-training on web documents, mathematics, and code
  2. Supervised Fine-Tuning (SFT) on instruction-response pairs
  3. RLHF using human preference data

Notable Results:

  • Gemma 7B achieves 64.3% on MMLU and 44.4% on MBPP
  • Strong performance on mathematics (46.4% on GSM8K) and coding tasks
  • Comprehensive safety evaluations show competitive performance on responsibility benchmarks


Gemma 2

Quick Summary

This paper introduces Gemma 2, Google DeepMind’s next-generation family of open language models ranging from 2B to 27B parameters. Here’s the key story:

Core Innovation: Knowledge Distillation at Scale

The paper’s main contribution is demonstrating that knowledge distillation - where smaller “student” models learn from larger “teacher” models - can dramatically improve performance when applied at massive scale (training on 50× more tokens than typically considered optimal).

Key Technical Advances

  • Architectural improvements: Interleaving local sliding window attention with global attention, grouped-query attention (GQA), and logit soft-capping
  • Training methodology: Using distillation instead of standard next-token prediction for the 2B and 9B models
  • Responsible deployment: Extensive safety evaluations and responsible AI toolkit development

Performance Highlights

  • The models achieve state-of-the-art performance for their size class
  • Gemma 2-27B competes with models 2-3× larger (like LLaMA-3 70B)
  • Strong results on the LMSYS Chatbot Arena, with Gemma 2-27B ranking higher than LLaMA-3 70B

Broader Impact

The paper provides evidence that smaller, more efficiently trained models can challenge the “bigger is always better” paradigm in LLMs, which has important implications for democratizing access to capable AI systems.


Chatbot Arena: An Open Platform for Evaluating LLMs by Human Preference

paper

Quick Summary

This paper introduces Chatbot Arena, a crowdsourced platform for evaluating Large Language Models (LLMs) through human preferences rather than traditional static benchmarks. Here are the key contributions:

Core Innovation: The platform uses a “battle” format where users interact with two anonymous LLMs simultaneously, then vote for which response they prefer. This creates a live, dynamic evaluation system that captures real-world usage patterns.

Scale & Impact: Since April 2023, they’ve collected over 240K votes from 90K+ users across 100+ languages, making it one of the most referenced LLM leaderboards in the field.

Mathematical Framework: The paper employs sophisticated statistical methods to convert pairwise comparisons into reliable rankings:

  • Bradley-Terry model for estimating win probabilities
  • Active sampling algorithms to efficiently select model pairs for comparison
  • Confidence intervals and anomaly detection for robust evaluation

Key Findings:

  • Crowdsourced votes show high agreement (72-83%) with expert evaluations
  • The diverse, user-generated prompts effectively discriminate between model capabilities
  • Their ranking system provides statistically valid confidence intervals for model performance

Why It Matters: This addresses critical limitations of static benchmarks (contamination, lack of human alignment, limited diversity) by creating a continuously updating, human-preference-based evaluation system that better reflects real-world LLM usage.


TinyLlama: An Open-Source Small Language Model

paper

Quick Summary

This paper presents TinyLlama, a remarkably compact 1.1B parameter language model that challenges conventional wisdom about the relationship between model size and performance. The key insight is exploring what happens when you train a small model on far more data than traditional scaling laws suggest - specifically training on up to 3 trillion tokens (later reduced to 2T in v1.1).

Core Contributions:

  • Architecture: Built on Llama 2’s foundation but optimized for efficiency with techniques like FlashAttention and grouped-query attention
  • Training Strategy: Demonstrates that smaller models can achieve competitive performance when trained on significantly more data than scaling laws recommend
  • Multi-stage Training: Introduces a three-phase approach (basic pretraining → domain-specific continual pretraining → cooldown) that creates specialized variants
  • Performance: Outperforms comparable models like OPT-1.3B and Pythia-1.4B across multiple benchmarks despite being smaller

Key Insight: Rather than following compute-optimal scaling (Chinchilla scaling laws), they pursue inference-optimal scaling - training smaller models longer to achieve better performance per parameter during deployment.

The work is particularly valuable for democratizing language model research, enabling applications on resource-constrained devices, and providing a strong foundation for experimentation.


MordernBert

paper

Quick Summary

This paper introduces ModernBERT, a significant modernization of the classic BERT encoder architecture. The key insight is that while decoder-only models like GPT have seen tremendous advances, encoder-only models have remained largely stagnant since BERT’s original release in 2019.

Core Contributions:

  1. Architectural Modernization: Incorporates proven techniques from recent transformer research (RoPE positional embeddings, GeGLU activations, alternating local/global attention)
  2. Scale & Data: Trained on 2 trillion tokens with modern data mixtures including code
  3. Hardware-Aware Design: Optimized for inference efficiency on common GPUs
  4. Long Context: Native 8192 sequence length (vs BERT’s 512)

Key Results:

  • State-of-the-art performance across classification, retrieval, and code tasks
  • ~2x faster inference than previous long-context encoders
  • First encoder to beat DeBERTaV3 on GLUE since 2021
  • Strong performance on both single-vector and multi-vector retrieval

Why This Matters: Encoders remain crucial for production systems doing retrieval, classification, and RAG pipelines where efficiency matters more than generation capability. ModernBERT shows there’s still significant room for improvement in this “mature” architecture family.


Jamba: A Hybrid Transformer-Mamba Language Model

paper

Quick Summary

This paper introduces Jamba, a novel hybrid architecture that combines three key components:

  1. Transformer layers (the standard attention mechanism we know)
  2. Mamba layers (a recent state-space model that’s more memory-efficient)
  3. Mixture-of-Experts (MoE) (to scale model capacity while keeping compute manageable)

Key Innovation

Instead of using pure Transformer or pure Mamba architectures, Jamba interleaves these different layer types in a flexible pattern. The released model uses a 1:7 ratio (1 attention layer for every 7 Mamba layers) and achieves:

  • 52B total parameters but only 12B active parameters
  • 256K token context length support
  • 8x smaller KV cache compared to vanilla Transformers
  • 3x better throughput than Mixtral on long contexts
  • Fits in a single 80GB GPU

The Core Problem It Solves

Transformers struggle with long contexts due to quadratic memory scaling and large KV caches. Mamba is more efficient but historically underperforms Transformers. Jamba gets the best of both worlds by combining them strategically.

Particularly Interesting Finding

The paper shows that pure Mamba struggles with in-context learning (following formats in few-shot examples), but adding just a few attention layers restores this capability - suggesting attention mechanisms play a crucial role in pattern copying and format adherence.


Claude 3

Technical Report

  • Multi-modal understanding
  • Tool use capabilities
  • Advanced reasoning
  • Constitutional AI improvements
Quick Summary


LLaMA 3

https://github.com/naklecha/llama3-from-scratch

paper

Quick Summary

This is Meta’s comprehensive technical report on Llama 3, their latest family of foundation models. Here’s a high-level summary:

What They Built

  • Three model sizes: 8B, 70B, and 405B parameters
  • Flagship model: Llama 3 405B - a dense transformer with 128K context window
  • Multimodal extensions: Vision, video, and speech capabilities (experimental)
  • Performance: Competitive with GPT-4, Claude 3.5 Sonnet on many benchmarks

Key Technical Contributions

Scale & Data:

  • 405B model trained on 15.6T tokens (vs 1.8T for Llama 2)
  • 50× more compute than largest Llama 2 model
  • Extensive data curation and quality filtering pipelines

Infrastructure Innovation:

  • 4D parallelism for training at 16K GPU scale
  • Novel pipeline parallelism improvements
  • FP8 quantization for efficient inference

Safety & Alignment:

  • Comprehensive safety evaluation across capabilities
  • Llama Guard 3 for system-level safety
  • Extensive red teaming and adversarial testing

Mathematical Foundation

The paper is built on established scaling laws but pushes them to new extremes, with careful attention to compute-optimal training and the tension between model size and training duration.


Claude 3

Opus, Sonnet, and Haiku variants Improved reasoning and multimodal capabilities

Gemini 1.5

paper

Quick Summary

This paper introduces Gemini 1.5 Pro and Gemini 1.5 Flash - a new generation of multimodal AI models that represent a major leap in long-context understanding. The standout achievement is extending context windows from the typical 32K-200K tokens to up to 10 million tokens across text, images, video, and audio modalities.

Key Innovations:

  • Architecture: Gemini 1.5 Pro uses a sparse mixture-of-experts (MoE) Transformer, while Flash is a distilled dense model
  • Unprecedented Scale: Can process ~7 million words, 107 hours of audio, or 10.5 hours of video in a single context
  • Multimodal Excellence: Near-perfect recall (>99%) on “needle-in-haystack” tasks across all modalities
  • Practical Capabilities: Learn new languages from single grammar books, analyze entire codebases, reason over hour-long videos

Performance Highlights:

  • Outperforms Gemini 1.0 Ultra on most benchmarks despite using less training compute
  • Achieves state-of-the-art on many multimodal reasoning tasks
  • Demonstrates remarkable in-context learning (e.g., translating Kalamang, a language with <200 speakers, from documentation alone)

The paper also includes extensive safety evaluations and introduces novel benchmarks for long-context evaluation, addressing a key challenge in evaluating such capable models.

Mathematical/Technical Depth: The paper contains rich technical content around scaling laws, architectural innovations, and evaluation methodologies that we could dive deep into.


Qwen 2

Quick Summary

This paper introduces Qwen2, a comprehensive family of large language models ranging from 0.5B to 72B parameters, including both dense models and a Mixture-of-Experts (MoE) variant. Here are the key highlights:

Main Contributions:

  • Model Family: Five model sizes (0.5B, 1.5B, 7B, 57B-A14B MoE, 72B) designed for different deployment scenarios
  • Performance: The flagship Qwen2-72B achieves strong results across benchmarks (84.2 MMLU, 64.6 HumanEval, 89.5 GSM8K)
  • Multilingual: Supports ~30 languages with robust capabilities
  • Long Context: Extended context length up to 131K tokens using YARN and Dual Chunk Attention

Technical Innovations:

  • Architecture: Grouped Query Attention (GQA) for efficient inference
  • MoE Design: Fine-grained experts with shared + routing-specific expert structure
  • Training: 7T tokens for dense models, enhanced data quality and distribution
  • Post-training: Scalable alignment with minimal human annotation using automated synthesis

Key Strengths:

  • Outperforms most open-weight models including Qwen1.5
  • Competitive with proprietary models across diverse benchmarks
  • Strong performance in coding, mathematics, and reasoning tasks
  • Comprehensive safety and contamination analysis

The paper represents a significant step forward in open-weight language models, with particular attention to practical deployment considerations and rigorous evaluation methodology.


phi-2/phi-3

Small but powerful models High performance with limited training data

Quick Summary


OpenAI o1

First specialized reasoning model Advanced mathematical problem-solving

Quick Summary


RSO (Reinforced Self-training with Online feedback)

  • Self-improvement through AI evaluation
  • Reduced human annotation needs
Quick Summary


SPIN (Self-Played Improvement Narration)

  • Self-correction capabilities
  • Improved factual accuracy
Quick Summary


DBRX

blog

Quick Summary


FlashAttention-3: Fast and Accurate Attention with Asynchrony and Low-precision

paper

Quick Summary


Qwen 2.5 (Alibaba)

  • Released in September 2024 as “the latest addition to the Qwen family,” which the developers called “the largest opensource release in history”
  • Specialized variants for coding and mathematics
  • Sizes ranging from 1.5B to 72B parameters
  • Strong multilingual capabilities
Quick Summary


DeepSeek 2.5 (DeepSeek)

  • Released in September 2024 combining “DeepSeek-V2-Chat and DeepSeek-Coder-V2-Instruct” as an “upgraded version”
  • Competitive code generation capabilities
  • Cost-effective alternative to larger models
  • 128K token context window
Quick Summary


Claude 3.5 Sonnet (Anthropic)

  • Released in October 2024 featuring improved performance “in undergraduate knowledge, graduate-level reasoning, general reasoning, and code generation”
  • Advanced reasoning and coding capabilities
  • Introduces Artifacts for interactive content creation
  • Significant improvements over Claude 3 Opus
Quick Summary


DeepSeek-R1 (DeepSeek)

  • Specialized reasoning model released in December 2024
  • Focus on mathematical and logical reasoning
  • Designed to compete with OpenAI’s o1
  • Significantly faster inference than o1
Quick Summary


Phi 3

paper

Quick Summary

This paper introduces the Phi-3 family of compact yet highly capable language models, with the flagship phi-3-mini (3.8B parameters) achieving performance competitive with much larger models like Mixtral 8x7B and GPT-3.5. The key breakthrough is that phi-3-mini can run locally on a phone while achieving 69% on MMLU and 8.38 on MT-bench.

Key Innovations from phi-1:

  • Massive scale-up: From 1.3B to 3.8B parameters, trained on 3.3T tokens (vs 7B tokens for phi-1)
  • Enhanced data recipe: Evolved the “textbook quality” approach with more sophisticated filtering and synthetic data generation
  • Model family: phi-3-small (7B), phi-3-medium (14B), and phi-3.5 variants including MoE and Vision models
  • Production ready: Full safety alignment, chat formatting, and mobile deployment

The “Data Optimal” Philosophy: Rather than following traditional compute-optimal scaling laws, they focus on curating the highest quality training data for a given model size - essentially asking “what’s the best data diet for a 4B parameter model?” rather than “how big should we make the model?”

Remarkable Results: A 3.8B model that fits on a phone outperforming models 10-25x larger, suggesting we may be far from the efficiency frontier that traditional scaling laws suggest.


Phi 4

paper

Quick Summary

This paper introduces Phi-4, a 14-billion parameter language model that achieves remarkable performance through a data-centric approach rather than simply scaling model size. Here are the key highlights:

Core Innovation: Quality over Scale

  • Central Philosophy: Strategic use of high-quality synthetic data throughout training, moving beyond traditional web-scraped datasets
  • Architecture: 14B parameters with minimal changes from Phi-3, proving that data quality can rival compute scaling
  • Performance: Outperforms much larger models (even its teacher GPT-4o) on STEM reasoning tasks like GPQA and MATH

Three Pillars of Development

  1. Synthetic Data Generation: ~400B tokens using diverse techniques including multi-agent prompting, self-revision workflows, and instruction reversal
  2. Curated Organic Data: Meticulous filtering of web content, books, and code repositories to extract high-reasoning seeds
  3. Advanced Post-Training: Novel “Pivotal Token Search” (PTS) method for DPO that targets the most impactful tokens in reasoning chains

Standout Results

  • Fresh Evaluation: Strong performance on November 2024 AMC-10/12 math competitions (completely contamination-proof)
  • STEM Excellence: Surpasses teacher model GPT-4o on graduate-level STEM (GPQA) and math competition problems (MATH)
  • Efficiency: Achieves frontier-model reasoning capabilities at a fraction of the computational cost

Mathematical Innovation

The paper introduces Pivotal Token Search, a fascinating approach that identifies tokens with the highest impact on solution success probability, creating more targeted preference optimization data.

What would you like to explore first? I’d be happy to dive deeper into:

  • The mathematical formulation of Pivotal Token Search
  • The synthetic data generation techniques and their theoretical foundations
  • The training dynamics and curriculum design
  • The contamination-proof evaluation methodology
  • Any specific technical aspects that caught your attention


Self-Play Fine-Tuning Converts Weak Language Models to Strong Language Models

paper

Quick Summary


2025

Gemma 3

paper

Quick Summary

What it is: Gemma 3 represents a significant evolution in the Gemma family, introducing multimodal capabilities (vision + text), extended context length (128K tokens), and improved multilingual support while maintaining the lightweight, open-model philosophy.

Key Technical Innovations:

  • Hybrid attention architecture: A 5:1 ratio of local-to-global attention layers to manage long context memory efficiently
  • Multimodal integration: SigLIP vision encoder with Pan & Scan method for flexible image resolutions
  • Enhanced post-training: Novel distillation and reinforcement learning techniques (BOND, WARM, WARP)

Model Sizes: 1B, 4B, 12B, and 27B parameters, designed for consumer hardware deployment

Performance Highlights: The 27B instruction-tuned model achieves an ELO score of 1338 on Chatbot Arena, ranking among top-10 models while being significantly smaller than competitors like LLaMA 3 405B.

Mathematical Focus Areas: The paper contains rich material on attention mechanisms, knowledge distillation formulations, memory optimization techniques, and scaling laws for multimodal training.

This paper offers excellent opportunities to explore modern transformer architectures, efficient attention patterns, multimodal fusion techniques, and post-training optimization methods.


Llama 4

Qwen2.5

Quick Summary

This paper introduces Qwen2.5, a comprehensive series of large language models representing a significant advancement over previous iterations. Here are the key highlights:

Core Improvements

  • Massive data scaling: Pre-training dataset expanded from 7 trillion to 18 trillion tokens
  • Enhanced post-training: Sophisticated supervised fine-tuning with 1M+ samples plus multi-stage reinforcement learning (DPO + GRPO)
  • Extended capabilities: Generation length increased from 2K to 8K tokens, better structured data handling

Model Family

  • Open-weight models: 0.5B, 1.5B, 3B, 7B, 14B, 32B, and 72B parameters
  • Proprietary MoE variants: Qwen2.5-Turbo and Qwen2.5-Plus for API services
  • Long-context version: Qwen2.5-Turbo supports up to 1M tokens

Performance Achievements

  • Qwen2.5-72B-Instruct matches Llama-3-405B-Instruct performance while being ~5× smaller
  • Strong improvements across mathematics, coding, reasoning, and multilingual tasks
  • Competitive with GPT-4o-mini and GPT-4o for the MoE variants

Technical Innovations

  • Progressive context length scaling during training
  • Advanced long-context techniques (YARN + DCA)
  • Two-stage reinforcement learning (offline + online RL)
  • Sophisticated data filtering using Qwen2-Instruct models

The paper demonstrates how careful scaling of both data and training techniques can achieve remarkable efficiency gains, making state-of-the-art performance accessible with significantly fewer parameters.


Qwen 2.5-1M

paper

Quick Summary


Qwen2.5-Omni

paper

Quick Summary


Qwen 3

paper

Quick Summary


Grok

  • Open-source model
  • 314B parameters
Quick Summary

</details>

Pixtral

paper

  • Multimodal capabilities
  • 12B parameters
Quick Summary


Large Language Diffusion Models

paper

Quick Summary


https://hkunlp.github.io/blog/2025/dream/

https://arxiv.org/pdf/2502.09992

RLVR

Kimi AI

Talk about optimizers here, Muon and stuff

https://magazine.sebastianraschka.com/p/the-big-llm-architecture-comparison

It’s all about DeepSeek

https://www.alphaxiv.org/abs/2505.09343

This whole section is dedicated just to the geniuses that are DeepSeek

Consider reading all their paper from this list https://huggingface.co/collections/Presidentlin/deepseek-papers-674c536aa6acddd9bc98c2ac

Quick Summary


Some Honorable blogs and mentions that I believe you should definitely check out:

blog

SELF NOTES AND MISC STUFF

Include Large Text diffusion models

Add performance charts showing scaling laws Include architecture diagrams for key innovations Create a “family tree” showing model lineage

NOTES TO SELF

  • Add a note for hardware, not in the scope of this blog but should not be ignored [DONE]
  • Quick note about benchmark, Not hear to explain these but these are the major ones that are used mostly.[DONE]
  • Under each paper, add the image of the paper with the name of the authors as well as the abstract[DONE]
  • Train a hand drawn sketch LORA in flux dev for images
  • Add a reference section in the end which redirects to the papers, Like latex reference and stuff.[DONE]

[add prerequisites section, summary section, skip to section]

A short introduction to LLMs

This part is highly influenced by this video by andrej karpathy

A paper on pretraining paper

Training

As I mentioned there are 3 kinds of architectures when it comes to LLM, hence there is a different way of training each. Even though they share few similarities. Each has a different objective. Let us begin by first understanding the most popular LLM architecture, that being the decoder only architecture.

Decoder Only

Pretraining

Step 1: Data Collection

We know Decoder based LLMs are able to answer a variety of answer to questions about science, food, mathematics, facts etc. That is because they have been trained on a huge plethora of the data.

So the first step is to collect the said data. One important thing to keep in mind is that these models are able to answer based on what they have seen. They are not performing any kind of reasoning. It is given a distribution, what is the most likely token that is to appear.

So if you want a coding LLM you will collect a lot of code related data from publically available places like github.

If you want a cooking LLM you will collected a lot of recipes and so on.

Most general purpose LLMs are trained on data collected from various sources, hence they are able to answer a lot of question.

A lot of filtering steps also goes behind it

” Garbage in, garbage out “

Most of the internet when crawled has data which looks something like this

<html>
  {add shit}
</html>

Hence it needs to be processed into a more human readable form, You can imagine how humongous of a task it must be to clean huge datasets with GBs of data.

Now there are other filterning that also needs to be done, How do you take care of profanity? What about fake news and so on

Step 2: Tokenization

{maybe talk about vocabulary and token length}

When we talked about transformers, we skipped talking about tokenization, but as it is a vital piece of LLM training. We shall spend some time talking about it here.

Sentence level tokenization

My first question was, why do we need to break down words. Why not give the entire sentence. Heck why not give the whole paragraph as an input.

While in practice it can be done, it is not wise. Because if we go back to our basic principle about LLMs.

“They are next token predictors”

So in given any large enough paragraph or even an essay. The likelihood of a sentence repeating is very low. So if we think it in terms of machines, if we transform each sentence into a token, we will have a vocabular with a lot of numbers, which do not relate to each other at all. So we can never predict what sentence will come after any given sentence.

Word level tokenization

A simple work around this seems to be, well why not just tokenize the words, instead of sentences. Because in any large enough paragraph or essay. Words repeat and they follow a logical sequence of what is to appear next. For example

“Water is ___”, if you gave me this sentence word by word, I will assume the next word is wet. Whereas if you gave me a sentence

“Water is wet, This is a debatable topic.” I will have no clue what can be said after this sentence, Maybe someone raises a point, maybe someone says something else.

So word level helps us retain the logical sequence, and words have meanings to them too. But there is still one big issue. There can be millions of words, some have way higher representation in usual text and some are highly unlikely to occur in common place.

There are words which are commonplace in one industry and rare in another.

So we will have a huge vocabulary.

If you think for a moment we may come to the conclusion that, why not use character level tokenization to solve this problem, this will reduce the vocabulary drastically.

Here the problem would lie in the fact that characters by themselves do not hold much meaning (atleast in the english lexicon)

Step 3: Training the network

Fine-Tuning

Encoder Only

Now let’s understand how a usual Encoder is trained, We will talk about BERT here

Encoder Decoder

Now let’s do the same for T5

Inference

[Expand SENTENCE PIECE WHEN IT MAKES SENE]

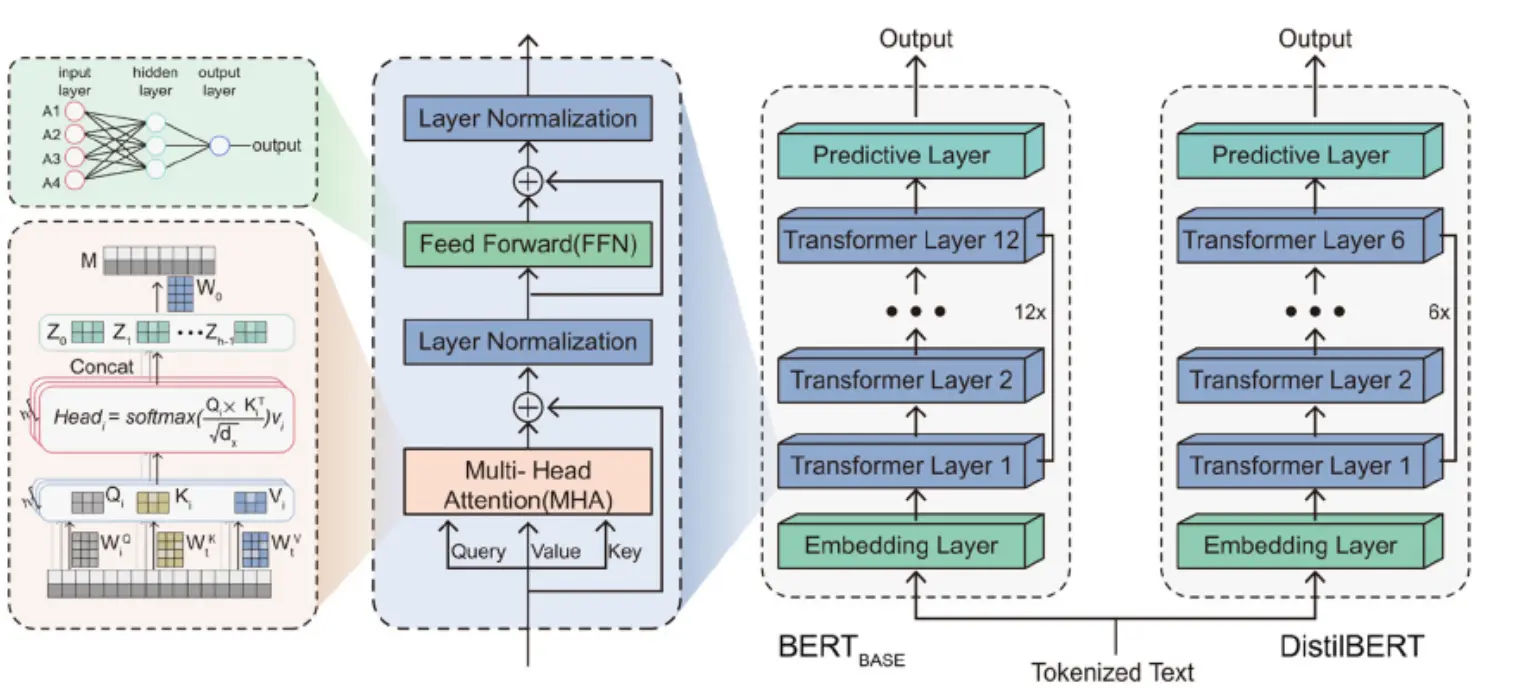
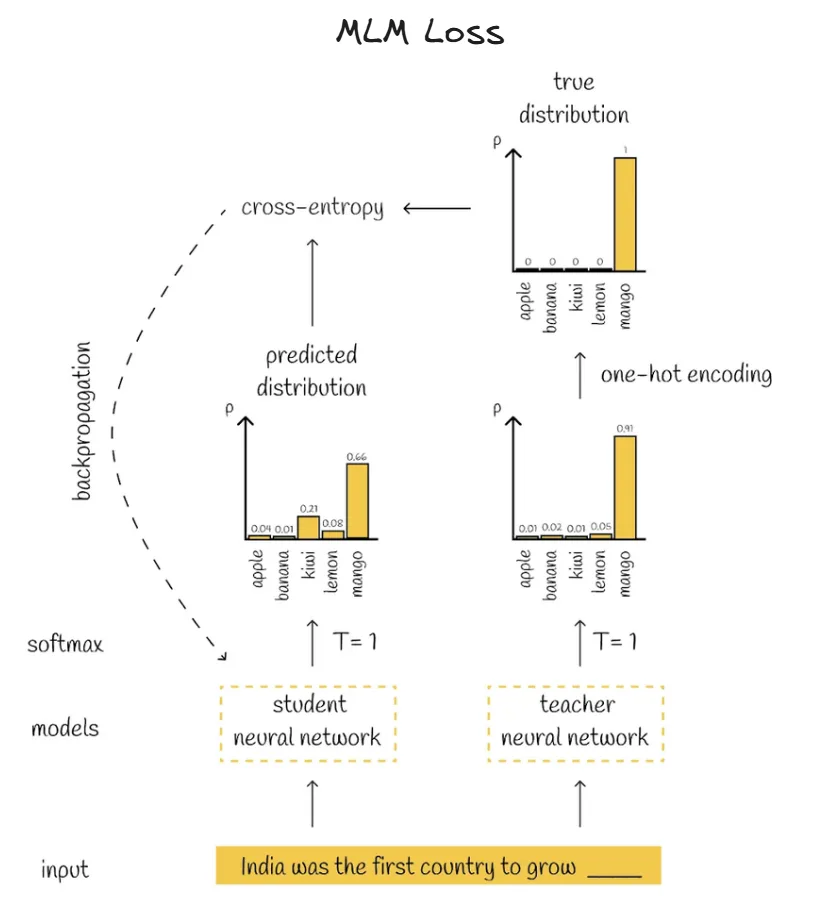
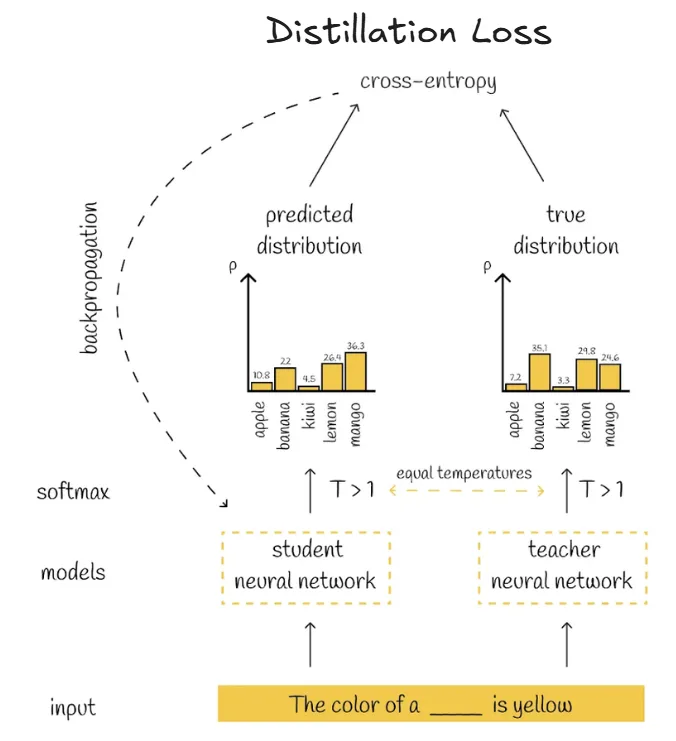
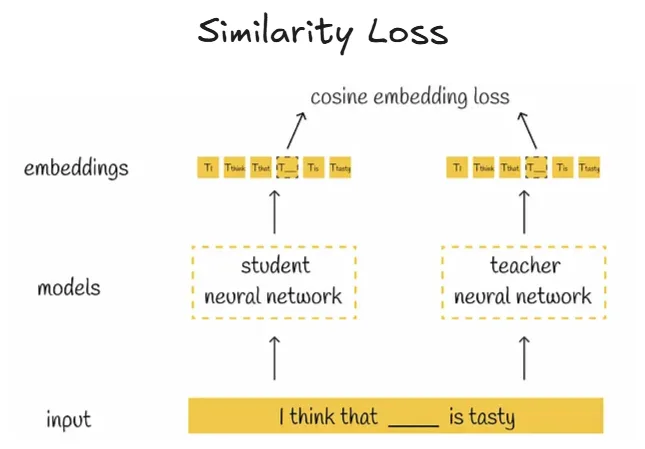
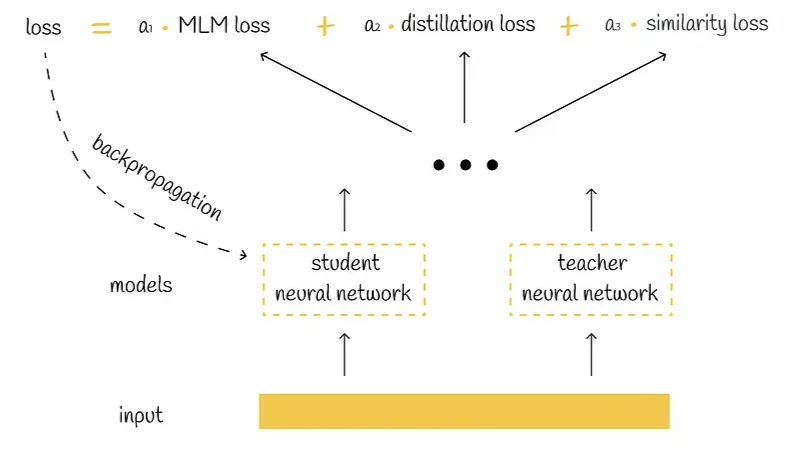
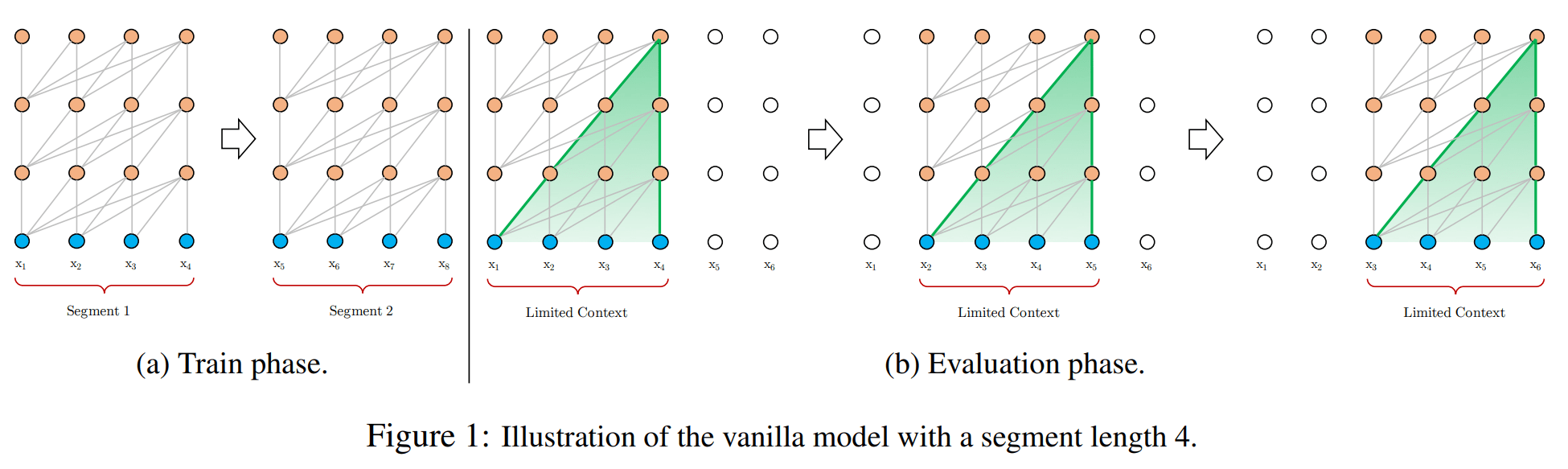
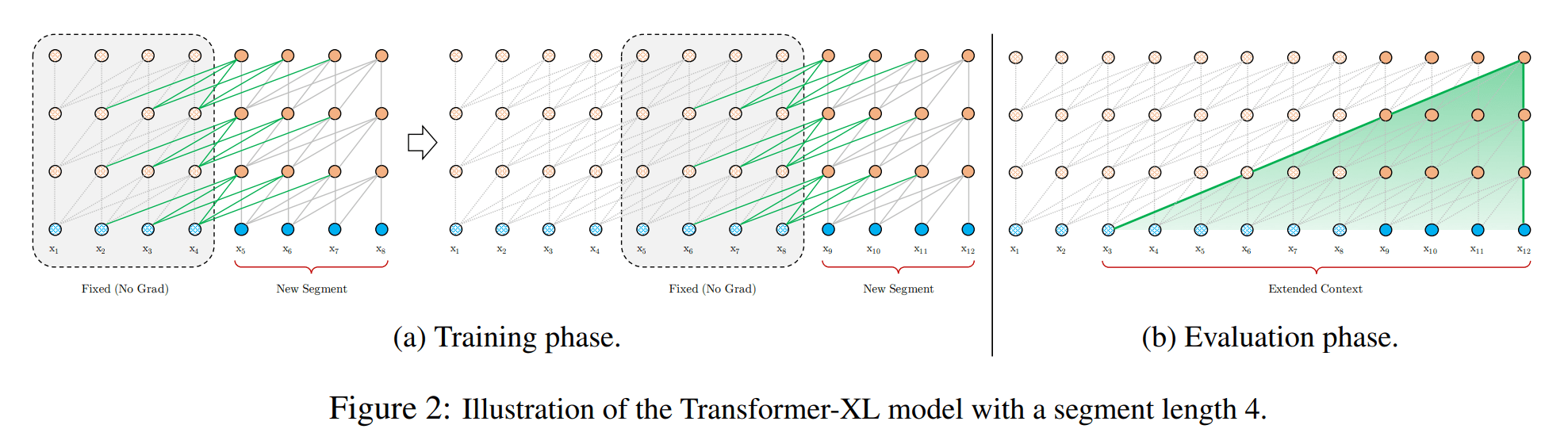
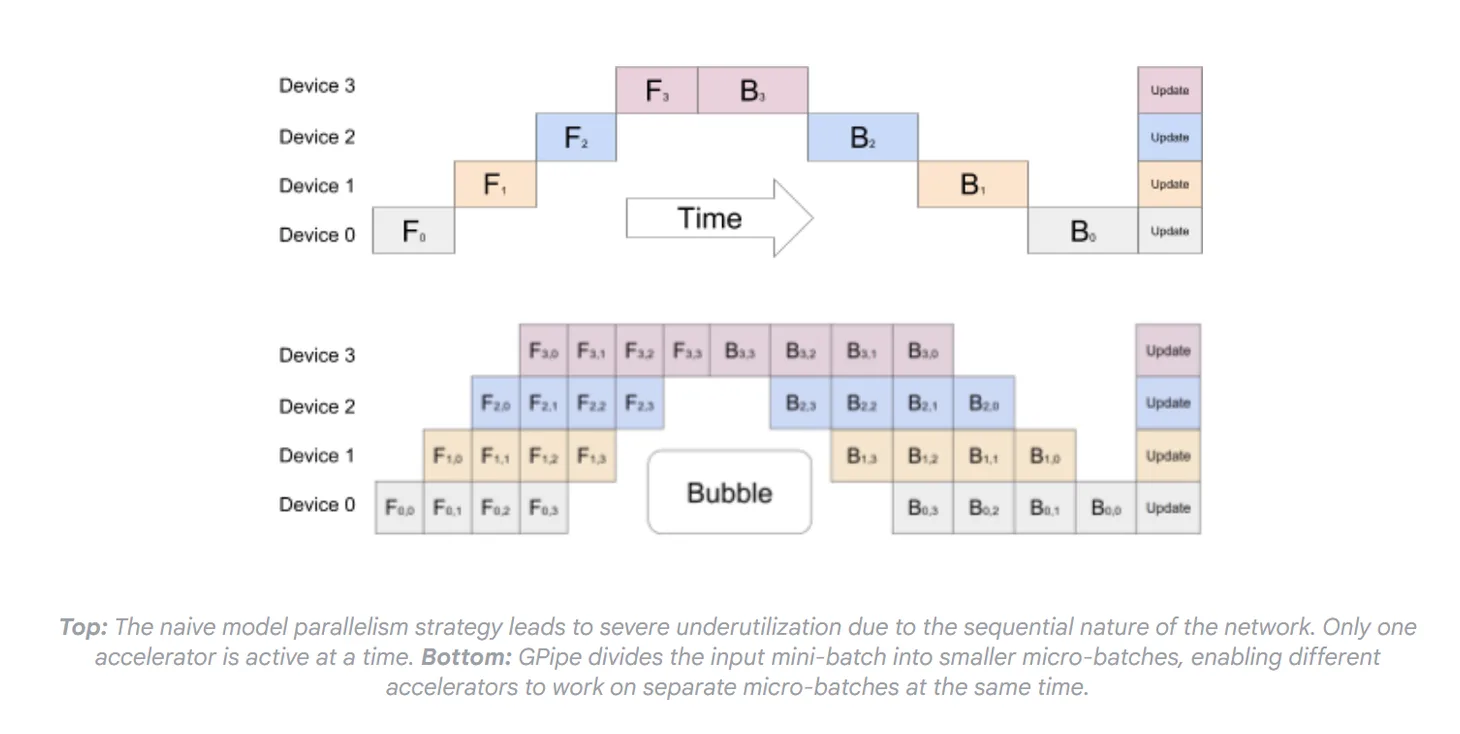
Comments